1、给你一个数组,设计一个既高效又公平的方法随机打乱这个数组(此题和洗牌算法的思想一致)
方法比较简单,基本思想是每次随机取一个数,然后把它交换到最后的位置。然后对前(n-1)个数使用递归的算法。
递归实现:
void suffle(int a[], int n)
{
if(n<=1)return;
swap(ar[n-1], a[rand()%n]);
shuffle(a,n-1);
}
非递归实现:
void suffle(int a[], int n)
{
while(n>1){
swap(a[n-1], a[rand()%n]);
n--;
}
}
2、有一苹果,两个人抛硬币来决定谁吃这个苹果,先抛到正面者吃。问先抛这吃到苹果的概率是多少?
这种题目一看似乎答案就是1/2,但其实认真细想并没有那么简单。给所有的抛硬币操作从1开始编号,显然先手者只可能在奇数(1,3,5,7…)次抛硬币得到苹果,而后手只可能在偶数次(2,4,6,8…)抛硬币得到苹果。设先手者得到苹果的概率为p,第1次抛硬币得到苹果的概率为1/2,在第3次(3,5,7…)以后得到苹果的概率为p/4(这是因为这种只有在第1次和第2次抛硬币都没有抛到正面(概率为1/4=1/2*1/2)的时候才有可能发生,而且此时先手者在此面临和开始相同的局面)。所以可以列出等式p=1/2+p/4,p=2/3。如题,大家懂得……
还可以这样算,1/2 + 1/8 + 1/16 +……+1/2^(奇数) = 2/3.
3、一条长度为l的线段,随机在其上选2个点,将线段分为3段,问这3个子段能组成一个三角形的概率是多少?
设随机选取的两个数为x,y,并令y>x,则把长度为1的线段截得的三段长度为x, y-x ,1-y,根据三角形两边和大于第三边以及两边之差小于第三边的定理,可以列出方程组 y>1-y; x<1-x; x+(1-y)>y-x; 即x<1/2; y>1/2; y>x+1/2;
画图可以算得概率为1/8.

4、一个面试题:快速生成10亿个不重复的18位随机数的算法(从n个数中生成m个不重复的随机数)
答案尚不明确。
5、你有两个罐子以及50个红色弹球和50个蓝色弹球,随机选出一个罐子然后从里面随机选出一个弹球,怎么给出红色弹球最大的选中机会?在你的计划里,得到红球的几率是多少?
题目意思是两个罐子里面放了50红色和50蓝色弹球,然后我任选一个罐子,从中选中一个红球的最大概率,是设计一个两个罐子里怎么放这100球的计划。一个罐子:1个红球另一个罐子:49个红球,50个篮球几率=1/2+(49/99)*(1/2)=74.7%。
6、一副扑克牌54张,现分成3等份每份18张,问大小王出现在同一份中的概率是多少?(大意如此)
解答1:
54张牌分成3等份,共有M=(C54取18)*(C36取18)*(C18取18)种分法。其中大小王在同一份的分法有N=(C3取1)*(C52取16)*(C36取18)*(C18取18)种。因此所求概率为P=N /M=17/53。
解答2:
不妨记三份为A、B、C份。大小王之一肯定在某一份中,不妨假定在A份中,概率为1/3。然后A份只有17张牌中可能含有另一张王,而B份、C份则各有18张牌可能含有另一张王,因此A份中含有另一张王的概率是17/(17+18+18)=17/53。也因此可知,A份中同时含有大小王的概率为1/3 * 17/53。题目问的是出现在同一份中的概率,因此所求概率为3*(1/3 * 17/53)=17/53。
7、A和B2人投硬币,正面A得1元,反面B得一元.起始时A有1元,B有100元. 游戏持续进行,直到其中1人破产才终止.
问:(出自投行面试题)
1.如果硬币正反概率相同,游戏的期待长度(expected duration)是几次投掷?
2.如果硬币是不公正的,正面概率为P,反面概率为Q.(P+Q=1), 那么游戏的期待长度(expectedduration)是几次投掷?
目前认为只有奇数次才可能破产。
第一问:1*1/0.5 + 3*1/0.5^3 + 5*1/0.5^5
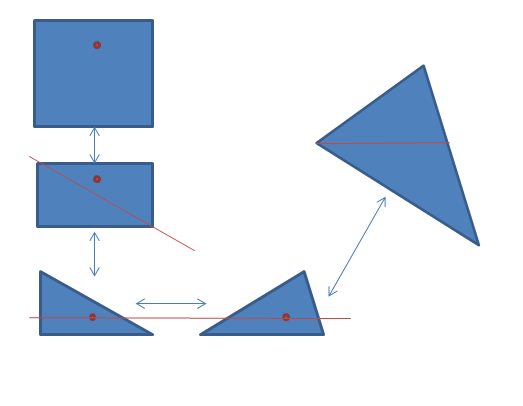
8、2D平面上有一个三角形ABC,如何从这个三角形内部随机取一个点,且使得在三角形内部任何点被选取的概率相同。
在二维坐标系中可以用坐标(x,y)来表示图形中的一个点。如下图只要能够在各个带双向箭头的图之间的点能够建立一一映射即可。如把一个长方形(如正方形)的点映射到另一个长方形的点只要把坐标做相应的放大缩小即可。如把长方形的点映射到一个直角三角形,只要将长方形右上部份的三角形的点映射到对称的左下角的三角形的点即可。而直角三角形映射到一边平行于x轴的三角形的映射只要做x轴相应的偏移即可。而任意三角形可以分割成两个其中有一边平行于x轴的三角形。说的不是很清楚,具体的映射方法可以认真思考并写出公式。
9、平均要取多少个(0,1)中的随机数才能让和超过1。答案: e 次, 其中e是自然对数的底
