一.算法
方法一:先判断矩形是否在圆内(矩形的四个顶点是否在圆内),若是则不相交,否则再判断圆心到矩形四条边的最短距离(点到线段的最短距离)是否存在小于半径的,若是则相交(认为矩形包括圆是不相交的,已经先排除了)。方法二:圆分平面为四部分,
方法二:圆分平面四部分,不相交的情况分了几种:长方形在圆形上面,长方形在圆形下面,长方形在圆形左边,长方形在圆形右边,长方形在圆形内部,圆形在长方形内部。
方法三:矩形分平面九部分,用矩形的四个边,把空间划分成为9个区域,判定圆心的位置在那个区域当中,如果在矩形的内部,则必然的相交,如果位于上下左右四个边区域当中,检测圆心到边的距离,判定是否相交,如果位于四个角点对应的区域,只要检测矩形的四个角是否在圆的内部就是了。
错误做法:
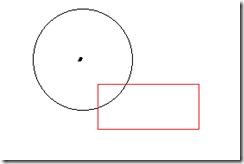
- 圆在矩形内或者矩形在圆内都不算相交,假设对角线是左下角和右上角(目测是这样,不是也没关系),若圆心不在横纵坐标范围内那么肯定不交,这种想法错误,想想矩形在圆右下角,看下图。
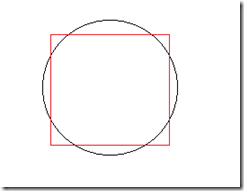
- 这样判断矩形在圆内不对,看下图
p.y+r>ymax&&p.y-r>ymin&&p.x-r>xmin&&p.x+r>xmax
不得不说做这道题收获不小……
二.算法实现
以HDU1221为例,直接去AC吧。
import java.util.Scanner; //AC了 public class W { public static void main(String[] args) { int T; double x,y; double r; Scanner sc = new Scanner(System.in); T = sc.nextInt(); while(T-->0) { x = sc.nextDouble(); y = sc.nextDouble(); //圆心 PointW p = new PointW(x,y); r = sc.nextDouble(); x = sc.nextDouble(); y = sc.nextDouble(); PointW p1 = new PointW(x,y); x = sc.nextDouble(); y = sc.nextDouble(); PointW p2 = new PointW(x,y); boolean tag = go(p,r,p1,p2); if(tag) { System.out.println("YES"); }else { System.out.println("NO"); } } } private static boolean go(PointW p, double r, PointW p1, PointW p2) { /* * 为节省内存也可以只用两个点,不要Point类,x1,y1存储xy小值,然后排列组合就得到四个点了 */ double xmin = Math.min(p1.x,p2.x); double xmax = p1.x + p2.x - xmin; double ymin = Math.min(p1.y,p2.y); double ymax = p1.y + p2.y - ymin; //矩形四点;从左下角向上、向右,再向下 PointW q1 = new PointW(xmin,ymin); PointW q2 = new PointW(xmin,ymax); PointW q3 = new PointW(xmax,ymax); PointW q4 = new PointW(xmax,ymin); boolean i = Double.compare(distance(p, q1), r)<0; boolean j = Double.compare(distance(p, q2), r)<0; boolean k = Double.compare(distance(p, q3), r)<0; boolean t = Double.compare(distance(p, q4), r)<0; //在圆内可以这样算,在圆外不能简单地把小于0改成大于0,考虑矩形贯穿圆 if(xmax<p.x-r||ymin>p.y+r||xmin>p.x+r||ymax<p.y-r) { return false; }else if(i&&j&&k&&t) { return false; }else if(p.y+r<ymax&&p.y-r>ymin&&p.x-r>xmin&&p.x+r<xmax){//在矩形内 return false; }else { return true; } } private static double distance(PointW p, PointW p1) { return Math.hypot(p.x-p1.x, p.y-p1.y); } } class PointW { double x; double y; public PointW() { this.x = 0; this.y = 0; } public PointW(double x, double y) { this.x = x; this.y = y; } }下面的wa了,路过的给瞧一瞧。
import java.util.Scanner; //wa public class HDU1221 { public static void main(String[] args) { int T; double x,y; double r; Scanner sc = new Scanner(System.in); T = sc.nextInt(); while(T-->0) { x = sc.nextDouble(); y = sc.nextDouble(); //圆心 Point p = new Point(x,y); r = sc.nextDouble(); x = sc.nextDouble(); y = sc.nextDouble(); Point p1 = new Point(x,y); x = sc.nextDouble(); y = sc.nextDouble(); Point p2 = new Point(x,y); boolean tag = go(p,r,p1,p2); if(tag) { System.out.println("YES"); }else { System.out.println("NO"); } } } private static boolean go(Point p, double r, Point p1, Point p2) { double xmin = Math.min(p1.x,p2.x); double xmax = p1.x + p2.x - xmin; double ymin = Math.min(p1.y,p2.y); //原来ymin写成了xmin double ymax = p1.y + p2.y - ymin; //矩形四点;从左下角向上、向右,再向下 Point q1 = new Point(xmin,ymin); Point q2 = new Point(xmin,ymax); Point q3 = new Point(xmax,ymax); Point q4 = new Point(xmax,ymin); boolean i = Double.compare(distance(p, q1), r)<0; boolean j = Double.compare(distance(p, q2), r)<0; boolean k = Double.compare(distance(p, q3), r)<0; boolean t = Double.compare(distance(p, q4), r)<0; if(i&&j&&k&&t) {//先排除在圆内情况,采用if else return false; }else { //等于0表示相切(tangent) i = Double.compare(pointToLine(q1,q2,p), r)<=0; j = Double.compare(pointToLine(q2,q3,p), r)<=0; k = Double.compare(pointToLine(q3,q4,p), r)<=0; t = Double.compare(pointToLine(q4,q1,p), r)<=0; if(i||j||k||t) { return true; }else { return false; } } } private static double distance(Point p, Point p1) { return Math.hypot(p.x-p1.x, p.y-p1.y); } //点到线段的最短距离,x0,y0是圆心 private static double pointToLine(Point p1,Point p2, Point p) { double ans = 0; double a, b, c; a = distance(p1, p2); b = distance(p1, p); c = distance(p2, p); if (c+b==a) {//点在线段上 ans = 0; return ans; } if (a<=1e-8) {//不是线段,是一个点 ans = b; return ans; } if (c*c >= a*a + b*b) { //组成直角三角形或钝角三角形,p1为直角或钝角 ans = b; return ans; } if (b * b >= a * a + c * c) {// 组成直角三角形或钝角三角形,p2为直角或钝角 ans = c; return ans; } // 组成锐角三角形,则求三角形的高 double p0 = (a + b + c) / 2;// 半周长 double s = Math.sqrt(p0 * (p0 - a) * (p0 - b) * (p0 - c));// 海伦公式求面积 ans = 2*s / a;// 返回点到线的距离(利用三角形面积公式求高) return ans; } } class Point { double x; double y; public Point() { this.x = 0; this.y = 0; } public Point(double x, double y) { this.x = x; this.y = y; } }