需要代码联系作者,不做义务咨询。
一.算法实现
基于p-stable分布,并以‘哈希技术分类’中的分层法为使用方法,就产生了E2LSH算法。
E2LSH中的哈希函数定义如下:
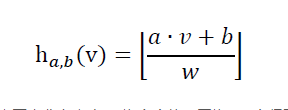
其中,v为d维原始数据,a为随机变量,由正态分布产生; w为宽度值,因为a∙v+b得到的是一个实数,如果不加以处理,那么起不到桶的效果,w是E2LSH中最重要的参数,调得过大,数据就被划分到一个桶中去了,过小就起不到局部敏感的效果。b使用均匀分布随机产生,均匀分布的范围在[0,w]。
但是这样,得到的结果是(N1,N2,…,Nk),其中N1,N2,…,Nk在整数域而不是只有0,1两个值,这样的k元组就代表一个桶。但将k元组直接当做桶标号存入哈希表,占用内存且不便于查找,为了方便存储,设计者又将其分层,使用数组+链表的方式。
对每个形式为k元组的桶标号,使用如下h1函数和h2函数计算得到两个值,其中h1的结果是数组中的位置,数组的大小也相当于哈希表的大小,h2的结果值作为k元组的代表,链接到对应数组的h1位置上的链表中。在下面的公式中,r’为[0,prime-1]中依据均匀分布随机产生。
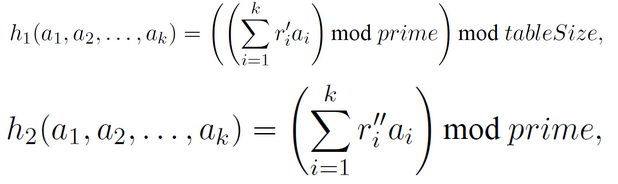
经过如上操作后,查询步骤如下。
对于查询点query,
使用k个哈希函数计算桶标号的k元组;
对k元组计算h1和h2值,
获取哈希表的h1位置的链表,
在链表中查找h2值,
获取h2值位置上存储的样本
Query与上述样本计算精确的相似度,并排序
按照顺序返回结果。
E2LSH方法存在两方面的不足[8]:首先是典型的基于概率模型生成索引编码的结果并不稳定。虽然编码位数增加,但是查询准确率的提高确十分缓慢;其次是需要大量的存储空间,不适合于大规模数据的索引。E2LSH方法的目标是保证查询结果的准确率和查全率,并不关注索引结构需要的存储空间的大小。E2LSH使用多个索引空间以及多次哈希表查询,生成的索引文件的大小是原始数据大小的数十倍甚至数百倍。
部分参考文献:http://dataunion.org/12912.html
二.遗留问题
2.1 hash过后不是还需要由hash吗找到原来的点么,怎么实现?
2.2 球p稳定分布例子
2.3 k元组存入多个哈希表?那查找的结果是什么?每个表中的结果的并?
三.问题扩展
E2LSH可以说是分层法基于p-stable distribution的应用。另一种当然是转换成hashcode,则定义哈希函数如下:

其中,a和v都是d维向量,a由正态分布产生。同上,选择k个上述的哈希函数,得到一个k位的hamming码,按照”哈希技术分类”中描述的技术即可使用该算法。
找我要代码可以,但是请不要白嫖行吗? 各种问来问去,愿意出5块钱,或者100块还要考虑几天。
1.让我实现一篇论文(论文还得我自己看),聊了半天,就愿意出10块钱,你特码在逗我;
2.让我改进一篇论文,然后给他讲讲论文和代码,再想想创新点实现创新代码,并写出主要步骤画出图,愿意出几百而已;
3.让我完全定题目和创新点并写小论文,然后说完全做好给钱;我原来真这样,给南京某几个学校的两个个学生做完,
讲好的价钱,视频验完,结果不要了。草,我当时真是想给你曝光,当然最后没有曝光。基本诚信都没,我相信你,你却这个样子。
4.脾气臭的屌丝,我耐心引导你理清思路(自己要是思路清晰地话就剩下写代码的事情而已),结果动不动发火。行,你多给点钱也行啊,
结果没过半小时直接把我删了;
5.还有若干博士,让我先给个创新点,各种保证一定给钱,我想着博士嘛,没事。结果我给他讲完,他各种佩服,结果直接把我拉黑了(北京某985的)..
上过硕士的都知道idea是最重要的..没idea啥都没
KP7L6G16E0.png)