聚类评价指标

 一、引言

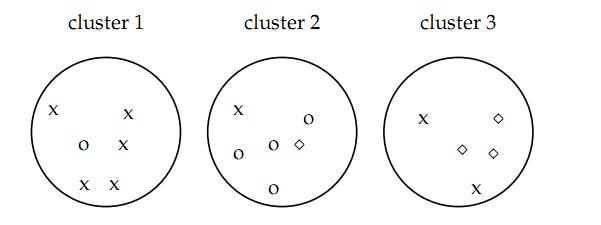
　　如图认为x代表一类文档，o代表一类文档，方框代表一类文档，完美的聚类显然是应该把各种不同的图形放入一类，事实上我们很难找到完美的聚类方法，各种方法在实际中难免有偏差，所以我们才需要对聚类算法进行评价看我们采用的方法是不是好的算法。

二、评价准则

　　2.1 purity

　　1）purity方法是极为简单的一种聚类评价方法，只需计算正确聚类的文档数占总文档数的比例：

　　其中Ω = {ω1,ω2, . . . ,ωK}是聚类的集合ωK表示第k个聚类的集合。C = {c1, c2, . . . , cJ}是文档集合，cJ表示第J个文档。N表示文档总数。

　　如上图的purity = ( 3+ 4 + 5) / 17 = 0.71

　　其中第一类正确的有5个，第二个4个，第三个3个，总文档数17。

　　purity方法的优势是方便计算，值在0～1之间，完全错误的聚类方法值为0，完全正确的方法值为1。同时，purity方法的缺点也很明显它无法对退化的聚类方法给出正确的评价，设想如果聚类算法把每篇文档单独聚成一类，那么算法认为所有文档都被正确分类，那么purity值为1！而这显然不是想要的结果。

　　2）另一种表述:使用上述Entropy中的定义，我们将聚类 i 的purity定义为。整个聚类划分的purity为，其中K是聚类（cluster）的数目，m是整个聚类划分所涉及到的成员个数。

　　2.2 RI

　　实际上这是一种用排列组合原理来对聚类进行评价的手段，公式如下：

　　其中TP是指被聚在一类的两个文档被正确分类了，TN是只不应该被聚在一类的两个文档被正确分开了，FP只不应该放在一类的文档被错误的放在了一类，FN只不应该分开的文档被错误的分开了。对上图

TP＋FP ＝ C(2,6) + C(2,6) + C(2,5) = 15 + 15 + 10 = 40，其中C(n,m)是指在m中任选n个的组合数。

TP = C(2,5) + C(2,4) + C(2,3) + C(2,2) = 20

FP = 40 - 20 = 20

　　相似的方法可以计算出TN = 72 FN = 24

　　所以RI ＝ ( 20 + 72) / ( 20 + 20 + 72 +24) = 0.68

　　2.3 F-measure

　　评价方法三：F值

　　这是基于上述RI方法衍生出的一个方法，

　　RI方法有个特点就是把准确率和召回率看得同等重要，事实上有时候我们可能需要某一特性更多一点，这时候就适合F值方法

　　2.4 Entropy

　　对于一个聚类i，首先计算。指的是聚类 i 中的成员（member）属于类（class）j 的概率，。其中是在聚类 i 中所有成员的个数，是聚类 i 中的成员属于类 j 的个数。每个聚类的entropy可以表示为，其中L是类（class）的个数。整个聚类划分的entropy为，其中K是聚类（cluster）的数目，m是整个聚类划分所涉及到的成员个数。

 三、实例分析

　　下表是对取自洛杉矶时报的3204篇文章进行的k-means划分的结果，共分为6个cluster。这些文章取自娱乐、金融等六个类别。理想情况下每个cluster只含有某一特定类别的文章。其中，cluster 3 与体育类别吻合的比较好，所以其entropy很低，purity很高。

五、参考文献

　　http://blog.csdn.net/luoleicn/article/details/5350378

　　http://blog.csdn.net/vernice/article/details/46467449