数据结构----prim算法 最小生成树

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

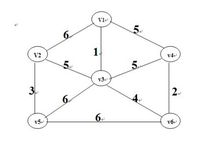
 选择一个点作为起点      判断连接每个节点的度   选择最小的     每进一个节点 标记已经来过  如果一个节点所连接的节点都走过了 那么就退一步 继续寻找连接边   选择最小的  

#include <stdio.h>
#define MAXN 7

int martix[MAXN][MAXN] = {
	{0,1,3,0,0,0,5},
	{1,0,0,4,0,0,6},
	{3,0,0,0,4,0,3},
	{0,4,0,0,0,7,2},
	{0,0,4,0,0,1,5},
	{0,0,0,7,1,0,2},
	{5,6,3,2,5,2,0}
};




void find(int * min,int x,int * ex){
	//printf("%d 处理中..",x);
	printf("%d->",x);
	int pos;
	int mini=99999;
	int j,i;
	int flag=0;
	while(1){
		//printf("%d 处理中3....",x);
		for(j=0;j<MAXN;j++){
			if(martix[x][j]!=0){
				if(ex[j]==1){
					flag=1;
				}else{
					flag=0;
					//printf("x:%d j:%d没有访问值为%d
",x,j,martix[x][j]);
					break;
				}
			}
		}
		if(flag){
			break;
		}
		else{
			mini=99999;
			for(j=0;j<MAXN;j++){
			//printf("%d",j);
				if(martix[x][j]!=0&&martix[x][j]<mini&&ex[j]==0){
					mini = martix[x][j];
					pos = j;
				}
			}
			ex[pos] = 1;
			//printf("设置%d为1
",pos);
			min[pos] = martix[x][pos];
			find(min,pos,ex);
		}
	}
	//printf("%d完成了
",x);
}




int main(){
	int i,k,j,m,pos_x,pos_y;
	int min_d[MAXN];
	int ex[MAXN];
	for(i=0;i<MAXN;i++){
		min_d[i]=99999;
	}
	for(j=0;j<MAXN;j++){
		ex[j]=0;
	}
	ex[0] = 1;
	find(min_d,0,ex);
	for(i=0;i<MAXN;i++){
		printf("%d
",min_d[i]);
	}
}