Python 多项式拟合（一元回归）

一元一阶线性拟合：

假设存在一条线性函数尽量能满足所有的点：y=ax+b .对所有点的的公式为：

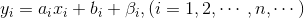
  残差值β = 实际值y - 估计值y，β 应尽量小，当 β = 0 时，则完全符合一元线性方程：y=ax+b

 

  通过最小二乘法计算残差和最小：

 

  根据微积分，当 Q 对 a、b 的一阶偏导数为了0时，Q 达到最小。

 

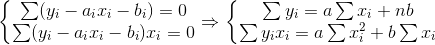
  解方程组，求 a、b 的值：

 

 

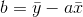
 示例：

 

如客户的贷款金额及还款金额情况，设 x 为贷款金额，预测Y为还款金额。（也可以当做收入与消费的情况）

 通过公式计算相应的值：

解得：

a = 655131.86/2194469.14 = 0.2985
b = 172.64-a*598.24 = -5.93464

 即得回归方程为： Ÿ = 0.2985*x - 5.93464

回归方程验证：

Y 的第 i 个观察值与样本值的离差 ，点与回归线在 Y 轴上的距离。总离差分解为两部分为：

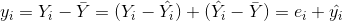
实际观测值与回归拟合值之差，为回归直线不能解释的部分：

样本回归拟合值与观测值的平均值之差，为回归直线可解释的部分：

其中，设总体平方和为：

即得 回归平方和为：

 

残差平方和为：

 

即： TSS=ESS+RSS

 样本中，TSS不变， 如果实际观测点离样本回归线越近，则ESS在TSS中占的比重越大.

拟合优度：

R² 为（样本）可决系数/判定系数（coefficient of determination)，取值范围：[0，1]。R²越接近1，说明实际观测点离样本线越近，拟合优度越高。一般地要求R²≥0.7。

计算结果;

 R²  =  1 - 72279.48 / 267861.07 =  0.73016 

 python 方法实现：

#-*- coding: utf-8 -*-
# python 3.5.0

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
from sklearn.linear_model import LinearRegression 

df = pd.read_table('D:/Python35/mypy/test.txt')
x = np.asarray(df[['x']])
y = np.asarray(df[['y']])
reg = LinearRegression().fit(x, y)
print("一元回归方程为:  Y = %.5fX + (%.5f)" % (reg.coef_[0][0], reg.intercept_[0]))
print("R平方为: %s" % reg.score(x, y))

plt.scatter(x, y,  color='black')
plt.plot(x, reg.predict(x), color='red', linewidth=1)
plt.show()

 

一元多阶线性拟合（多项式拟合）：

 假设存在一个函数，只有一个自变量，即只有一个特征属性，满足多项式函数如下：

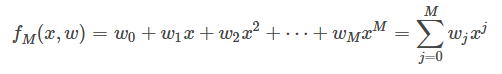
损失函数：损失函数越小，就代表模型拟合的越好。

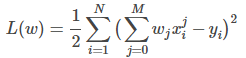
通过对损失函数偏导为0时，得到最终解方程的函数：

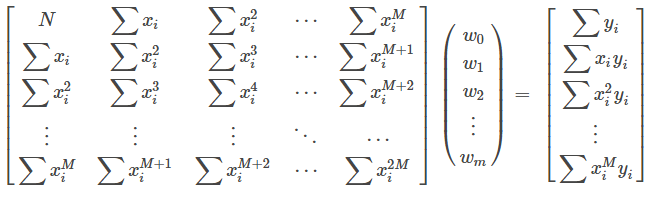
公式推导参考：

https://www.zhihu.com/question/23483726

http://blog.csdn.net/xiaolewennofollow/article/details/46757657

https://wenku.baidu.com/view/f20f3e0da8956bec0875e343.html?from=search

python numpy.polyfit 实现：（此处 x 只有一个特征，属于一元多阶函数）

 假设因变量 y 刚好符合该公式。

import numpy as np
import matplotlib.pyplot as plt

x = np.array([-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10])
y = np.array(2*(x**4) + x**2 + 9*x + 2) #假设因变量y刚好符合该公式
#y = np.array([300,500,0,-10,0,20,200,300,1000,800,4000,5000,10000,9000,22000])

# coef 为系数，poly_fit 拟合函数
coef1 = np.polyfit(x,y, 1)
poly_fit1 = np.poly1d(coef1)
plt.plot(x, poly_fit1(x), 'g',label="一阶拟合")
print(poly_fit1)

coef2 = np.polyfit(x,y, 2)
poly_fit2 = np.poly1d(coef2)
plt.plot(x, poly_fit2(x), 'b',label="二阶拟合")
print(poly_fit2)

coef3 = np.polyfit(x,y, 3)
poly_fit3 = np.poly1d(coef3)
plt.plot(x, poly_fit3(x), 'y',label="三阶拟合")
print(poly_fit3)

coef4 = np.polyfit(x,y, 4)
poly_fit4 = np.poly1d(coef4)
plt.plot(x, poly_fit4(x), 'k',label="四阶拟合")
print(poly_fit4)

coef5 = np.polyfit(x,y, 5)
poly_fit5 = np.poly1d(coef5)
plt.plot(x, poly_fit5(x), 'r:',label="五阶拟合")
print(poly_fit5)

plt.scatter(x, y, color='black')
plt.legend(loc=2)
plt.show()

其中5个函数拟合如下：

可以看到，只要最高阶为4阶以上，如 四阶拟合 和 五阶拟合，拟合函数近乎完全是符合原函数 y = 2*(x**4) + x**2 + 9*x + 2，拟合是最好的，几乎没有产生震荡，没有过拟合。

当将因变量 y 更换如下：

x = np.array([-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10])
y = np.array([300,500,0,-10,0,20,200,300,1000,800,4000,5000,10000,9000,22000])

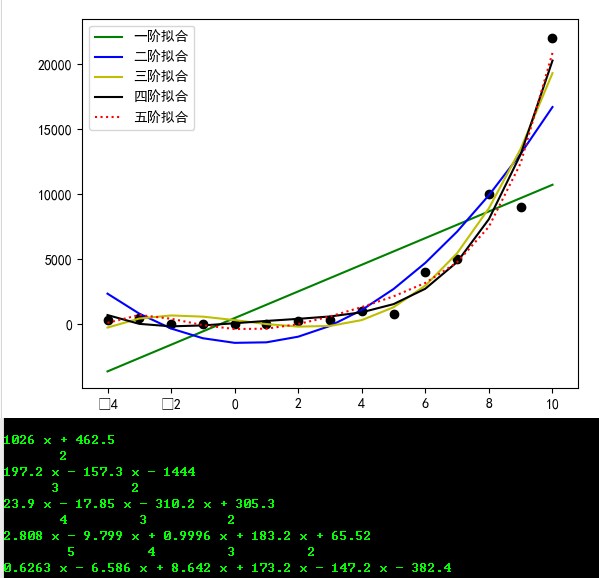
结果发现，四阶及以上拟合程度较高。当设置阶数越高，震荡越明显，也就过度拟合了。怎样确定拟合函数或者最高阶呢？ 参考：Python 确定多项式拟合/回归的阶数