环形链表进阶版【手绘漫画】面试必考之双指针（LeetCode 142）

文章目录

• 图解算法与数据结构
• 1、前言
• 2、实例
• 3、正文
• 4、代码

图解算法与数据结构

1、前言

今天开始的是双指针！

下面一起来看看吧！！！

让我们从一个经典问题开始：

给定一个链表，判断链表中是否有环。

你可能已经使用 哈希表 提出了解决方案。但是，使用 双指针 技巧有一个更有效的解决方案。

想象一下，有两个速度不同的跑步者。如果他们在直路上行驶，快跑者将首先到达目的地。但是，如果它们在圆形跑道上跑步，那么快跑者如果继续跑步就会追上慢跑者。

这正是我们在链表中使用两个速度不同的指针时会遇到的情况：

1. 如果没有环，快指针将停在链表的末尾。
2. 如果有环，快指针最终将与慢指针相遇。

所以剩下的问题是：

这两个指针的适当速度应该是多少？

一个安全的选择是每次移动慢指针一步，而移动快指针两步。每一次迭代，快速指针将额外移动一步。如果环的长度为 M，经过 M 次迭代后，快指针肯定会多绕环一周，并赶上慢指针。

为了让你更懂，下面来看一个题吧！

2、实例

LeetCode 142，一个求证链表中有没有环的题。

3、正文

一起来看一下：

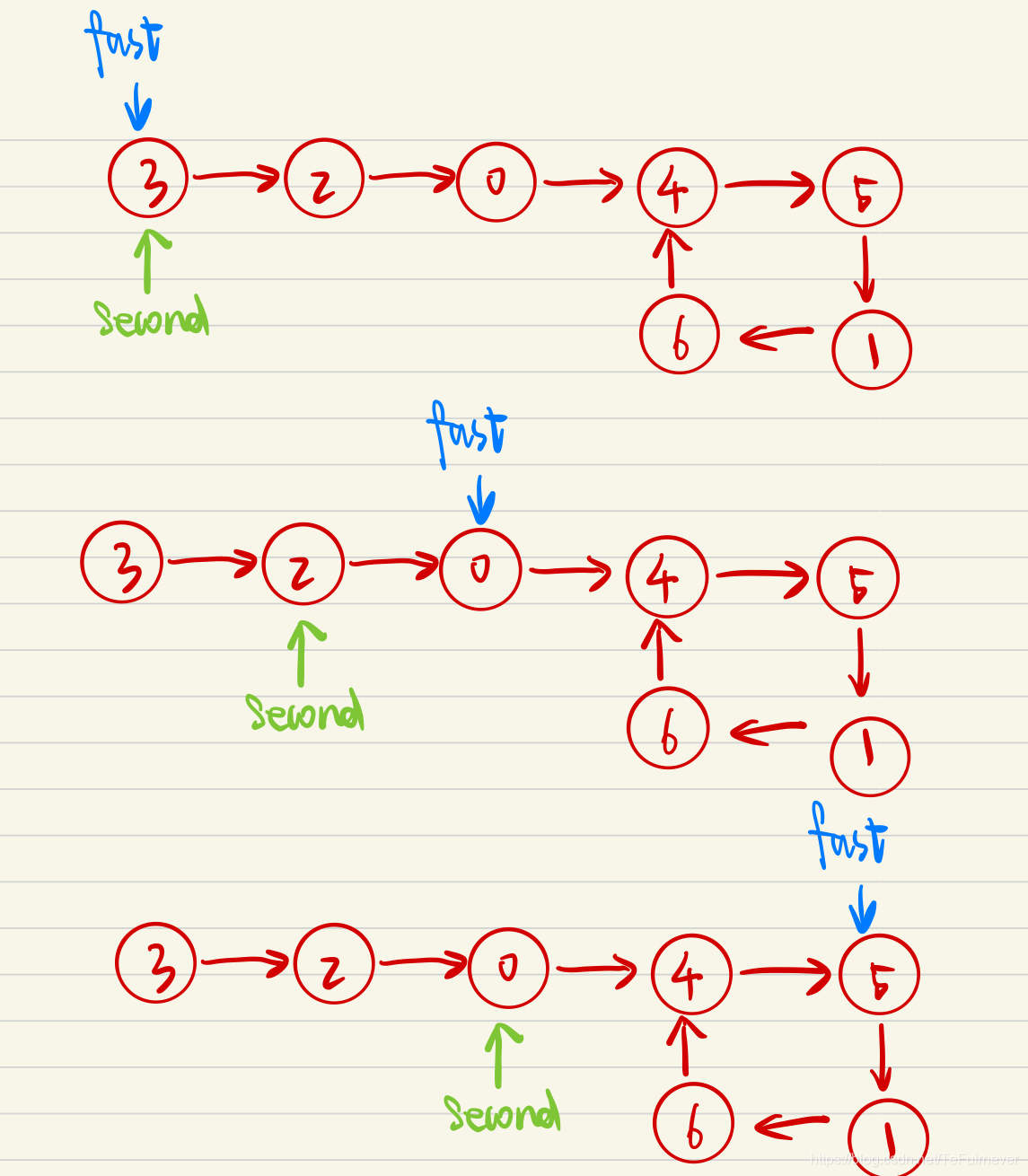
1. 双指针初始化：

   1. 设双指针 fast，slow 指向链表头部 head；
   2. fast 每轮走 1 步；
   3. slow 每轮走 1 步；

2. 两种情况：

   1. 第一种情况：不出意外，fast 每轮再多走 1 步（这才是名副其实的快指针~）；
      
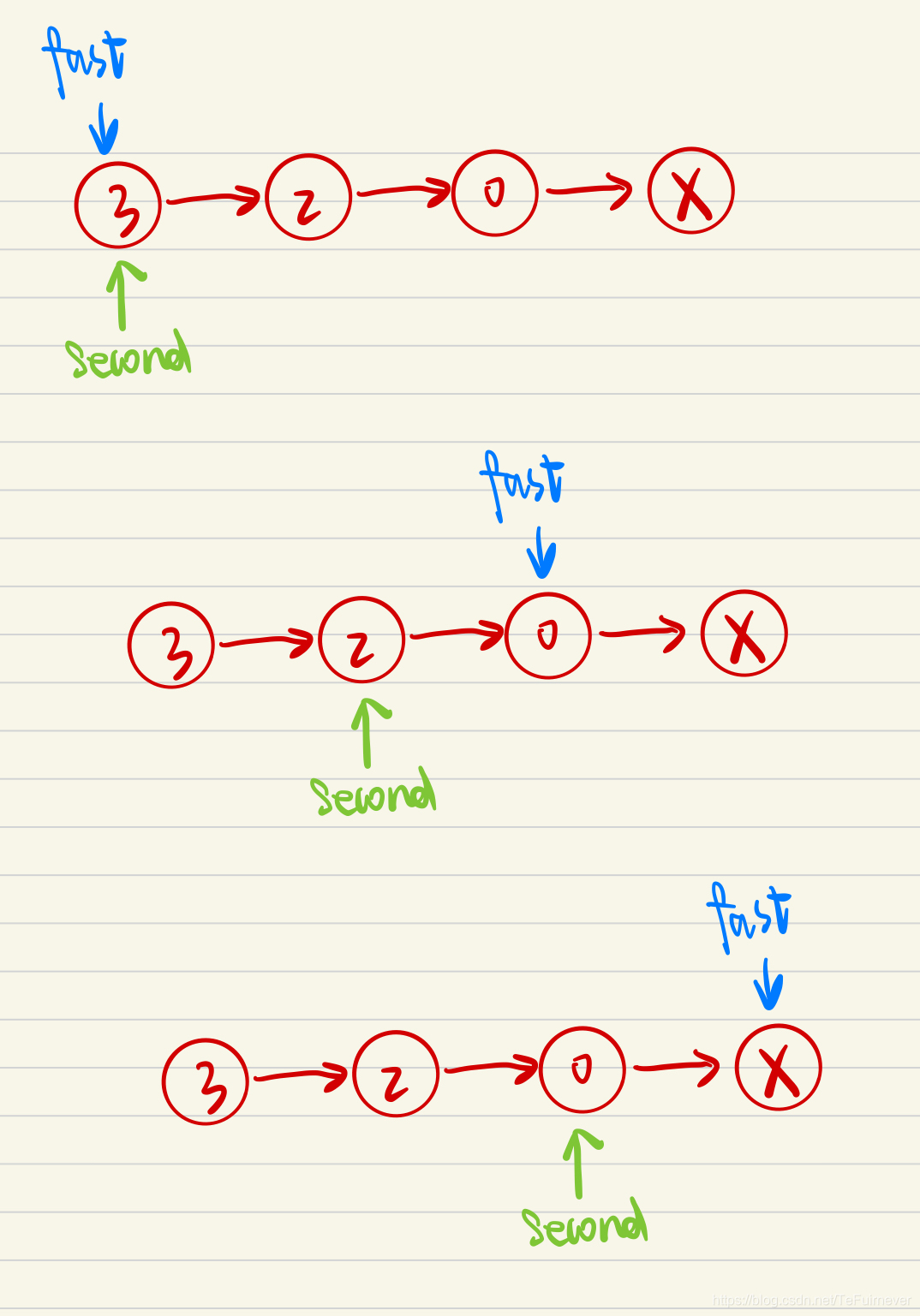
   2. 第二种情况：fast 走到链表末端，下一节点为空，说明链表无环，直接 break，返回 NULL（如果存在环，两个指针必然会相遇，追击问题，fast 速度是 slow 的二倍~）；
      

3. 双指针第一次相遇（当 fast == slow 时）：

   1. 设链表共有 a+b 个节点，其中 链表头到环的入口 有 a 个节点（不算环入口节点），环 有 b 个节点，若两指针分别走了 f，s 步（fast，slow 的英文缩写）；
   2. 路程等于速度乘以时间，fast 的速度是 slow 的 2 倍，所以 fast 走的步数是 slow 的 2 倍，即 f = 2*s ①；
   3. 双指针最后都是在环内绕圈直到重合，所以 fast 比 slow 多走了 n 个环的长度，即 f = s + n*b ②；
   4. 以上两式 ① ② 相减得：f = 2n*b，s = n*b，即 fast 和 slow 分别走了 2n，n 个 环。
      

4. 双指针第二次相遇（当 fast == slow 时）：

   1. slow 指针不动，fast 重新指向链表头节点（f = 0，s = n*b）；
   2. slow 和 fast 同时每轮向前走 1 步；
   3. 当 fast 走 f = a 步时，slow 走 s = a+nb 步，此时 两指针重合，并同时指向环入口（b 是环的长度！整数倍 b 就是环入口）。
      

5. 返回 fast 指针指向的节点（slow 也行，因为终止条件是 fast == slow）。

---

这个位置有个非常灵性的操作，即：

分析分析：

问：如何才能恰好在环入口节点相遇呢？

答：如果走过的路程满足 a+n*b，n 可以是任意自然数值（0，1，2…），先走 a 步到环入口节点，之后无论绕多少圈环（n*b 步）都会再次回到入口节点，即相遇了~~~~而现在这个时间点，slow 走过的步数是 nb，只要想办法再走 a 步停下来，就可以到环的入口，同时 fast 也要走 a 步，这样两者就相遇了！所以依然是双指针法，fast 重新初始化为链表头 head，这样走 a 步就到了环入口，而 slow 也走 a 步，变成了 a+n*b，到达了环入口节点。

妙啊！！！

4、代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        auto fast=head,slow=head;
        while(fast){
            fast=fast->next;
            slow=slow->next;
            if(fast) fast=fast->next;
            else break;

            if(fast==slow){
                fast=head;
                while(fast!=slow){
                    fast=fast->next;
                    slow=slow->next;
                }
                return fast;
            } 
        }
        return NULL;
    }
};

如果有幸帮到你，请帮我点个【赞】，给个【关注】！如果能顺带【评论】给个鼓励，我将不胜感激。

如果想要更多的资源，欢迎关注 @我是管小亮，文字强迫症MAX~