【2020-MOOC-浙江大学-陈越、何钦铭-数据结构】树（第三周的笔记和编程作业）

文章目录

• 〇、前言
• 一、树的定义
• 二、树的基本术语
• 三、二叉树
• 四、性质
• 五、二叉树基本操作
• 六、二叉树遍历
• 1、先序遍历
• 2、中序遍历
• 3、后序遍历
• 4、层序遍历
• 七、树的同构
• 八、课后题
• 1、03-树1 树的同构 (25分)
• 2、03-树2 List Leaves (25分)
• 3、03-树3 Tree Traversals Again (25分)
• 总结

〇、前言

这两周开始跟着【MOOC-浙江大学-陈越、何钦铭-数据结构】进行数据结构与算法的学习，特此记录复习一下，虽然记不住，但是一直记一直记一直记，成为复读机就好了。

一、树的定义

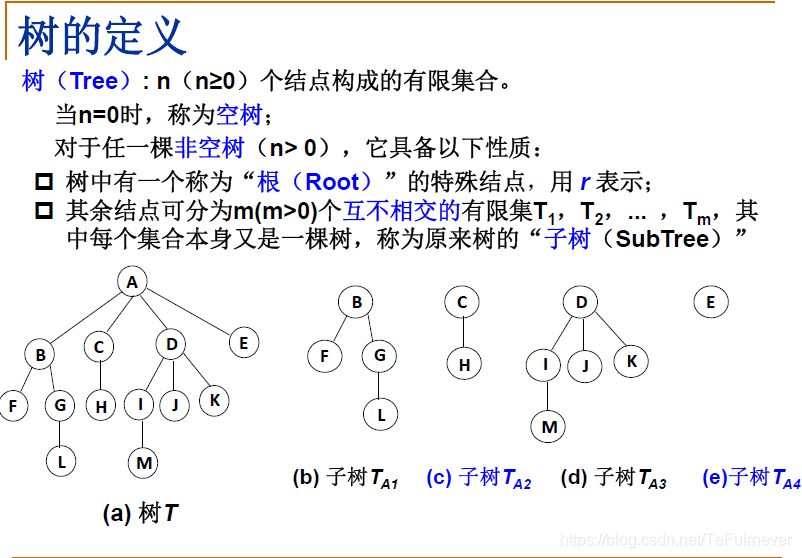
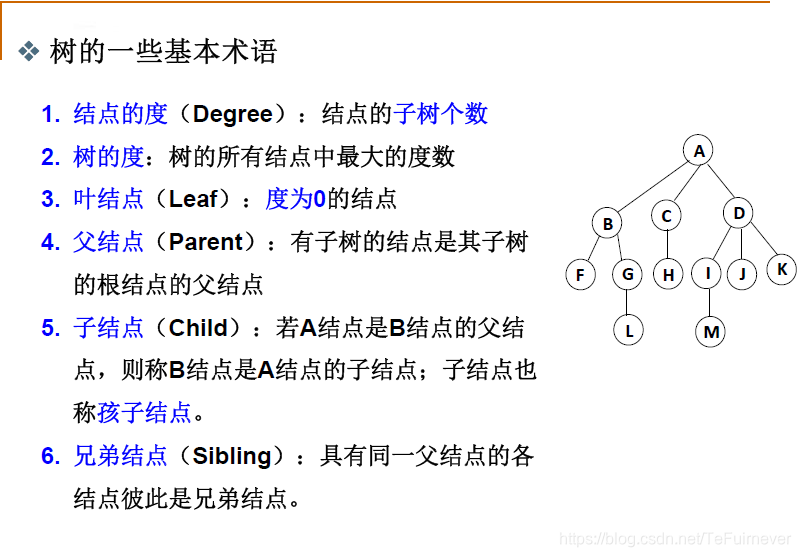
二、树的基本术语

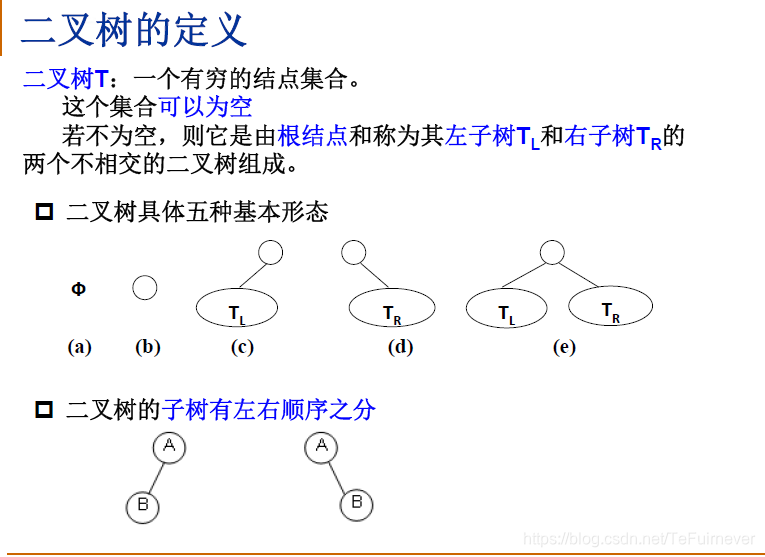
三、二叉树

四、性质

五、二叉树基本操作

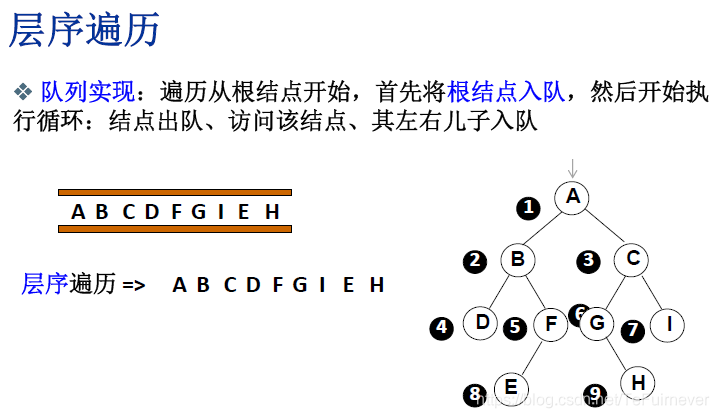
六、二叉树遍历

1、先序遍历

2、中序遍历

3、后序遍历

4、层序遍历

七、树的同构

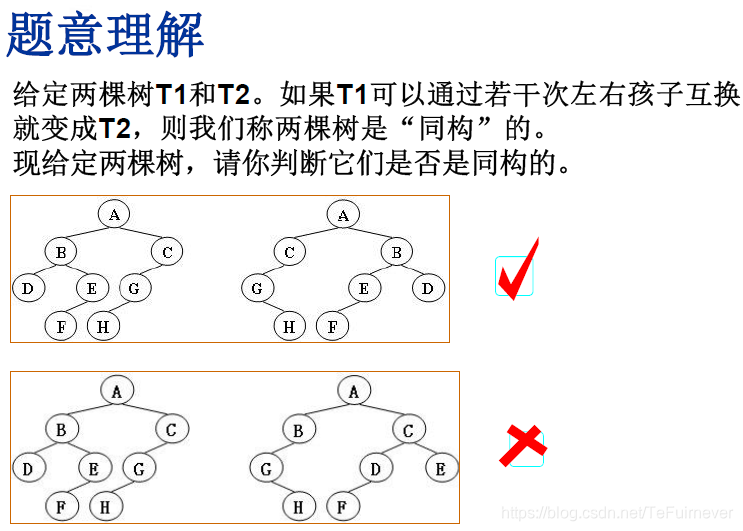
实现在后面的第一题！

八、课后题

---

1、03-树1 树的同构 (25分)

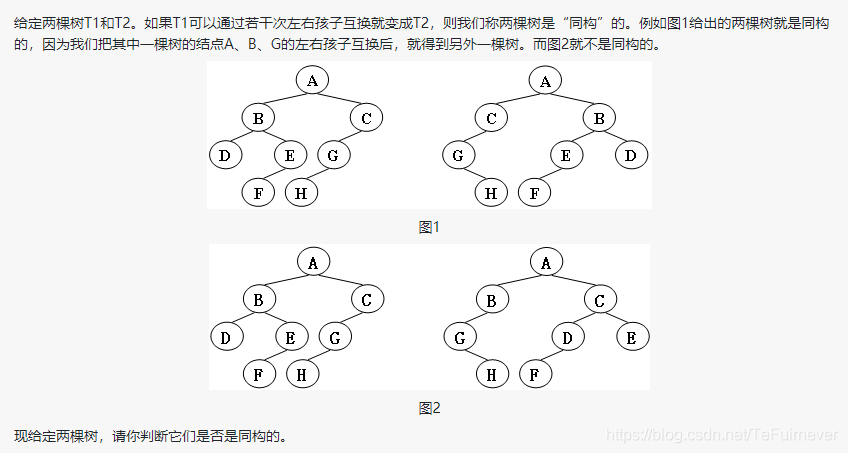
输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

---

#include <stdio.h>
#define MaxTree 10
#define ElementType char
#define Tree int
#define Null -1

struct TreeNode{
	ElementType Element;
	Tree Left;
	Tree Right;
}T1[MaxTree],T2[MaxTree];

Tree BuildTree(struct TreeNode T[]){
	int N,i,check[MaxTree],Root=Null;
	ElementType cl,cr;
	scanf("%d
",&N);
	if(N){
		for(i=0;i<N;i++)
			check[i]=0;
		for(i=0;i<N;i++){
			scanf("%c %c %c
",&T[i].Element,&cl,&cr);
			if(cl!='-'){
				T[i].Left=cl-'0';
				check[T[i].Left]=1;
			}
			else{
				T[i].Left=Null;
			}
			if(cr!='-'){
				T[i].Right=cr-'0';
				check[T[i].Right]=1;
			}
			else{
				T[i].Right=Null;
			}
		}
		for(i=0;i<N;i++){
			if(!check[i]){
				Root=i;
				break;
			}
		}
	}
	return Root;
}

int Isomorphic(Tree R1,Tree R2){
    //两树为空树，则为同构
	if((R1==Null)&&(R2==Null))
		return 1;
    //一个树为空，另一个不为空，则不同构
	if(((R1==Null)&&(R2!=Null))||((R1!=Null)&&(R2==Null)))
		return 0;
    //两树根结点存在但数据不同，则不同构
	if(T1[R1].Element!=T2[R2].Element)
		return 0;
    //两树左子树均为空树，则判断两树右子树是否同构
	if((T1[R1].Left==Null)&&(T2[R2].Left==Null))
		return Isomorphic(T1[R1].Right,T2[R2].Right);
	//两树左子树不为空，且两树左子树数据相等，则判断两树左子树和右子树是否同时同构
	if((T1[T1[R1].Left].Element==T2[T2[R2].Left].Element)&&(T1[R1].Left!=Null)&&(T2[R2].Left!=Null))
		return (Isomorphic(T1[R1].Left,T2[R2].Left)&&Isomorphic(T1[R1].Right,T2[R2].Right));
	//否则交换判断子树是否同构
    else
		return (Isomorphic(T1[R1].Left,T2[R2].Right)&&Isomorphic(T1[R1].Right,T2[R2].Left));
	
}

int main(){
	Tree R1,R2;
	R1=BuildTree(T1);
	R2=BuildTree(T2);
	if(Isomorphic(R1,R2))
		printf("Yes
");
	else
		printf("No
");
}

---

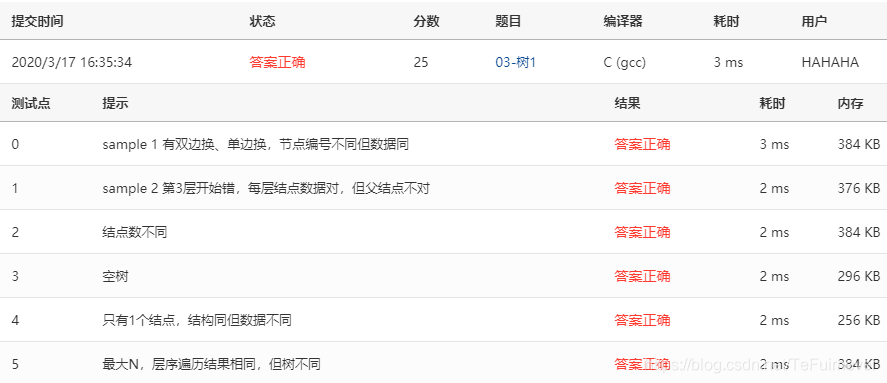
2、03-树2 List Leaves (25分)

Sample Input:

8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6

Sample Output:

4 1 5

---

#include <stdio.h>
#include <stdlib.h>

#define MaxTree 10
#define Tree int
#define Null -1

struct TreeNode {
    Tree Left;
    Tree Right;
} T1[MaxTree];

#define QueueSize 100
typedef int Position;
typedef int ElementType;
struct QNode {
    ElementType *Data;     /* 存储元素的数组 */
    Position Front, Rear;  /* 队列的头、尾指针 */
    int MaxSize;           /* 队列最大容量 */
};
typedef struct QNode *Queue;
 
Queue CreateQueue( int MaxSize )
{
    Queue Q = (Queue)malloc(sizeof(struct QNode));
    Q->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
    Q->Front = Q->Rear = 0;
    Q->MaxSize = MaxSize;
    return Q;
}
 
int IsFull( Queue Q )
{
    return ((Q->Rear+1)%Q->MaxSize == Q->Front);
}
 
int AddQ( Queue Q, ElementType X )
{
    if ( IsFull(Q) ) {
        printf("队列满");
        return;
    }
    else {
        Q->Rear = (Q->Rear+1)%Q->MaxSize;
        Q->Data[Q->Rear] = X;
        return;
    }
}
 
int IsEmpty( Queue Q )
{
    return (Q->Front == Q->Rear);
}
 
ElementType DeleteQ( Queue Q )
{
    if ( IsEmpty(Q) ) { 
        printf("队列空");
        return Null;
    }
    else  {
        Q->Front =(Q->Front+1)%Q->MaxSize;
        return  Q->Data[Q->Front];
    }
}

Tree BuildTree(struct TreeNode T[])
{
    char cl, cr;
    int N, i, check[MaxTree];
    Tree Root = Null;
    scanf("%d
", &N);
    if(N) {
        for(i=0;i<N;i++)
            check[i] = 0;
        for(i=0;i<N;i++) {
            scanf("%c %c
", &cl, &cr);
            if(cl!='-') {
                T1[i].Left = cl - '0';
                check[T1[i].Left] = 1;
            } else
                T1[i].Left = Null; 

            if(cr!='-') {
                T1[i].Right = cr - '0';
                check[T1[i].Right] = 1;
            } else
                T1[i].Right = Null;
        }
        for(i=0;i<N;i++)
            if(check[i] != 1) break;
        Root = i;
    }
    return Root;
}

void PrintLeaves(Tree R)    //层序遍历
{
    Queue Q;
    Tree cur;
    int count = 0;
    if(R==Null) return;
    Q=CreateQueue(QueueSize);
    AddQ(Q, R);
    while(!IsEmpty(Q)) {
        cur = DeleteQ(Q);
        if((T1[cur].Left == Null) && (T1[cur].Right == Null)) {
            if(!count) {
                printf("%d", cur);
                count++;
            } 
			else{
            	printf(" %d", cur);
            	continue;
			}
        }
        if(T1[cur].Left!=Null) AddQ(Q, T1[cur].Left);
        if(T1[cur].Right!=Null) AddQ(Q, T1[cur].Right);
    }
}

int main()
{
    Tree R;
    R = BuildTree(T1);
    PrintLeaves(R);
    return 0;
}

---

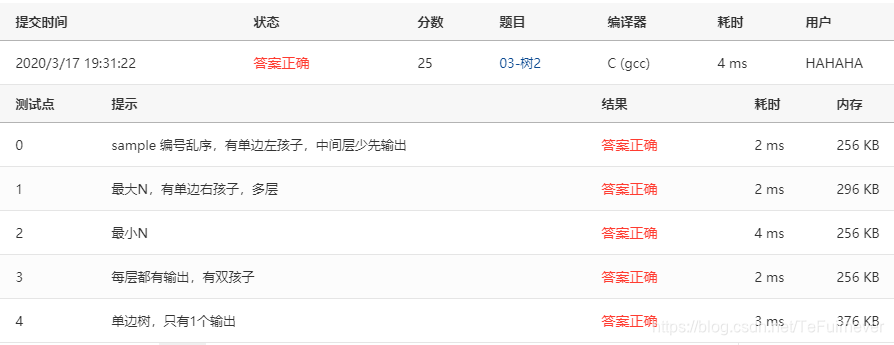
3、03-树3 Tree Traversals Again (25分)

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

Sample Output:

3 4 2 6 5 1

---

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <string.h>

int count = 0;

typedef struct TreeNode *BinTree;
struct TreeNode {
    int Data;
    BinTree Left;
    BinTree Right;
};

typedef struct SNode *Stack;
struct SNode {
    BinTree Data;
    Stack Next;
};

BinTree CreateBinTree(int data)
{
    BinTree head;
    head = (BinTree)malloc(sizeof(struct TreeNode));
    head->Data = data;
    head->Left = NULL;
    head->Right = NULL;
    return head;
}

int IsEmptyBinTree(BinTree BST)
{
    return (BST == NULL);
}

void InsertLeftLeafe(BinTree BST, int leftData)
{
    BinTree left;
    left = (BinTree)malloc(sizeof(struct TreeNode));
    left->Data = leftData;
    left->Left = NULL;
    left->Right = NULL;
    BST->Left =  left;
}

void InsertRightLeafe(BinTree BST, int rightData)
{
    BinTree right;
    right = (BinTree)malloc(sizeof(struct TreeNode));
    right->Data = rightData;
    right->Left = NULL;
    right->Right = NULL;
    BST->Right =  right;
}

Stack CreateStack()
{
    Stack S = (Stack)malloc(sizeof(struct SNode));
    S->Data = NULL;
    S->Next = NULL;
    return S;
}

int IsEmptyStack(Stack S)
{
    return (S->Next == NULL);
}

void StackPush(Stack S, BinTree pos)
{
    Stack TmpCell = (Stack)malloc(sizeof(struct SNode));
    TmpCell->Data = pos;
    TmpCell->Next = S->Next;
    S->Next = TmpCell;
}

BinTree StackPop(Stack S)
{
    Stack FirstCell;
    BinTree pos;
    if(S->Next == NULL) {
        printf("Stack Empty");
        return NULL;
    } 
	else {
        FirstCell = S->Next;
        S->Next = FirstCell->Next;
        pos = FirstCell->Data;
        free(FirstCell);
        return pos;
    }
}

void PrintStack(Stack S)
{
    Stack head = S;
    while(head) {
        printf("%p ", head->Next);
        head = head->Next;
    }
    printf("
");
}

BinTree Read()
{
    int N, data, count=0;
    char str[10];
    Stack S = CreateStack();
    BinTree head;
    BinTree BT = CreateBinTree(0);
    head = BT;
    scanf("%d
", &N);
    scanf("Push %d
", &BT->Data);
    StackPush(S, BT);
    count++;
    if(N) {
        while(!IsEmptyStack(S)||count<N) {      //是否堆栈为空，输入足够的结点
            scanf("%s", str);
            if(strcmp("Push", str) == 0) {      //区分Push和Pop
                scanf("%d", &data);
                if(BT->Left == NULL) {
                    InsertLeftLeafe(BT, data);
                    BT = BT->Left;
                    StackPush(S, BT);
                    count++;
                } 
				else if(BT->Right==NULL) {
                    InsertRightLeafe(BT, data);
                    BT = BT->Right;
                    StackPush(S, BT);
                    count++;
                } 
				else {
                    printf("can't go here
");
                }
            }
			else {
                BT = StackPop(S);
            }
        }
        return head;
    }
    return NULL;
}

void PostOrderTraversal(BinTree BT){

	if(BT){
		PostOrderTraversal(BT->Left); 
		PostOrderTraversal(BT->Right); 
		if(!count) {
            printf("%d", BT->Data);
            count++;
        } 
		else {
            printf(" %d", BT->Data);
        }
	}
}

int main()
{
    int N;
    BinTree BT;
    BT = Read();
    PostOrderTraversal(BT);

    return 0;
}

总结

简单总结下这周的学习内容，二叉树应该是数据结构的一大难点了，日常自闭，写了博客是为了能找着平板写一写代码，只能背一背了！！！

如果想要更多的资源，欢迎关注 @我是管小亮，文字强迫症MAX~

回复【数据结构】即可获取我为你准备的大礼

想看更多文（段）章（子），欢迎关注微信公众号「程序员管小亮」~