《机器学习》周志华西瓜书习题参考答案：第1章

【机器学习】《机器学习》周志华西瓜书 笔记/习题答案 总目录

• https://blog.csdn.net/TeFuirnever/article/details/96178919

——————————————————————————————————————————————————————

• 【机器学习】《机器学习》周志华西瓜书读书笔记：第1章 - 绪论

习题

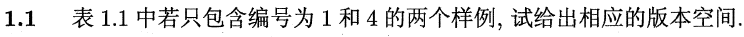
此时训练集如下：

编号	色泽	根蒂	敲声	好瓜
1	青绿	蜷缩	浊响	是
4	乌黑	稍蜷	沉闷	否

由于好瓜的3个属性值与坏瓜都不同。所以能与训练集一致的假设就有很多可能了，从最具体的入手，往上逐层抽象可得：

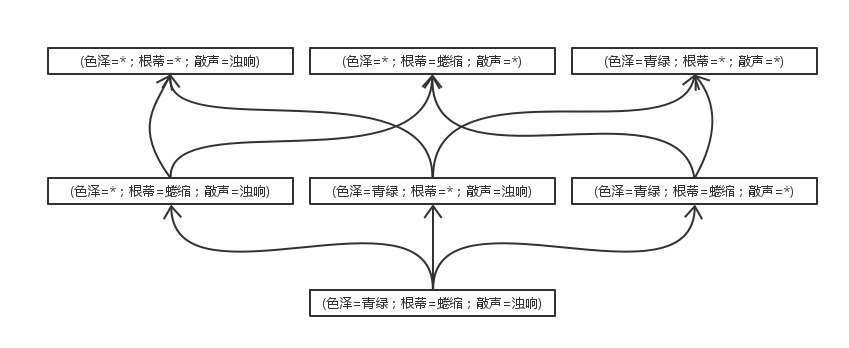
首先要理解题意，“使用最多包含 $k$ 个合取式的析合范式来表达表1.1西瓜分类问题的假设空间” 。

这句话表达的意思是每个假设可以由最少1个、最多k个合取范式的析取来表示。

表1.1：

编号	色泽	根蒂	敲声	好瓜
1	青绿	蜷缩	浊响	是
2	乌黑	蜷缩	浊响	是
3	青绿	硬挺	清脆	否
4	乌黑	稍蜷	沉闷	否

这里色泽有2种取值，根蒂有3种取值，敲声有3种取值。因为每个属性还可以用通配符表示取任何值都行，所以实际上这三个属性分别有3，4，4种选择。因此，在只考虑单个合取式的情况下，有 $3 imes 4 imes 4 = 48$ 种假设（因为训练集中有存在正例，所以 $varnothing$ 假设不需考虑）。

现在我们考虑题目的条件，这实际上是一个组合问题。我们可以从48个基本假设中任意去1个到k个组合为新的假设：

• 使用1个合取式：$inom{48}{1} = 48$ 种假设；

• 使用2个合取式：$inom{48}{2} = frac{48*47}{2*1} = 1128$ 种假设；

• …

• 使用k个合取式：$inom{48}{k} = frac{48*47*...*(48-k+1)}{k!}$ 种假设；

若不考虑冗余的问题，就把以上求得的各情形下的假设个数进行求和就得到问题的答案了。

如果考虑冗余的问题，这个博客有说明，但是我现在第一遍看书，就先留个坑。

• 归纳偏好是在无法断定哪一个假设更好的情况下使用的。既然问题是存在噪声，那么如果能知道噪声的分布（例如高斯噪声），就可以将这些性能相同的假设对应的误差减去由噪声引起的部分，此时再使用奥卡姆剃刀原则或者多释原则来进行假设选择就好了。更常见的做法是引入 正则化（regularization） 项，在建立模型时避免拟合噪声。
• 若认为两个数据的属性越相近，则更倾向于将他们分为同一类。若相同属性出现了两种不同的分类，则认为它属于与他最临近几个数据的属性。也可以考虑同时去掉所有具有相同属性而不同分类的数据，留下的数据就是没误差的数据，但是可能会丢失部分信息。

回顾NFL的证明可以发现，关键是要证明，在考虑所有可能的目标函数（对应所有可能的问题，或者说样本空间的所有分布情况）时，模型的性能变得与学习算法无关。也即证明 $sum_f ell(h(x), f(x))$ 最终可以化简为与常数形式。

当我们考虑所有可能的$f$，并且$f$均匀分布时，任务就失去了优化目标，无论使用哪一种算法，所得模型的平均性能会变得相同。或者可以考虑信号检测中的代价函数推导，只要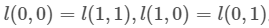，就可以直接轻松证明。

如果想看更严谨的推导可以看Wolpert, D.H., Macready, W.G当初写的论文"No Free Lunch Theorems for Optimization"。

这题比较开放，最常见的，消息推送，比如某宝；网站相关度排行，通过点击量，网页内容进行综合分析；图片搜索或者视频搜索。

参考文章

• 机器学习（周志华）课后习题
• https://blog.csdn.net/snoopy_yuan/article/category/6788615