浅谈KMP字符串匹配算法

Ⅰ、预备知识

(KMP)，全称(Knuth-Morris-Pratt)算法，可以实现高效搜索一个模式串P(长为m)在文本串S(长为n）中出现的位置，其核心是处理(next)数组，预处理模式串失配后将匹配的位置，从而实现高效搜索
普通的模式串搜索，是暴力一位一位枚举(S[i])与(P[j])是否相等，不相等则往后移一位，重新匹配
代码大概长这样：

inline void check(char *p,char *s){
    int i=1,j=1,lst=1;
    while(1){
        if(j==m+1)
            return lst;
        if(s[i]==p[j])
            i++,j++;
        else
            j=1,i=++lst;
    }
}

很明显，这种写法做了许多无用功，一些显然无法匹配的段也要(O(m))去搜索。最坏情况下，这种写法可以被卡成(O(n imes m))
于是，(kmp)算法诞生了
(kmp)的核心思想为不一位一位暴力匹配，而是通过Next数组大大减少匹配数量
Next数组表示什么呢？
设(s_{ildots j})表示字符串(s)的第(i)位到第(j)位，i表示文本串已经处理了多少点，j表示模式串已经匹配了多少点
Next数组表示当(s1[i+1]!=s2[j+1])时，即模式串与文本串下一位失配时，j指针要去往的位置(s1表示文本串,s2表示模式串)

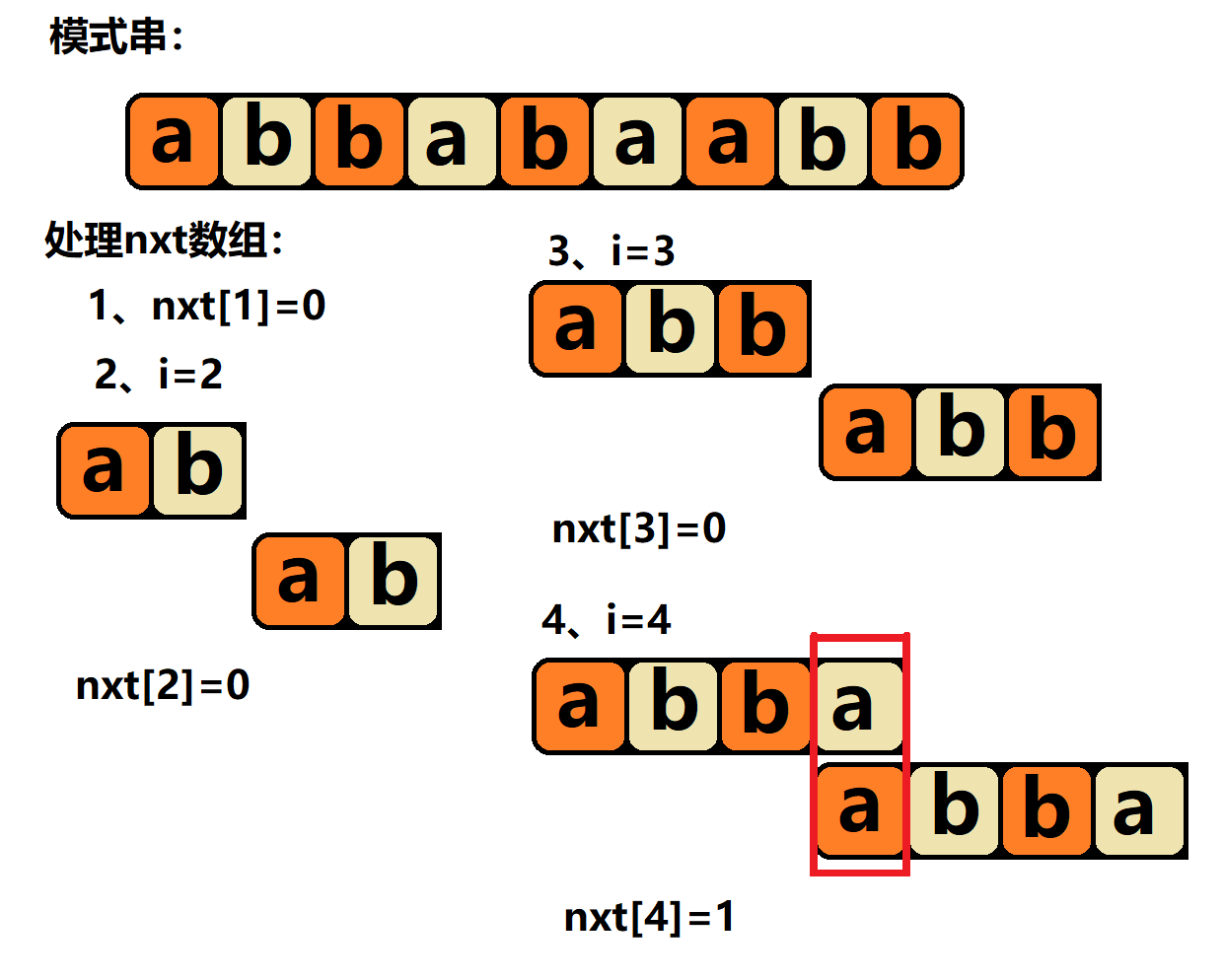
如图，当i=4,j=4时，如果模式串的下一位与文本串的下一位不匹配，则j就转移到Next[j]，即1，使得j再次与i匹配
显然，处理nxt数组可以通过求最长严格前缀与后缀公共串的长度得到
以下代码:

inline void get_Next(){
	int j=0;
	F(i,1,l2){//l2为模式串的长度
		while(j&&s2[j+1]!=s2[i+1])//s2为模式串，如果没有跳到头就继续匹配
			j=Next[j];//失配就往前跳
		if(s2[j+1]==s2[i+1])//如果下一位相同
			j++;//模式串+1
		Next[i+1]=j;//处理Next数组
	}
}

接下来就是模式串匹配，思路和求Next数组差不多，匹配则往后一位，失配则跳Next数组，代码如下：

inline void kmp(){
	int j=0;
	F(i,0,l1-1){
		while(j&&s2[j+1]!=s1[i+1])//失配
			j=Next[j];
		if(s2[j+1]==s1[i+1])
			j++;
		if(j==l2){//匹配成功
			printf("%d
",i-j+2);//此处为(i+1)-j+1
			j=Next[j];//继续找所有的匹配串
		}
	}
}