数据结构的分类
数据机构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成
常用的数据结构有:数组,栈,链表,队列,树,图,堆,散列表等,如图所示
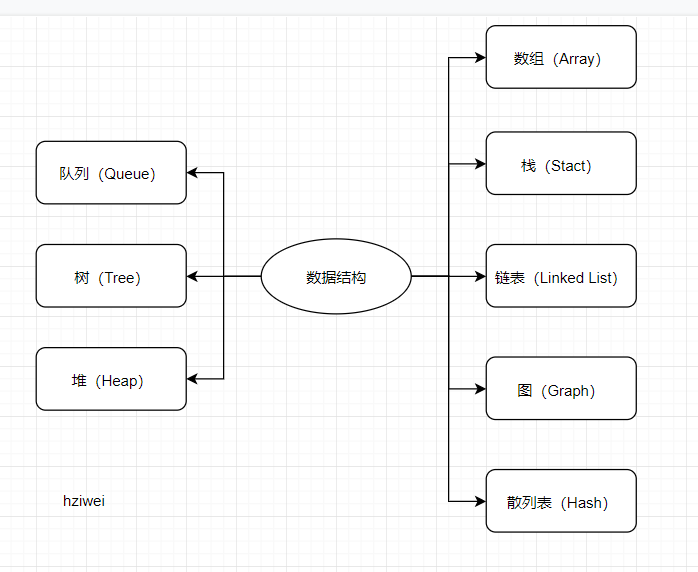
不同的数据结构有着不同的数据存储的方式
1、数组
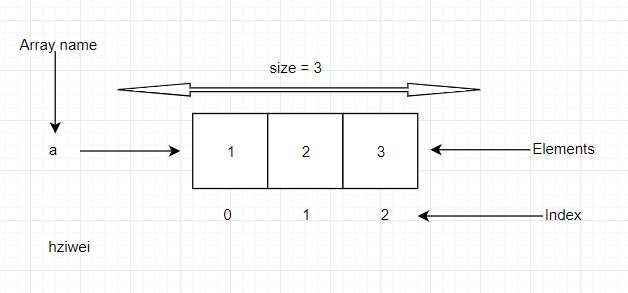
数组是可以在内存中连续存储多个元素的结构,在内存中的分配也是连续的,数组中的元素通过数组的下标开始访问,数组的下标是从0开始的
-
数组运算
(1、遍历:遍历所有元素并进行打印
(2、插入:将一个或多个元素插入数组
(3、删除:从数组中删除元素
(4、搜索:在数组中搜索元素,可以按照元素的值或者索引搜索元素
(5、更新:更新指定索引的值 -
数组的优点
(1、按照索引插叙元素速度快
(2、按照索引遍历数组方便 -
数组的缺点
(1、数组只能存储一种类型的数据
(2、添加、删除元素的操作慢,因为要移动其它元素 -
应用场景
(1、是用于构建其他数据结构的基础,如数组列表、堆、哈希表、向量和矩阵
(2、用于不同的排序算法,如插入排序、快速排序、冒泡排序和合并排序
(3、用于频繁查询,对存储空间要求不大,很少增加和删除元素的情况
2、栈
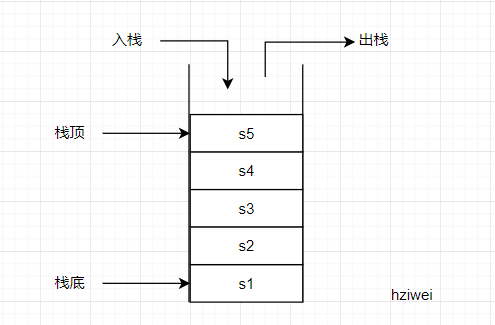
栈是一种特殊的线性表,仅能在线性表的一端操作,栈顶允许操作,栈底不允许操作。 栈的特点是:先进后出,或者说是后进先出,从栈顶放入元素的操作叫入栈,取出元素叫出栈。
-
堆栈操作
(1、push推送:在栈顶部插入一个元素
(2、pop弹出:取出最上面的元素并返回 -
特性
栈的结构就像是货车,最早放进入去的东西最晚拿出来 -
栈的应用
(1、用于表达式评估,如:用于解析和评估数学表达式的调车场算法
(2、用于在递归编程中实现函数调用
3、队列
队列和栈一样,也是一种线性表,不同的是,队列可以在一端添加元素,在另一端取出元素,也就是:先进先出,放入元素的操作成为入队,取出元素为出队
-
队列操作
(1、进队:将元素插入到队列的末尾
(2、出队:从队列的开头删除元素 -
特性
类似现实世界中的队列 -
队列的应用
(1、用于管理多线程中的线程
4、链表
链表是物理存储单元上非连续的、非顺序的存储结构,数据元素的逻辑顺序是通过链表的指针地址实现,每个元素包含两个结点,一个是存储元素的数据域 (内存空间),另一个是指向下一个结点地址的指针域。根据指针的指向,链表能形成不同的结构,例如单链表,双向链表,循环链表等。
-
链表术语
(1、链表中的元素称为节点。
(2、每个节点都包含一个密钥和一个指向其后继节点(称为next)的指针。
(3、名为head的属性指向链接列表的第一个元素。
(4、链表的最后一个元素称为尾。 -
链表类型
(1、单链列表—只能沿正向遍历项目。
(2、双链表-可以在前进和后退方向上遍历项目。节点由一个称为上一个的附加指针组成,指向上一个节点。
(3、循环链接列表—链接列表,其中头的上一个指针指向尾部,尾号的下一个指针指向头。

-
链表操作
(1、搜索:通过简单的线性搜索在给定的链表中找到键为k的第一个元素,并返回指向该元素的指针。
(2、插入:在链接列表中插入一个密钥。插入可以通过3种不同的方式完成;在列表的开头插入,在列表的末尾插入,然后在列表的中间插入。
(3、删除:从给定的链表中删除元素x。您不能单步删除节点。删除可以通过3种不同方式完成;从列表的开头删除,从列表的末尾删除,然后从列表的中间删除。 -
链表的优点:
(1、链表是很常用的一种数据结构,不需要初始化容量,可以任意加减元素;
(2、添加或者删除元素时只需要改变前后两个元素结点的指针域指向地址即可,所以添加,删除很快; -
链表的缺点:
(1、因为含有大量的指针域,占用空间较大;
(2、查找元素需要遍历链表来查找,非常耗时。 -
链表的应用
数据量较小,需要频繁增加,删除操作的场景
5、树
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做 “树” 是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
-
特点
(1、每个节点有零个或多个子节点;
(2、没有父节点的节点称为根节点;
(3、每一个非根节点有且只有一个父节点;
(4、除了根节点外,每个子节点可以分为多个不相交的子树; -
树的应用
(1、二叉树:用于实现表达式解析器和表达式求解器。
(2、二进制搜索树:用于许多不断输入和输出数据的搜索应用程序中。
(3、堆:由JVM(Java虚拟机)用来存储Java对象。
(4、Trap:用于无线网络。 -
扩展
二叉树有很多扩展的数据结构,包括平衡二叉树、红黑树、B+树等,这些数据结构二叉树的基础上衍生了很多的功能,在实际应用中广泛用到,例如mysql的数据库索引结构用的就是B+树,还有HashMap的底层源码中用到了红黑树。
6、散列表
散列表,也叫哈希表,是根据关键码和值 (key和value) 直接进行访问的数据结构,通过key和value来映射到集合中的一个位置,这样就可以很快找到集合中的对应元素。
-
特性
这里的对应关系 f 成为散列函数,又称为哈希 (hash函数),而散列表就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里,这种存储空间可以充分利用数组的查找优势来查找元素,所以查找的速度很快 -
散列表的应用
哈希表的应用场景很多,当然也有很多问题要考虑,比如哈希冲突的问题,如果处理的不好会浪费大量的时间,导致应用崩溃。
7、堆
堆是一种比较特殊的数据结构,可以被看做一棵树的数组对象
-
性质
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。 -
类型
(1、最小堆:父项的密钥小于或等于子项的密钥。这称为min-heap属性。根将包含堆的最小值。
(2、最大堆数:父项的密钥大于或等于子项的密钥。这称为max-heap属性。根将包含堆的最大值。 -
堆的应用
(1、用于实现优先级队列,因为可以根据堆属性对优先级值进行排序。
(2、可以在O(log n)时间内使用堆来实现队列功能。
(3、用于查找给定数组中k个最小(或最大)的值。
(4、因为堆有序的特点,一般用来做数组中的排序,称为堆排序。
8、图
一个图由一组有限的顶点或节点以及一组连接这些顶点的边组成。
图的顺序是图中的顶点数。图的大小是图中的边数。
如果两个节点通过同一边彼此连接,则称它们为相邻节点。
-
分类
(1、有向图:
如果图形G的所有边缘都具有指示什么是起始顶点和什么是终止顶点的方向,则称该图形为有向图。
我们说(u,v)从顶点u入射或离开顶点u,然后入射到或进入顶点v。
自环:从顶点到自身的边。
(2、无向图:
如果图G的所有边缘均无方向,则称其为无向图。它可以在两个顶点之间以两种方式传播。如果顶点未连接到图中的任何其他节点,则称该顶点为孤立的。 -
图的应用
(1、用于表示社交媒体网络。每个用户都是一个顶点,并且在用户连接时会创建一条边。
(2、用于表示搜索引擎的网页和链接。互联网上的网页通过超链接相互链接。每页是一个顶点,两页之间的超链接是一条边。用于Google中的页面排名。
(3、用于表示GPS中的位置和路线。位置是顶点,连接位置的路线是边。用于计算两个位置之间的最短路径。