A-Sorce:
题意:给一个字符串(只含有‘O’和'X'),如果包含连续'O'那么从第一个O开始分数从1开始按照公差为1的等差数列递增如“OOO”那么分数为1+2+3,如果遇到'X'那么下个'O'又从1开始,如“OOXOO”,分数为1+2+1+2。
分析:水题,直接上代码。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 int t; 5 string str; 6 scanf("%d",&t); 7 while (t--){ 8 cin>>str; 9 int ans = 0,cnt = 1; 10 for (int i = 0; i < str.size(); i++){ 11 if (str[i] == 'O') ans += cnt++; 12 else cnt = 1; 13 } 14 printf("%d ",ans); 15 } 16 return 0; 17 }
B-Tetrahedron:
题意:给一个四面体,顶点为A,B,C,D,刚开始位于D点,输入一个n,问从D出发向其他顶点移动n步又回到D总共有多少种方案,结果取余1e9+7。
分析:如果说第n步回到了D点,那么第n-1步一定不在D点,那么所有第n-1到达不在D点的点的方案数之和就是第n步到达d点的方案数,由此可以想到用dp求解。
设D编号为0,A编号为1,B编号为2,C编号为3,dp[i][j]为第i步到达j号节点的方案数。那么显然有转移方程:dp[i][j] = sum(dp[i-1][k])其中k != j。
最后只需要求出 dp[n][0]表示第n步到D节点的方案数就好了。

1 #include<cstdio> 2 using namespace std; 3 const int maxn = 1e7+5; 4 const int mod = 1e9+7; 5 int dp[maxn][4]; 6 int n; 7 int main(){ 8 scanf("%d",&n); 9 dp[1][0] = 0; 10 dp[1][1] = dp[1][2] = dp[1][3] = 1; 11 for (int i = 1; i <= n; i++){ 12 for (int j = 0; j < 4; j++){ 13 for (int k = 0; k < 4; k++){ 14 if (j == k) continue; 15 dp[i][j] += dp[i-1][k]; 16 dp[i][j] %= mod; 17 } 18 } 19 } 20 printf("%d",dp[n][0]); 21 return 0; 22 }
C - Permute Digits:
题意:给两个数a,b(0<=a,b<=1e18),输出a中数排序后小于等于b的最大数,输出不含前导0,题目保证有解。
分析:思路是一位一位操作使得每次操作都得到当前位最优的情况下的可行解(也就是a<b)[参考题解的操作非常巧妙,先对a排序,然后用l和r记录位置,每次操作交换a[l]和a[r]交换完毕后判断a和b的大小关系然后对当前操作a的位(l)之后的位再升序排序,每次一旦a<b可行便终止,这样可以保证得到的解是最优的]。有一点积累到了a、b用字符串读入,a<b和把字符串a、b转化成对于整数的a<b是等价的。
对于之前模拟的思路:如果b长度大于a a排序大到小输出 根据题意,如果a长度大于b 那么输出必然含前导0或者无解 但题目说不含0且有解 所以a不可能大于b a等于b的话 从b的第一位开始找 在a中找与b相等的数,如果找到了就放入答案数组末尾,b后移一位 直到找不到为止,因为题目保证有解所以不可能a中所有数都比b的第一位大 如果找不到相等的了因为一定有解一定能在a中找到一个小于b当前位的最大的数,把它放入答案数组 剩下a中的数排序后从大到小依次放到答案数组 最后输出答案数组。如果当前循环找不到用dfs回溯找下一个可行解。这个思路居然是错误的,但目前还未找到错误的原因。。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 string a,b,tmp; 5 cin>>a>>b; 6 int lena = a.length(),lenb = b.length(); 7 sort(a.begin(),a.end()); 8 if (lena<lenb){ 9 for (int i = lena-1; i>= 0; i--){ 10 printf("%c",a[i]); 11 } 12 puts(""); 13 } 14 else{ 15 int l,r; 16 for (l = 0; l < lena; l++){ 17 r = lena-1; 18 tmp = a; 19 while (l<r){ 20 swap(a[l],a[r--]); 21 sort(a.begin()+l+1,a.end()); 22 if (a > b) a = tmp; 23 else break; 24 } 25 } 26 cout<<a<<endl; 27 } 28 return 0; 29 }
D - Ehab and a 2-operation task:
题意:给一个数n,然后给出n个数(a1,a2……an),现可以对这n个数进行两种操作:1.进行i x操作,代表a1到ai个数都加上x、2.进行i x操作,代表a1到ai个数都modx。使得数列(a1,a2……an)为递增数列 题目要求操作数小于等于n+1。0<=ai<=1e5,n<=2000,0<=x<=1e6。输出一个数字包含总操作数量,随后是每个操作的内容 第一个数代表操作编号 第二个数i 第三个数x。
分析:关键在于n+1个操作,因为ai<=1e5 只需要先对每个数加上1e5(共1次操作),然后i从1到n递增 每个a[1]到a[i] mod a[i] - i (共n次操作) 便可得到一个(1,2,3,……n)的递增数列。总操作数恰好为n+1。

#include<bits/stdc++.h> using namespace std; int arr[2005]; int main(){ int n; scanf("%d",&n); for (int i = 1; i <= n; i++){ scanf("%d",&arr[i]); arr[i] += 1e5; } printf("%d ",n+1); printf("1 %d 100000 ",n); for (int i = 1; i<= n; i++){ printf("2 %d %d ",i,arr[i]-i); } return 0; }
E - System Administrator:
题意: 第一行给一个n代表n组数据。然后给出n组数据,每组数据包含三个数 t x y 代表当前计算机属于t组(只有2组a和b 题目说t=1代表是a,t!=1都代表是b),x代表成功数,y代表丢失数,x+y总数为10。如果说一个组中的成功数大于等于总数的一半,那么输出LIVE否则输出DEAD,实际上只要输出两个组就好了。(实实在在的大水题,只是英文劝退)
分析:水题,直接上代码。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int all[2] = {0},now[2] = {0}; 4 int main(){ 5 int n,t,x,y; 6 scanf("%d",&n); 7 while (n--){ 8 scanf("%d%d%d",&t,&x,&y); 9 if (t==1){ 10 all[0] += 10; 11 now[0] += x; 12 } 13 else{ 14 all[1] += 10; 15 now[1] += x; 16 } 17 } 18 if (now[0] >= all[0]/2) printf("LIVE "); else printf("DEAD "); 19 if (now[1] >= all[1]/2) printf("LIVE "); else printf("DEAD "); 20 return 0; 21 }
F-Squares:
题意:开始看了半天没看懂,后来mqf分析后发现是水题,就是先输入一个n再输入一个k,然后输入n个数字(a1,a2……an),找出一个点包含于k个 (0,0)点与(ai,ai)点组成的正方形 之内。
分析:水题,直接上代码。

#include<bits/stdc++.h> using namespace std; int arr[55]; int main(){ int n,k; scanf("%d %d",&n,&k); for (int i = 0; i < n; i++) scanf("%d",&arr[i]); if (k>n) printf("-1"); else{ sort(arr,arr+n); printf("%d %d",arr[n-k],arr[n-k]); } return 0; }
G - Jumping Jack:
题意:初始位于0,给一个坐标n,每次可以向左或者向右跳,跳的距离为(1,2,3,4,5……)也就是下一次跳的距离比这次多1,第一次跳的距离是1,问跳到n最少要几次。
分析:乍一看很像搜索,但范围太广,MLE。后经mqf分析应该是数学思维题。赛后想了挺久没想出来,于是看了一下题解。。。
首先给的n可以是负数,但可以根据对称性把所有情况都化为n为正数的情况,也就是如果n为负数就把n变为-n。
此时我们从0点向右走,要在最短的步数内到达n,当然是要朝着n的方向走。我们一直朝着n走,可能会很幸运刚好走到n,但通常情况下我们不会那么凑巧刚好走到n,而是会走到某处,
当我们再跳一次时就会超过n,此时需要借助向左跳来处理这种情况。
我们先来分析一下向左跳一次会得到什么结果:
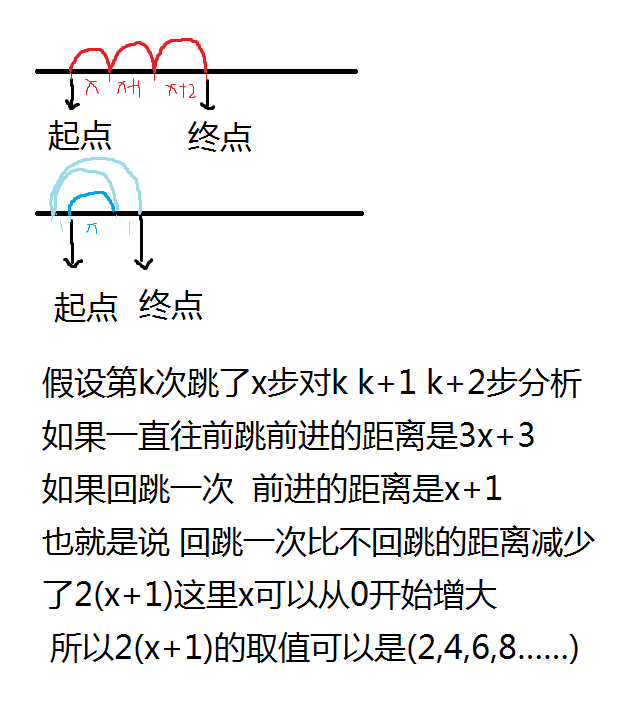
那么也就是说,向左跳一次再向右跳会相对于一直向右跳减少2的倍数的距离,那么如果我们跳到某处时再跳一步就超过n,而超过n的距离刚好是个偶数
那么我们完全可以通过在之前的某处回跳一次在接着往右跳使得我们恰好能够跳到n,下面的图片分析:
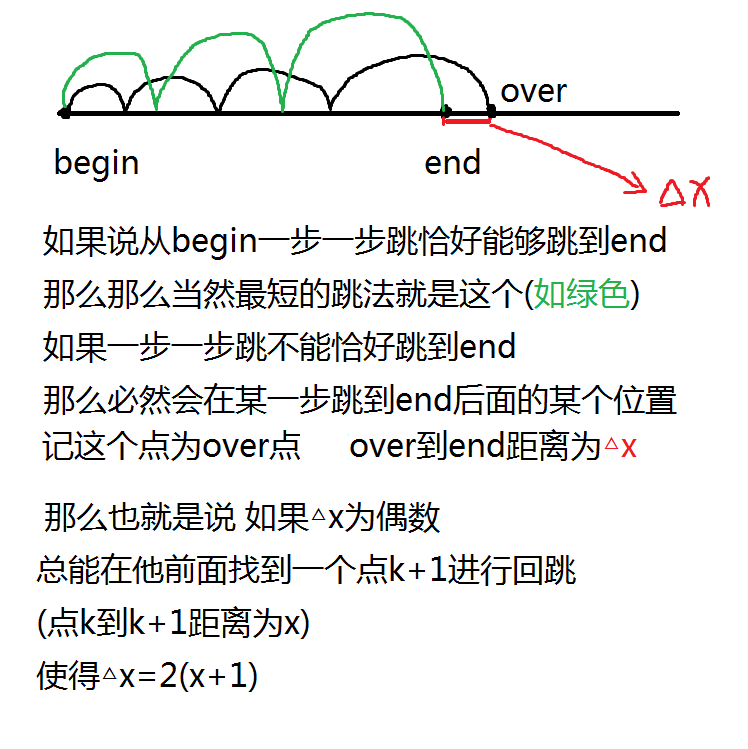
如果超过n的距离是一个奇数,那么我们则需要先把他处理成一个偶数,再在中间的某个步骤中回跳一次。那么如何处理呢?
处理方法是接着往右跳,拉大与n的距离,当与n的距离变为一个偶数时遍可以转化为上一种情况。
实际上只需要往右跳1步(接下来跳的步数是奇数)数或者2步(接下来跳的步数是偶数),下面是图片分析:

下面是具体代码实现:

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main(){ 4 int x; 5 scanf("%d",&x); 6 if (x < 0)x = -x; 7 if (x == 0) printf("0 "); 8 else{ 9 int step = 1,pos = 0,cnt = 0; 10 while (pos < x){ 11 pos += step++; 12 cnt++; 13 } 14 if (pos==x) printf("%d ",cnt); 15 else if ((pos-x)%2==0) printf("%d ",cnt); 16 else{ 17 if ((pos-x+step)%2==0) printf("%d ",cnt+1); 18 else printf("%d ",cnt+2); 19 } 20 } 21 return 0; 22 }
