51Nod

给出一个n，求1-n这n个数，同n的最小公倍数的和。
例如：n = 6，1,2,3,4,5,6 同6的最小公倍数分别为6,6,6,12,30,6，加在一起 = 66。

由于结果很大，输出Mod 1000000007的结果

 

ai <= 1e9

 

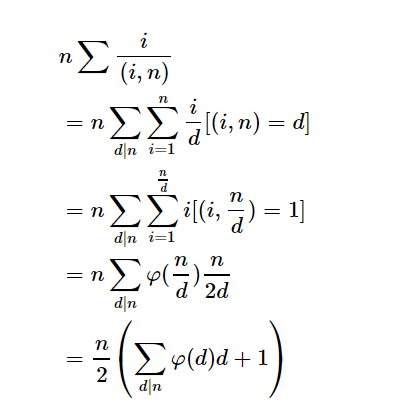
 公式推导如上。

最后只需要预处理出质因子，用积性函数的性质在线处理即可。

#pragma warning(disable:4996)

#include<iostream>
#include<algorithm>
#include<bitset>
#include<tuple>
#include<unordered_map>
#include<fstream>
#include<iomanip>
#include<string>
#include<cmath>
#include<cstring>
#include<vector>
#include<map>
#include<set>
#include<list>
#include<queue>
#include<stack>
#include<sstream>
#include<cstdio>
#include<ctime>
#include<cstdlib>
#define INF 0x3f3f3f3f
#define inf 0x7FFFFFFF
#define MOD 1000000007
#define moD 1000000003
#define pii pair<int,string>
#define eps 1e-8
#define equals(a,b) (fabs(a-b)<eps)
#define bug puts("bug")
#define re  register
#define fi first
#define se second
const int maxn = 1e6 + 5;
const double Inf = 10000.0;
const double PI = acos(-1.0);
typedef  long long ll;
typedef unsigned long long ull;
using namespace std;

int prime[maxn];
int vis[maxn];
int cnt;

int euler_sieve(int n) {
    for (int i = 2; i <= n; i++) {
        if (!vis[i]) prime[cnt++] = i;
        for (int j = 0; j < cnt; j++) {
            if (i * prime[j] > n) break;
            vis[i * prime[j]] = 1;
            if (i % prime[j] == 0) break;
        }
    }
    return cnt;
}


ll quickPower(ll a, ll b, ll m) {
    ll base = a;
    ll ans = 1;
    while (b) {
        if (b & 1) {
            ans *= base;
            ans %= m;
        }
        base *= base;
        base %= m;
        b >>= 1;
    }
    return ans;
}

ll inv2;

ll solve(ll n) {
    ll ans = 1;
    for (int i = 0; prime[i] * prime[i] <= n && i <= cnt; i++) {
        if (n % prime[i] == 0) {
            ll now = 1ll, sum = 1ll;
            while (n % prime[i] == 0) {
                n /= prime[i];
                now *= prime[i];
                sum += (now - now / prime[i]) * now;
            }
            ans = ans * sum % MOD;
        }
    }
    if (n > 1) ans = ans * (1ll + n * (n - 1) % MOD) % MOD;
    return ans + 1ll;
}

int main() {
    euler_sieve(40000);
    int T;
    inv2 = quickPower(2ll, MOD - 2, MOD);
    scanf("%d", &T);
    while (T--) {
        ll n;
        scanf("%lld", &n);
        printf("%lld
", solve(n) * (n * inv2 % MOD) % MOD);
    }
}