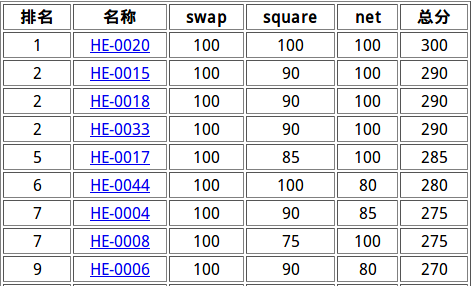
诶一看这不是水题AK场吗?然后80分钟就拿到了285分。
然后,对拍?还是卡T2常数?还是想T2正解?
于是上述三项我依次进行了。
前两项让我的分数丝毫不变但是吃掉了我一个多小时的时间。
卡常卡的也不彻底,不然就能再多个5分。因为心里还想着我想想正解。
最后剩余不多的时间里想到了一个接近正解的思路。。。因为没有时间写所以也就放弃了进一步的思考。
首先肯定还是要%%%Paris值得纪念的考试。
然后至于我。。。现在真的是水题考不高,难题不会做。。。
没前途。联赛啊。。。省选啊。。。不要止步于此啊。。。
T1:字符交换
二分答案。枚举从哪个字符开始。
最优决策一定是聚拢到最中间的那个字符的位置。
前缀和+等差数列求和就可以把绝对值拆掉。
总复杂度$O(nlogn)$

1 #include<cstdio> 2 #include<vector> 3 using namespace std; 4 vector<int>v[26]; 5 char s[4005];int n,k,tot[26][4005]; 6 int cal(int l,int r){return (l+r)*(r-l+1)/2;} 7 int tp(int i,int l,int r){return tot[i][r]-tot[i][l-1];} 8 bool chk(int len){ 9 for(int i=0;i<26;++i)if(v[i].size()>=len)for(int j=1;j+len-1<=v[i].size();++j){ 10 int l=j,r=j+len-1,m=j+(len>>1),mp=v[i][m-1]; 11 if(-tp(i,l,m)+cal(mp-m+l,mp)+tp(i,m+1,r)-cal(mp+1,mp+r-m)<=k)return true; 12 } 13 return false; 14 } 15 int main(){freopen("swap.in","r",stdin);freopen("swap.out","w",stdout); 16 scanf("%d%d%s",&n,&k,s+1); 17 for(int i=1;i<=n;++i)v[s[i]-'a'].push_back(i); 18 for(int i=0;i<26;++i)for(int j=0;j<v[i].size();++j)tot[i][j+1]=tot[i][j]+v[i][j]; 19 int l=1,r=n,ans; 20 while(l<=r)if(chk(l+r>>1))ans=l=l+r>>1,l++;else r=(l+r>>1)-1; 21 printf("%d ",ans); 22 }
T2:平方数
如果一个数含有平方因子,那么把它干掉之后这个数与其它数的关系不变。
于是筛出$sqrt{1e9}$以内的所有质数(4300个左右),用它干掉所有平方因子,然后哈希表统计答案。
复杂度$O(4000n)$,能得到$70~90$不等。

1 #include<cstdio> 2 #include<cmath> 3 using namespace std; 4 struct hash_map{ 5 int fir[2000005],l[300005],to[300005],w[300005],cnt; 6 int &operator[](int x){ 7 int r=x%2000003; 8 for(int i=fir[r];i;i=l[i])if(to[i]==x)return w[i]; 9 l[++cnt]=fir[r];fir[r]=cnt;to[cnt]=x;return w[cnt]; 10 } 11 }M; 12 int al[33333],cnt,p[4444],n,q[4444];long long ans; 13 int main(){freopen("square.in","r",stdin);freopen("square.out","w",stdout); 14 for(int i=2;i<=1000;++i)if(!al[i]){ 15 p[++cnt]=i; 16 for(int j=2;j*i<=1000;++j)al[i*j]=1; 17 } 18 for(int i=1;i<=cnt;++i)q[i]=p[i]*p[i]; 19 q[++cnt]=1000000007; 20 scanf("%d",&n); 21 while(n--){ 22 int x,y=1;scanf("%d",&x); 23 for(int i=1;x>=q[i];++i){ 24 while(x%q[i]==0)x/=q[i]; 25 if(x%p[i]==0)x/=p[i],y*=p[i]; 26 } 27 int q=sqrt(x);if(q*q!=x)y*=x; 28 int &P=M[y];ans+=P;P++; 29 }printf("%lld ",ans); 30 }
进一步优化这个思路,$sqrt{1e9}$显然就是复杂度瓶颈。
考虑如何能够不筛那么多。
对于每一个数,它含有超过1000的平方因子至多有1个($1000^2=1000000$,放不下两个)
那么把它们都筛一遍是多余的。
那么就筛到1000,考虑剩下的是什么。
改变筛的策略,对于你枚举的1000以内的数时,不止干掉平方因子,单个一次的因子也干掉(但是要记录下来累乘到一个变量y里)
最后剩下的数,对它进行质因数分解,它的最小因子也大于1000。而且它之可能是以下4种情况:
- 是一个平方数
- 是两个大于1000的质数相乘
- 是一个大于1000的质数
- 是1
继续上面的思路,我们只需要干掉它的平方因子。
因为现在它不可能是平方数×另一个数的形式,所以我们直接开根判断它是不是平方数。
如果是就干掉,否则剩余的部分也累乘到y里。
那么y就是原数干掉所有平方因子之后所剩下的。
1000以内的质因子只有170个。总复杂度$O(170n)$
(cbx实践证明,就算你不用质数筛而是1000个全筛$O(1000n)$也是能AC的,但是在老年评测机下就不一定了)

1 #include<cstdio> 2 #include<cmath> 3 using namespace std; 4 struct hash_map{ 5 int fir[2000005],l[300005],to[300005],w[300005],cnt; 6 int &operator[](int x){ 7 int r=x%2000003; 8 for(int i=fir[r];i;i=l[i])if(to[i]==x)return w[i]; 9 l[++cnt]=fir[r];fir[r]=cnt;to[cnt]=x;return w[cnt]; 10 } 11 }M; 12 int al[33333],cnt,p[4444],n,q[4444];long long ans; 13 int main(){freopen("square.in","r",stdin);freopen("square.out","w",stdout); 14 for(int i=2;i<=1000;++i)if(!al[i]){ 15 p[++cnt]=i; 16 for(int j=2;j*i<=1000;++j)al[i*j]=1; 17 } 18 for(int i=1;i<=cnt;++i)q[i]=p[i]*p[i]; 19 q[++cnt]=1000000007; 20 scanf("%d",&n); 21 while(n--){ 22 int x,y=1;scanf("%d",&x); 23 for(int i=1;x>=q[i];++i){ 24 while(x%q[i]==0)x/=q[i]; 25 if(x%p[i]==0)x/=p[i],y*=p[i]; 26 } 27 int q=sqrt(x);if(q*q!=x)y*=x; 28 int &P=M[y];ans+=P;P++; 29 }printf("%lld ",ans); 30 }
T3:多维网络
部分分给的很全啊。
首先最基本的就是有$n$种物品每种有$a_i$个那么本质不同的排列数是$frac{(sumlimits_{i=1}^{n} a_i)!}{prodlimits_{i=1}^{n}a_i!}$
观察部分分提示,n=0的直接就是套式子。
n=1需要去掉经过了这个点的路径,那么就计算一下经过这个点的路径有多少,其实就是把路径拆成了两部分,相乘即可。
n=2的话也一样啊,只不过要去掉两种经过了这两个点之一的路径,但是减多了,还要加回来两个点都经过了的路径。
n=3。。。
这不就是容斥么???
但是在n=500时,手动容斥估计码长都能超限。
运用一些性质,每个点只会走到各坐标都比它大的点。我们把这样的关系连边。然后边权就是从一个点走到另一个点的方案数,套上面的式子。
然后就可以得到一个DAG。(当然没有环。。。)。DAG?当然拓扑啦。
然后这个容斥说白了就是奇加偶减,考虑奇偶。
就是如果路径上有奇数个点,那么答案加这么多,否则减。
初始状态是在原点,偶数步方案数为1,奇数步方案数为0。
然后跑拓扑,按照边权统计方案。
最后输出终点的奇数步-偶数步就是答案。
在有重复点的时会出锅(DAG有环),我判掉了不知道有没有用。。。

1 #include<cstdio> 2 #define mod 1000000007 3 int n,d,x[105][505],fac[10000005],inv[10000005],dp[2][505]; 4 int fir[505],l[250005],to[250005],w[250005],deg[505],ec,q[505]; 5 int qpow(long long b,int t,long long a=1){for(;t;t>>=1,b=b*b%mod)if(t&1)a=a*b%mod;return a;} 6 bool com(int p1,int p2){ 7 for(int i=1;i<=d;++i)if(x[i][p1]>x[i][p2])return false; 8 return true; 9 } 10 bool sam(int p1,int p2){ 11 for(int i=1;i<=d;++i)if(x[i][p1]!=x[i][p2])return false; 12 return true; 13 } 14 void Swap(int p1,int p2){ 15 for(int i=1;i<=d;++i)x[i][p1]^=x[i][p2]^=x[i][p1]^=x[i][p2]; 16 } 17 int cal(int p1,int p2){ 18 int tot=0,ans; 19 for(int i=1;i<=d;++i)tot+=x[i][p2]-x[i][p1]; 20 ans=fac[tot]; 21 for(int i=1;i<=d;++i)ans=1ll*ans*inv[x[i][p2]-x[i][p1]]%mod; 22 return ans; 23 } 24 void link(int a,int b,int v){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;w[ec]=v;deg[b]++;} 25 main(){freopen("net.in","r",stdin);freopen("net.out","w",stdout); 26 fac[0]=1; 27 for(int i=1;i<=10000000;++i)fac[i]=1ll*fac[i-1]*i%mod; 28 inv[10000000]=qpow(fac[10000000],mod-2); 29 for(int i=9999999;~i;--i)inv[i]=inv[i+1]*(i+1ll)%mod; 30 scanf("%d%d",&d,&n);n++; 31 for(int i=1;i<=d;++i)scanf("%d",&x[i][n]); 32 for(int i=1;i<n;++i)for(int j=1;j<=d;++j)scanf("%d",&x[j][i]); 33 for(int i=1;i<n;++i)for(int j=i+1;j<n;++j)if(sam(i,j))Swap(j,n-1),Swap(n-1,n),n--; 34 for(int i=0;i<=n;++i)for(int j=0;j<=n;++j)if(i!=j&&com(i,j))link(i,j,cal(i,j)); 35 dp[0][0]=1; 36 for(int h=1,t=1;h<=t;++h){ 37 int p=q[h]; 38 for(int i=fir[p];i;i=l[i]){ 39 deg[to[i]]--; 40 if(!deg[to[i]])q[++t]=to[i]; 41 dp[1][to[i]]=(dp[1][to[i]]+1ll*dp[0][p]*w[i])%mod; 42 dp[0][to[i]]=(dp[0][to[i]]+1ll*dp[1][p]*w[i])%mod; 43 } 44 } 45 printf("%d ",(dp[1][n]-dp[0][n]+mod)%mod); 46 }
