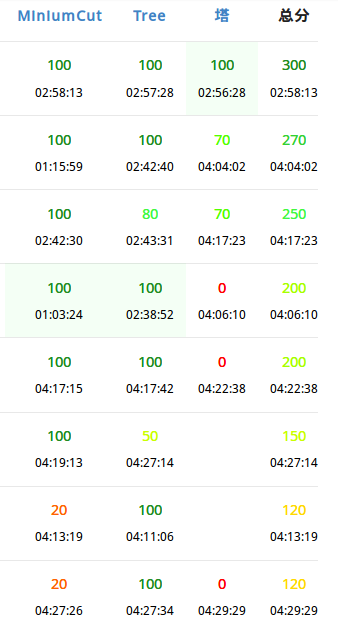

今天的题貌似相对比较简单?
$T1$只要发现是个最短路树就完事了。
$T2$是一个做烂了的$dp$。上次我的确不会(虽说对于当时而言,也已经做烂了然而我还是不会)
反正这次要是再不会就不合适了。
$T3$就是个睿智。。。

结果还读错题,连暴力分都挂没了。
样例水坑人啊。。。
T1:MiniumCut
大意:给出$n$个点两两之间的最小割,构造一个满足它的图。$n le 100,w_{i,j}$
两两之间最小割,显然最小割树。
那么题意变为:构造一棵树,满足$f(i,j)=w_{i,j}$其中$f(i,j)$表示树上路径中最小的边。
从大到小枚举边权,不断加边,一定满足:某一种权值加完后,整个图中每个联通块都是完全图。
并查集维护边数点数。$O(n^2)$

1 #include<bits/stdc++.h> 2 using namespace std; 3 int w[105][105],ansx[105],ansy[105],answ[105],n,cnt,f[105],sz[105],e[105]; 4 int find(int p){return f[p]==p?p:f[p]=find(f[p]);} 5 vector<int>vx[100005],vy[100005]; 6 int main(){ 7 cin>>n; 8 for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)scanf("%d",&w[i][j]); 9 for(int i=1;i<=n;++i)for(int j=i+1;j<=n;++j) 10 if(w[i][j]==w[j][i]&&w[i][j])vx[w[i][j]].push_back(i),vy[w[i][j]].push_back(j); 11 else return puts("-1"),0; 12 for(int i=1;i<=n;++i)f[i]=i,sz[i]=1; 13 for(int i=100000;i;--i)if(vx[i].size()){ 14 for(int j=0;j<vx[i].size();++j){ 15 int x=vx[i][j],y=vy[i][j]; 16 if(find(x)==find(y))e[f[x]]++; 17 else x=f[x],y=f[y],f[x]=y,sz[y]+=sz[x],e[y]+=e[x]+1,ansx[++cnt]=x,ansy[cnt]=y,answ[cnt]=i; 18 } 19 for(int j=1;j<=n;++j)if(f[j]==j&&e[j]!=sz[j]*(sz[j]-1)>>1)return puts("-1"),0; 20 } 21 printf("%d ",n-1); 22 for(int i=1;i<n;++i)printf("%d %d %d ",ansx[i],ansy[i],answ[i]); 23 }
T2:Tree
大意:边权树,选出互不相同的$k$个点构成排列$A_{1...k}$,最小化$sumlimits_{i=1}^{k-1} dis(A_i ,A_{i+1})$。$n le 3000$
这式子相当与从树上挨个点走,如果再加上$dis(A_k,A_1)$那就是回路了。
所以这就是让你选出$k$个点,求回路去掉直径的最小值。
你显然会选一个联通块。所以可以直接子树归并的$dp$
经典的树$dp$。$dp[0/1/2][p][x]$表示当前已选中$x$个点,在$p$子树中:尚未考虑直径/已经确定直径一个端点且$p$就在直径上/整个直径已经确定 时的最小值。
转移比较简单。$O(nk)$

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define S 3003 4 int dp[3][S][S],sz[S],fir[S],l[S<<1],to[S<<1],w[S<<1],ec,n,k,t[3][S],ans=0x3fffffff; 5 void link(int a,int b,int W){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;w[ec]=W;} 6 void dfs(int p,int fa){ 7 sz[p]=1; 8 for(int i=fir[p],y;y=to[i];i=l[i])if(y!=fa){ 9 dfs(y,p); 10 for(int x=0;x<=sz[p]+sz[y]&&x<=k;++x)t[0][x]=t[1][x]=t[2][x]=0x3fffffff; 11 for(int a=0;a<=2;++a)for(int b=0;a+b<=2;++b)for(int x=1;x<=sz[p]&&x<=k;++x)for(int z=0;z<=sz[y]&&x+z<=k;++z) 12 t[a+b][x+z]=min(t[a+b][x+z],dp[a][p][x]+dp[b][y][z]+(z?(b!=1?w[i]<<1:w[i]):0)); 13 sz[p]+=sz[y]; 14 for(int x=1;x<=sz[p]&&x<=k;++x)for(int a=0;a<3;++a)dp[a][p][x]=t[a][x]; 15 } 16 } 17 int main(){ 18 scanf("%d%d",&n,&k); 19 for(int i=1,a,b,W;i<n;++i)scanf("%d%d%d",&a,&b,&W),link(a,b,W),link(b,a,W); 20 dfs(1,0); 21 for(int i=1;i<=n;++i)if(sz[i]>=k)ans=min(ans,dp[2][i][k]); 22 cout<<ans<<endl; 23 }
T3:塔
大意:维护字符串支持在首/尾添加一个字符,撤销最后几次填字符的操作,每次操作后回答最长回文子串长。$q le 10^7$
首先学到了两件事:
原来$PAM$可以支持双端加字符啊。
原来$hash$可以支持双端加字符啊。
然后这题没了。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define S 10000005 4 #define mod 1000000007 5 int qp(int b,int t,int a=1){for(;t>>=1;b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a;} 6 int t,h,q,la,d[S],ope,ans[S],hsh[S<<1],ihsh[S<<1],pw[S]; char s[S*3]; 7 short c[S<<1];long long tot; const long long iv=qp(131,mod-2); 8 int mo(int x){return x>=mod?x-mod:x;} 9 int Hsh(int l,int r){return mo(hsh[r]-1ll*hsh[l-1]*pw[r-l+1]%mod+mod);} 10 int Ihsh(int l,int r){return mo(ihsh[l]-1ll*ihsh[r+1]*pw[r-l+1]%mod+mod);} 11 bool ispalin(int l,int r){return h<=l&&r<=t&&Hsh(l,r)==Ihsh(l,r);} 12 int main(){ 13 h=10000001;t=10000000;scanf("%d",&q); 14 for(int i=pw[0]=1;i<=q;++i)pw[i]=pw[i-1]*131ll%mod; 15 gets(s); gets(s); 16 for(int _=0;_<q;++_){ 17 int op=s[_*3]-48,v=((s[_*3+1]-48)*10+s[_*3+2]-48+la)%100; 18 if(op==1){ 19 c[++t]=v; hsh[t]=(hsh[t-1]*131ll+v)%mod; d[++ope]=0; 20 ihsh[t]=(ihsh[t-1]-c[t-1]+mod)*iv%mod; 21 ihsh[t+1]=(ihsh[t]-c[t]+mod)*iv%mod; 22 if(ispalin(t-la-1,t))la+=2;else if(ispalin(t-la,t))la++; 23 }else if(op==2){ 24 c[--h]=v; ihsh[h]=(ihsh[h+1]*131ll+v)%mod; d[++ope]=1; 25 hsh[h]=(hsh[h+1]-c[h+1]+mod)*iv%mod; 26 hsh[h-1]=(hsh[h]-c[h]+mod)*iv%mod; 27 if(ispalin(h,h+la+1))la+=2;else if(ispalin(h,h+la))la++; 28 }else{ while(v--)if(d[ope--])h++;else t--; la=ans[t-h+1]; } 29 tot+=la;ans[t-h+1]=la; 30 ihsh[t+1]=(ihsh[t]-c[t]+mod)*iv%mod; 31 hsh[h-1]=(hsh[h]-c[h]+mod)*iv%mod; 32 }cout<<tot<<endl; 33 }
