最小割树
利用一张图的不同割最多只有n-1种(我不会证)
利用分治的做法,在l,r区间任意选取两点进行全局最小割,然后把l,r区间分成S,T两个区域(以割边为界限),分别进行递归,递归前要把流量复原保证每次进行的都是全局的最小割。

#include<bits/stdc++.h> #define N 855 #define M 17005 #define inf 0x3f3f3f3f using namespace std; int n,m,S,T,B,ans,head[N],cur[N],dep[N],to[M],nxt[M],flo[M],rec[M],ord[N],tmp[N],vis[N]; map <int,int> Map; inline int rd(){ register int x=0,f=1;char ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+ch-48,ch=getchar(); return x*f; } void lnk(int x,int y,int flow){ to[++B]=y,nxt[B]=head[x],head[x]=B,flo[B]=rec[B]=flow; to[++B]=x,nxt[B]=head[y],head[y]=B,flo[B]=rec[B]=flow; } bool bfs(){ memset(dep,0,sizeof dep); queue <int> q; dep[S]=1; cur[S]=head[S]; q.push(S); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=nxt[i]) if(flo[i]&&!dep[to[i]]){ dep[to[i]]=dep[u]+1; cur[to[i]]=head[to[i]]; if(to[i]==T) return 1; q.push(to[i]); } }return 0; } int dfs(int u,int cup){ if(u==T) return cup; int res=cup,v; for(int &i=cur[u];i;i=nxt[i]) if(flo[i]&&dep[to[i]]==dep[u]+1){ v=dfs(to[i],min(res,flo[i])); if(!v) dep[to[i]]=0; else res-=v,flo[i]-=v,flo[i^1]+=v; if(!res) break; }return cup-res; } void Dfs(int x){ vis[x]=1; for(int i=head[x];i;i=nxt[i]) if(flo[i]&&!vis[to[i]]) Dfs(to[i]); } void solve(int l,int r){ if(l>=r) return; S=ord[l]; T=ord[l+1]; int maxflow=0; while(bfs()) maxflow+=dfs(S,inf); if(!Map[maxflow]) ans++; Map[maxflow]=1; memset(vis,0,sizeof vis); Dfs(S); int itl=l-1,itr=r+1; for(int i=l;i<=r;++i) if(vis[ord[i]]) tmp[++itl]=ord[i]; else tmp[--itr]=ord[i]; for(int i=l;i<=r;++i) ord[i]=tmp[i]; memcpy(flo,rec,sizeof flo); solve(l,itl); solve(itr,r); } int main(){ n=rd(); m=rd(); B=1; for(int i=1,x,y,z;i<=m;++i) x=rd(),y=rd(),z=rd(),lnk(x,y,z); for(int i=1;i<=n;++i) ord[i]=i; solve(1,n); printf("%d ",ans); return 0; }
vim的查找与替换
vimrc里填上一句set hlsearch,然后在平时输入:wq的地方输入:/x就能查找x。
在平时输入:wq的地方输入:%s/X/Y/g就能查找把所有X替换成Y。
最小表示法
一个字符串O(n)找到循环同构的字典序最小的字符串的方法。设B[i]表示以第i个字符开始的字符串。
把自己复制成两倍,然后两个指针i=1,j=2,这里我们必须保证何时都要有i!=j,要不然自己跟自己肯定就是相等的了。
然后设从i,j开始最长匹配长度是k(这里我们的k位置的字符是不匹配的,即s[i+k]!=s[j+k]),假设s[i+k]<s[j+k]。
那么肯定的是B[j]不是最小表示了,同时可以肯定的是B[j]~B[j+k]都不是最小表示了,因为相应的B[i]~B[i+k]开始的字符串肯定更小啊。

#include<bits/stdc++.h> #define N 600005 using namespace std; int n,s[N]; inline int rd(){ register int x=0,f=1;char ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+ch-48,ch=getchar(); return x*f; } int main(){ n=rd(); for(int i=1;i<=n;++i) s[i]=s[n+i]=rd(); int i=1,j=2,k; while(i<=n&&j<=n){ for(k=0;k<=n&&s[i+k]==s[j+k];k++); if(k==n) break; if(s[i+k]>s[j+k]){ i=i+k+1; if(i==j) ++i; } else{ j=j+k+1; if(i==j) ++j; } } int st=min(i,j); for(int i=1;i<=n;++i) printf("%d ",s[st+i-1]); return 0; }
基数排序
对十进制每一位进行排序的一种排序做法。复杂度为O(最大位数×n)
开个10的桶,从低位到高位按照数字从小到大排序,再把这些收集起来进行下一位的排序。
原根
原根,是一个数学符号。设m是正整数,a是整数,若a模m的阶等于φ(m),则称a为模m的一个原根。
阶的定义:对于模数m和底数a来说,使得$a^b=1 mod m$的最小正整数b叫做a模m的阶。
又因为$a^{phi(m)}=1 mod m$,因此$b | phi(m)$。
也就是阶只有可能是$phi(m)$的约数。
原根的充要条件是$m=2,4,p^e,2p^e$,其中p是奇质数,e是正整数
小定理:任何一个素数的原根个数是$phi(m-1)$
原根的求法:对与$phi(m)$质因数分解$p_1^{c_1},p_2^{c_2}...$,如果$g$是原根,那么对于任意的$i$,都有$g^{frac{phi(m)}{p_i}} eq 1$$ (mod m)$
实战:记得快速幂时候的模数并不是原题中方案数,而是质数m;是对$phi(m)$质因数分解,而不是m
分治FFT
用于求解一种类似于f[i]=$sum$f[i-k]*g[k]的算法,与普通FFT不同的是需要用到这个序列的前面的数。$O(n*log^2)$
首先递归求解左半段(l,mid),然后FFT处理出左半段对右半段的贡献并加进右半段里,然后递归处理右半段
泰勒展开的个人理解
泰勒展开式具有广泛的应用,它犹如一把倚天剑可以纵横挥洒,一剑封喉。
$f(x)=sumlimits_{i=0}^{n}frac{f^{(i)}(x_0)(x-x_0)^i}{i!}$
我们要求得x=x时的f(x)值,但不好求怎么办,考虑用离x很近的x0进行拼凑,用导数(相当于是变化率)乘上横坐标的变化量的次幂(与导数相对)就是纵坐标的相应变化量。
线性筛约数和
$i\%p==0->f_{i*p}=f_i*f_p-f_{i/p}*p$
$i\%p!=0->f_{i*p}=f_i*f_p$
线性筛约数个数
$i\%p==0->f_{i*p}=2*f_i-f_{i/p}$
$i\%p!=0->f_{i*p}=f_i*f_p$
本来没打算学下面几个知识点,只不过sa不会->sam不会->suffix tree不会->pat不会->笛卡尔树不会->又看到了约束(标准)RMQ不会->自闭看了一上午
sa/sam/suffix tree 老师锅给DC讲了,我不打算写。
笛卡尔树
每个点有两个关键字:下标和权值,下标有满足二叉搜索树性质,权值满足堆。建树O(N)
具体做法:按下标升序,设当前插入值是v3。用单调栈维护整棵树的最右链,一路pop找到比它小的第一个值v1。
因为v1是比它小的第一个值,所以v1的右儿子v2一定大于等于v3,所以把v2设成v3左儿子(下标小,权值大),v3设成v1的右儿子(下标大,权值大)
注意没有v2的情形,即v1是叶子;注意没有v1的情形,即v3是新根

#include<bits/stdc++.h> using namespace std; const int N=1e5+50; int n,v[N],prt[N],ls[N],rs[N]; int stk[N],top; int main(){ scanf("%d",&n); for(int i=1;i<=n;++i){ scanf("%d",&v[i]); while(top&&v[stk[top]]>=v[i]) ls[i]=s[top--]; if(top) prt[i]=stk[top],rs[stk[top]]=i; if(ls[i]) prt[ls[i]]=i; s[++top]=i; } return 0; }
约束(标准)RMQ(±1RMQ)
一种预处理O(N)查询O(1)的算法。
前提条件是两项之差最大为1。
这个可以用欧拉序来保证,相邻点深度差一定为1,至于序列上怎么办,就需要转成笛卡尔树,然后区间(l,r)最小值就是lca(l,r)。应该好理解吧。
现在原序列RMQ转化为求欧拉序上某段区间深度的最小值,满足了约束RMQ的条件。
原序列分块,块内预处理,块间做ST表
对欧拉序分块,大小L=log(n)/2,块数D=n/L,对块块做ST表复杂度O(Dlog(D))=O(n/L(logn-logL))=O(n/L*L)=O(n)
考虑利用标准RMQ的性质,本质不同的块一共只有$2^L=sqrt n$种,枚举每一种块处理出来最小值以及01序列(增量+1为1,-1为0),复杂度O($frac{sqrt nlog(n)}{2}$)<O(n)
之所以这样,是为了保证查询O(1)不能有边角的枚举。
对于询问时,大块ST表O(1),边角找到对应的01序列根据之前预处理出来的数组(长度<L就把后面都置为1保证最小解不会出现在后面)直接找到最小值再加上偏移量就是答案。
感觉很不好打,万一就卡O(nlogn)的RMQ呢(手动滑稽
suffix tree
trie的简化版几条边合并一下,把每个点维护一个字符变成维护[l,r]一段区间。
因为要保证每个后缀都要出现,因此要在最后加一个'$'
解决最长回文:获取LCA(s(i),s'(n-i+1)),LCA(s(i+1),s'(n-i+1))(可暂时不会预处理LCA啊)
查找子串:直接在树上搜索子串,因为子串一定是某个后缀的前缀
查找T在串里的重复次数:用S+$构造后缀树,T节点下的叶子节点就是重复次数,同查找子串
找最长重复子串:就是找到最深的非叶节点,即有一个以上的叶子节点,同上
两个子串的最长公共部分:将S1#S2$
作为字符串压入后缀树,找到最深的非叶节点,且该节点的叶节点既有#也有$(无#)。(不确定)
还有一种方法:将S1$,S2#压入后缀树找出最深的同时属于两个串的节点,从根到这个节点就是lcs。
建树有O(N)的我看不懂啊,O($N^3?$)也不愿意打...
约数个数表
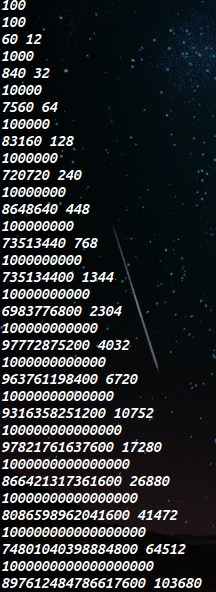
倍增并查集
对每个位置开$log$个点$fa[i][j]$表示以$i$开头的长度为$1<<j$这么一段区间的开头的代表是谁。
那么显然开始时$f[i][j]=i$。
对于$[l1,r1],[l2,r2]$两段区间要求合并并查集,就可以把$r1-l1+1$取$Logg$然后合并$(l1,l2,Logg)$,$r1-(1<<Logg)+1,r2-(1<<Logg)+1,Logg)$。
怎么统计答案是件值得思考的事,看代码下。
1 for(int i=Log[n];i;--i) 2 for(int j=1;j+(1<<i)-1<=n;++j){ 3 int x=find(j,i); 4 merge(x,j,i-1); 5 merge(x+(1<<i-1),j+(1<<i-1),i-1); 6 }
把区间从大到小合并,$f[j][i]$的开头代表是$x$的话,就意味着$[j,i+(1<<i)-1],[x,x+(1<<i)-1]$是合并起来的。
那么就把$[j,j+(1<<i-1)-1],[x,x+(1<<i-1)-1]$合并,$[j+(1<<i-1),j+(1<<i)-1],[x+(1<<i-1),x+(1<<i)-1]$合并,起到的作用是等价的。
 scoi2016萌萌哒
scoi2016萌萌哒exlucas
用于求解$C_n^m$%mod而mod不是质数的情况。
如果mod所有因子指数都是1也可以用直接计算每个质因子作为模数的答案直接CRT合并,但不是的话就只能用exlucas了。
exlucas用的也是CRT,只是模数是$p^k$,$p^k$是mod的唯一分解定理出来的质因子。
计算$C_n^m$对每个$p^k$取模的结果,由于$p^k$互质,再将所有答案用CRT合并即可得到原解。
问题转化为求$n!$%$p^k$的答案,先$nlogn$处理出$n!$中包含的所有p因子,接着计算$frac{n!}{p^a}$对$p^k$取模的结果。
我们知道在%$p^k$意义下$prod limits_{i=1}^{p^k-1}=prod limits_{i=p^k+1}^{2p^k-1}$
把所有p都提取出来后,那么n!就可以分成三种数:$p^{frac{n}{p}}$,$frac{n}{p}!$,和$p^k$内与p互质的数的乘积。
这样的$p^k$积一共循环了$frac{n}{p^k}$次,直接快速乘上去,还有一段长度为n%$p^k$的积暴力乘上去就好了。
复杂度与$p^k$的k有关。
记得预处理$p^k$的积

#include<bits/stdc++.h> #define ll long long using namespace std; int T,mod,n,n1,n2,m,num[10]; int c[10],p[10],pw[10],ycl[10],o; void exgcd(ll a,ll b,ll &x,ll &y){ if(!b){x=1;y=0;return;} exgcd(b,a%b,y,x); y-=(a/b)*x; } ll mgml(ll a,ll b,ll mo,ll ans=1){ for(;b;b>>=1,a=a*a%mo) if(b&1) ans=ans*a%mo; return ans; } ll fac(ll x,ll u){ if(x==0) return 1; ll jzoj=mgml(ycl[u],x/pw[u],pw[u]); for(int i=1;i<=x%pw[u];++i) if(i%p[u]) jzoj=jzoj*i%pw[u]; return fac(x/p[u],u)*jzoj%pw[u]; } ll inv(ll a,ll u){ ll b=pw[u],x,y; exgcd(a,b,x,y); return (x%pw[u]+pw[u])%pw[u]; } ll exLucas(ll x,ll y,ll u){//C(x,y) ll f1=fac(x,u),f2=fac(y,u),f3=fac(x-y,u); int cnt=0; for(ll i=p[u];i<=x;i=i*p[u]) cnt+=x/i; for(ll i=p[u];i<=y;i=i*p[u]) cnt-=y/i; for(ll i=p[u];i<=x-y;i=i*p[u]) cnt-=(x-y)/i; return mgml(p[u],cnt,pw[u])*f1%pw[u]*inv(f2,u)%pw[u]*inv(f3,u)%pw[u]; } ll CHR(ll x,ll y){//C(x,y) if(x<y||y<0) return 0; ll ans=0; for(int u=1;u<=o;++u){ ll sx,sy;exgcd(mod/pw[u],pw[u],sx,sy); ans=(ans+exLucas(x,y,u)*mod/pw[u]%mod*sx%mod+mod)%mod; } return (ans%mod+mod)%mod; } int main(){ scanf("%d%d",&T,&mod); int uoj=mod; for(int i=2;i*i<=uoj;++i) if(uoj%i==0){ p[++o]=i; while(uoj%i==0) uoj/=i,c[o]++; } if(uoj!=1) p[++o]=uoj,c[o]=1; for(int i=1;i<=o;++i) for(int j=pw[i]=1;j<=c[i];++j) pw[i]*=p[i]; for(int i=1;i<=o;++i) for(int j=ycl[i]=1;j<pw[i];++j) if(j%p[i]) ycl[i]=1ll*ycl[i]*j%pw[i]; while(T--){ scanf("%d%d%d%d",&n,&n1,&n2,&m); for(int i=0;i<n1;++i) scanf("%d",&num[i]); for(int i=0,x;i<n2;++i) scanf("%d",&x),m-=x-1; if(m<0) {puts("0");continue;} int U=1<<n1; ll ans=0; for(int i=0;i<U;++i){ int cc=0,bzoj=m; for(int j=0;j<n1;++j) if(i&(1<<j)) ++cc,bzoj-=num[j]; ans=(ans+(cc&1?-1ll:1ll)*CHR(bzoj-1,n-1))%mod; } printf("%lld ",(ans%mod+mod)%mod); } return 0; }

#include<bits/stdc++.h> #define LL long long #define int long long #define max(a,b) ((a)>(b)?(a):(b)) #define min(a,b) ((a)>(b)?(b):(a)) using namespace std; int read(); LL P,n,m,tmp,cnt,w[6]; LL c[25],p[25],pw[25]; void exgcd(LL x,LL y,LL &a,LL &b){ if(!y){a=1;b=0;return;} exgcd(y,x%y,b,a); b-=x/y*a; } LL mgml(LL a,LL b,LL p,LL ans=1){ for(;b;b>>=1,a=a*a%p) if(b&1) ans=ans*a%p; return ans; } LL inv(LL x,LL mod){ LL a,b;exgcd(x,mod,a,b); return (a+mod)%mod; } LL fac(LL x,LL p,LL pw,LL ans=1){if(!x) return 1; for(int i=1;i<pw;++i) if(i%p) ans=ans*i%pw; ans=mgml(ans,x/pw,pw); for(LL i=1,_E_=x%pw;i<=_E_;++i) if(i%p) ans=ans*i%pw; return ans*fac(x/p,p,pw)%pw; } LL C(LL x,LL y,LL p,LL pw){ if(x<y) return 0; LL f1=fac(x,p,pw),f2=fac(y,p,pw),f3=fac(x-y,p,pw); // printf("%lld %lld %lld %lld %lld ",p,pw,f1,f2,f3); int cnt=0; for(LL i=x;i;i/=p) cnt+=i/p; for(LL i=y;i;i/=p) cnt-=i/p; for(LL i=x-y;i;i/=p) cnt-=i/p; // printf("cnt:%d ans:%lld ",cnt,f1*inv(f2,pw)%pw*inv(f3,pw)%pw*mgml(p,cnt,pw)%pw); return f1*inv(f2,pw)%pw*inv(f3,pw)%pw*mgml(p,cnt,pw)%pw; } LL CHR(LL x,LL y){ // printf("CHR:%lld %lld ",x,y); LL ans=0; for(int i=1;i<=cnt;++i){ LL a,b;exgcd(P/pw[i],pw[i],a,b); // printf("C:%lld ",C(x,y,p[i],pw[i])); ans=(ans+P/pw[i]*a*C(x,y,p[i],pw[i])%P+P)%P; } return ans; } main(){ P=read(),n=read(),m=read(); for(int i=1;i<=m;++i) w[i]=read(),tmp+=w[i]; if(tmp>n) return !puts("Impossible"); int tmpp=P; cnt=0; for(LL i=2;i*i<=P;++i){ if(tmpp%i) continue; p[++cnt]=i;pw[cnt]=1; while(tmpp%i==0) c[cnt]++,pw[cnt]*=i,tmpp/=i; } if(tmpp!=1) p[++cnt]=tmpp,c[cnt]++,pw[cnt]=tmpp; LL ans=1; for(LL i=1,tmp=0;i<=m;++i){ ans=1LL*ans*CHR(n-tmp,w[i])%P; // printf("%lld %lld ",i,ans); tmp+=w[i]; } printf("%lld ",(ans%P+P)%P); } inline int read(){ register int x=0,f=1;register char ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+ch-48,ch=getchar(); return x*f; }
crt
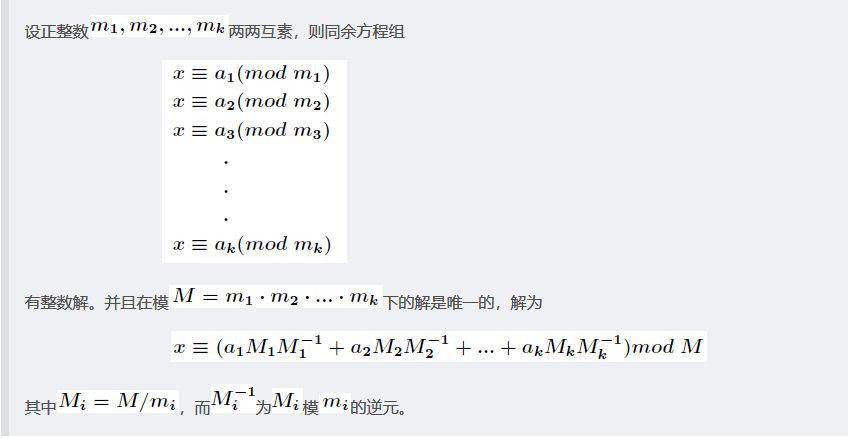
excrt
excrt和crt没有关系,这是前提。
$xequiv a_1pmod {m_1}$
$xequiv a_2pmod {m_2}$
当m1,m2互质时,就可以直接用exgcd搞一搞,答案就是lastans+a2*M/m2*a,a是exgcd中M/m2对m2的逆元。
当m1,m2不互质时,就要用excrt来搞事情。
每次考虑前i-1和i两个式子,此时的m1就是前i-1个m的lcm,此时的a1就是前i-1个式子的答案。
我们知道
x=a1+k1*m1
x=a2+k2*m2
那么a1+k1*m1=a2+k2*m2
那么k1*m1-k2*m2=a2-a1
设g=gcd(m1,m2)
那么如果(a2-a1)%g,就不存在解
否则求出一组$k1,k2$的合法解
由于x=a1+k1*m1
新的x=x(a1)+k1*m1 %lcm(m1,m2)
这样计算n-1次就得到了最终的答案。

#include<bits/stdc++.h> using namespace std; #define ll long long ll n; ll m[100005],a[100005]; void exgcd(ll a,ll b,ll &x,ll &y){ if(!b) {x=1;y=0;return;} exgcd(b,a%b,y,x); y-=(a/b)*x; } ll gcd(ll a,ll b){return b?gcd(b,a%b):a;} inline void exCHR(){ for(int i=1;i<=n;++i) scanf("%lld%lld",&m[i],&a[i]); ll A=a[1],M=m[1]; for(int i=2;i<=n;++i){ ll g=gcd(M,m[i]); if((a[i]-A)%g) return puts("-1"),void(); ll k1,k2,del=(a[i]-A)/g,m1=M,m2=m[i]; exgcd(m1,m2,k1,k2); k1=k1*del%m2; M=M/g*m[i]; A=(A+k1*m1%M+M)%M; } printf("%lld ",A); } int main(){ while(~scanf("%lld",&n)) exCHR(); return 0; }
bsgs
额先讲下bsgs吧。
bsgs解决的是$x^aequiv b (mod p)$最小的a。
p保证与x互质。
因为我们知道有$phi(p)$<=p,又有当a,p互质时$a^{phi(p)}equiv 1 (mod p)$ 费马小定理
因此最小的a一定<=p。
我们设m=$sqrt p$,那么a=cm-d,$cin [1,m],din [0,m)$
那么原式就变成了$x^{cm}equiv bx^d (mod p)$
枚举d把$bx^d$放到map里,再枚举c查表碰到有直接break即可
枚举d方便大的覆盖小的使cm-d最小。

#include<bits/stdc++.h> using namespace std; int p; map<int,int>M; int ksm(int x,int y){ int s=1; while(y){if(y&1)s=1ll*s*x%p;x=1ll*x*x%p;y>>=1;} return s; } int main(){ int x,y; cin>>p>>x>>y; int m=sqrt(p)+1; int s=y; for(int i=0;i<m;i++){ M[s]=i;//能更新就更新 s=1ll*s*x%p; } int t=ksm(x,m);s=1; for(int i=1;i<=m;i++){ s=1ll*s*t%p; if(M.count(s)){printf("%d ",i*m-M[s]);return 0;} } puts("no solution");return 0; }
exbsgs
exbsgs用于解决$x^aequiv b (mod p)$最小的a。
p不一定与x互质。
设g=gcd(p,x),若g不能整除b,那么只有b=1,a=0时有解,否则无解。
$x^{a-1}frac{x}{g}equiv frac{b}{g} mod frac{p}{g}$
直到分解到g=1为止
那么式子就变成了$x^{a-t}×frac{x^t}{prod g_i}equiv frac{b}{prod g_i} pmod {frac{p}{prod g_i}}$
然后首先检验x=[0,t)是否为解,显然t是log级别的
如果[0,t)都不是解,由于$x,frac{p}{prod d_i}$互质,BSGS求解即可
最后记得答案加上t啊
没打代码,放网上一个大佬 的

#include<bits/stdc++.h> using namespace std; int re(){ int x=0,w=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar(); return x*w; } int p; map<int,int>M; void mul(int&x,int y){x=1ll*x*y%p;} int ksm(int x,int y){ int s=1; while(y){if(y&1)mul(s,x);mul(x,x);y>>=1;} return s; } void exbsgs(int x,int y){ if(y==1){puts("0");return;} int d=__gcd(x,p),k=1,t=0; while(d^1){ if(y%d){puts("No Solution");return;} ++t;y/=d;p/=d;mul(k,x/d); if(y==k){printf("%d ",t);return;} d=__gcd(x,p); } int s=y;M.clear();int m=sqrt(p)+1; for(int i=0;i<m;i++){ M[s]=i;mul(s,x); } s=k;k=ksm(x,m); for(int i=1;i<=m;i++){ mul(s,k); if(M[s]){printf("%d ",i*m-M[s]+t);return;} } puts("No Solution"); } int main(){ int x,y; while(1){ x=re(),p=re(),y=re(); if(!x&&!p&&!y)break; x%=p;y%=p; exbsgs(x,y); } return 0; }
|
kuku kxkx |
MTT
用于解决任意模数NTT,一种简洁的方式是4次FFT得解。
A*B,把A拆成a*32768+b的形式,B同理,拆成c*32768+d。
由于卷积具有分配率
最后答案就是a*c*32768*32768+a*d*32768+b*c*32768+b*d
现在问题在如何求出这四个卷积。
令复数‘a’=(a,b),’b‘=(c,d)
变成点值式后通过把'b'reverse再把虚部取反就得到了(c,-d)的点值式
原因:把w带入为(cos,sin)
(c,d)×(cos,sin)=(ccos-dsin,csin+dcos)
把'b'reverse再把虚部取反
reverse相当于w成为共轭复数w’,就是
(c,d)×(cos,-sin)=(ccos+dsin,-csin+dcos)
再把虚部取反=(ccos+dsin,csin-dcos)
把(c,-d)带入'b'
(c,-d)*(cos,sin)=(ccos+dsin,csin-dcos)
把(c,-d)给'c'
点值式'a'*'b','a'*'c'
就得到了(ac-bd,ad+bc),(ac+bd,bc-ad)
加加减减就得到了答案。
自然数幂和是k+1次多项式原因
伯努利数
求自然数幂和,可以用伯努利数和插值计算。
B-公式
$B_0=1 sum_{i=0}^{n}B_iC_{n+1}^i=0->B_n=-frac{1}{n+1}sum_{i=0}^{n-1}B_iC_{n+1}^i$
B+把B[1]置为+1/2
用B+求自然数幂和
$sum_{i=1}^{n}i^k=frac{1}{k+1}sum_{i=0}^{k+1}C_{k+1}^iB_in^{k+1-i}$
用B-求出的是i=[0,n-1]时的答案,两种B在不同时候用效果更好
同时有组合数和某个数单独的逆元,一定记得是单独的逆元!不是阶乘
虚树
如果要统计的信息只跟数量很少的关键点相关就可以把这些关键点和lca抽出来建成一张新图。
把要建的关键点按照dfn序排序,并预处理ST表求lca,那么新加入的点和栈顶元素的lca就一定不是新加入的点。
建一个栈,站内存储一条最右边的链的信息,对于新加入的点x,设它和栈顶的元素的lca为lca。
首先如果没有栈顶元素就直接加入。
考虑lca与sta[sta[0]-1]的dfn关系,若lca比它还小(<=)那么就把栈顶和栈顶-1元素建边弹掉栈顶。
若栈顶不是lca,就把栈顶和lca建边,并把栈顶赋为lca。
最后再把x加入栈内。

struct FKT{ int B,root; int head[N],to[N<<1],nxt[N<<1],sta[N],buc[N]; ll cnt[N]; void link(int x,int y){ //printf("%d -> %d ",x,y); to[++B]=y,nxt[B]=head[x],head[x]=B; } void insert(int x){ cnt[x]=phi[x]; if(sta[0]==0) {sta[++sta[0]]=x;return;} int lca=LCA(x,sta[sta[0]]); while(sta[0]>1&&seq[sta[sta[0]-1]]>=seq[lca]) link(sta[sta[0]-1],sta[sta[0]]),sta[0]--; if(sta[sta[0]]!=lca) link(lca,sta[sta[0]]),sta[sta[0]]=lca; sta[++sta[0]]=x; } ll dfs(int x){ ll ret=0,ans=0,d=cnt[x]; for(int i=head[x];i;i=nxt[i]) ans=(ans+dfs(to[i]))%mod,ret=(ret+cnt[x]*cnt[to[i]])%mod,(cnt[x]+=cnt[to[i]])%=mod; return (ans+2ll*dep[x]*ret%mod+d*d%mod*dep[x]%mod+mod)%mod; } void clear(int x){ for(int i=head[x];i;i=nxt[i]) clear(to[i]); head[x]=cnt[x]=0; } ll Getans(int T){ ll x=0; for(int i=1;i*T<=n;++i) x=(x+phi[i*T])%mod; ll y=0; for(int i=1;i*T<=n;++i) y=(y+phi[i*T]*dep[i*T]%mod*x%mod)%mod; buc[0]=0; for(int i=1;i*T<=n;++i) buc[++buc[0]]=i*T; sort(buc+1,buc+buc[0]+1,cmp); sta[0]=0; for(int i=1;i<=buc[0];++i) insert(buc[i]); while(sta[0]>1) link(sta[sta[0]-1],sta[sta[0]]),sta[0]--; root=buc[1]; for(int i=2;i<=buc[0];++i) root=LCA(root,buc[i]); y=2ll*y%mod-2ll*dfs(root)%mod; clear(root); B=0; return (y%mod+mod)%mod; } }fkt;
线段树维护MST(最小生成树)
这款黑科技是我在看rvalue博客时看到他说自己随手切的一道题,就滚去学了。
一个2行m列的网格,求区间的最小生成树,线段树维护区间lp,rp,ans,表示区间最左端竖边,最右端,MST值。
合并左右子树先连上横着mid->mid+1的两条横边,那么这会和左右最近竖边形成环,找到环上最大值减掉更新答案。
杨氏矩阵
一种矩阵,一个点左,上要么没有点,要么有点且值比该点小。
用n个不同的数覆盖矩阵的方案数:$frac{n!}{prod H(i,j)}$
H(i,j)为钩子长.钩子长为右边和下边元素个数+1。
拉格朗日插值
- 一维拉格朗日插值
$d(x_k)=sum_{i=1}^ny_iprod_{i!=j}frac{x_k-x_j}{x_i-x_j}$
常规做法O(n^2),如果xi取值连续的话预处理阶乘逆元等可以做到O(n)
- 一维拉格朗日插系数
发现pai后面是一个多项式的形式,于是把每个多项式的系数加起来求出了系数.常规做法O(n^3)
预处理所有(x-i)的积O(n^2),然后通过长除法O(n)得到需要的多项式.可以做到O(n^2)

#include<bits/stdc++.h> #define ll long long using namespace std; const int maxn = 2e3 + 50; ll mod = 998244353; ll qm(ll a, ll b){ ll res = 1; while(b) { if(b&1)res = res*a%mod; a = a*a%mod, b>>=1; }return res; } ll a[maxn], b[maxn], c[maxn], temp[maxn]; ll x[maxn], y[maxn]; int n; void mul(ll *f, int len, ll t){//len为多项式的次数+1,函数让多项式f变成f*(x+t) for(int i = len; i > 0; --i) temp[i] = f[i], f[i] = f[i-1]; temp[0] = f[0], f[0] = 0; for(int i = 0; i <= len; ++i) f[i] = (f[i] + t*temp[i])%mod; } void dev(ll *f, ll *r, ll t){//f是被除多项式的系数,r保存f除以x+t的结果 for(int i = 0; i <= n; ++i) temp[i] = f[i]; for(int i = n; i > 0; --i){ r[i-1] = temp[i]; temp[i-1] = (temp[i-1] - t*temp[i])%mod; } return; } void lglr(){ memset(a,0,sizeof a); b[1] = 1, b[0] = -x[1]; for(int i = 2; i <= n; ++i){ mul(b, i, -x[i]); }//预处理(x-x1)*(x-x2)...*(x-xn) for(int i = 1; i <= n; ++i){ ll fz = 1; for(int j = 1; j <= n; ++j){ if(j == i) continue; fz = fz*(x[i] - x[j])%mod; } fz = qm(fz, mod-2); fz = fz*y[i]%mod;//得到多项式系数 dev(b, c, -x[i]);//得到多项式,保存在b数组 for(int j = 0; j < n; ++j) a[j] = (a[j] + fz*c[j])%mod; } } int main() { ll k; cin>>n>>k; for(int i = 1; i <= n; ++i) scanf("%lld%lld",&x[i],&y[i]); lglr(); ll ans = 0; ll res = 1; for(int i = 0; i < n; ++i){ ans = (ans + res*a[i])%mod; res = res*k%mod; } ans = (ans + mod)%mod; cout<<ans<<endl; }
- 二维拉格朗日插值
$f(x,y)=sum_{i=1}^nsum_{j=1}^mv(i,j)prod_{k!=i}frac{x-x_k}{x_i-x_k}prod_{d!=j}frac{y-y_d}{y_j-y_d}$
常规做法O(n^4),如果xi取值连续的话预处理阶乘逆元等可以做到O(n^2)
- 二维拉格朗日插系数
同一维的插系数做法。常规做法O(n^4)
同一维的插系数做法。可以做到O(n^3)
多项式长除法
对一个多项式进行除法。可以做到O(n)

但是我们一般需要的拉格朗日时用的长除法由于一定能整除,所以可以做乘法的逆运算。
K重区间覆盖问题
每个点最多被K个区间覆盖,每个询问区间有权值,求最大权值。
这个点向下个点连边流量为k费用为0,区间起点向终点连边流量为1费用为w。
这样做如果有一个点流量超过了k,其他点就不会满足条件。
只有不相交的区间才能共用一个流量,对于一个点来说每个询问区间都必定占一个流量。
三元环计数
将点按度数排序,将边重定向,方向为度数小的指向度数大的。
$deg<sqrt m$:O($msqrt m$)
$deg>sqrt m$:由于$deg>sqrt m$的点最多的有$sqrt m$种,所以最多连边O($msqrt m$)
四元环计数

inline bool cmp(const int& _this,const int& _that) {return d[_this]<d[_that]||(d[_this]==d[_that]&&_this<_that);} #define con const int& inline void main() { n=g(),m=g(); for(R i=1,u,v;i<=m;++i) u=g(),v=g(),e[u].push_back(v),e[v].push_back(u); for(R i=1;i<=n;++i) d[id[i]=i]=e[i].size(); sort(id+1,id+n+1,cmp); for(R i=1;i<=n;++i) rk[id[i]]=i; for(R u=1;u<=n;++u) for(con v:e[u]) if(rk[v]>rk[u]) f[u].push_back(v); for(R u=1;u<=n;++u) { for(con v:e[u]) for(con w:f[v]) if(rk[w]>rk[u]) ans+=c[w],++c[w]; //交换e与f的枚举顺序也是对的。 for(con v:e[u]) for(con w:f[v]) if(rk[w]>rk[u]) c[w]=0; //清空桶。 } printf("%lld ",ans); }
View Code
括号匹配
左括号序列合法的条件
前缀和大于等于0或当前后缀和大于等于最大后缀和
右括号序列合法的条件
后缀和小于等于0或当前前缀和小于等于最小前缀和
快速乘
inline ll ksc(ll x,ll y) { return (x*y-(ll)((long double)x/mod*y)*mod+mod)%mod; }
例题:模拟58 T1
LGV定理(多条路径不相交方案数)

计算$(1,1)$到$(n,m)$的两条路径不交的方案数.
先考虑计算$(1,2)$到$(n-1,m)$和$(2,1)$到$(n,m-1)$的方案
那么不合法的情况就是有偶数个交点的情况

如果交换终点就会变成有奇的个交点的相交路径
并且这些相交路径覆盖了所有的情况(因为交换了终点必然相交,而观察发现又必然是奇个交点)
因此,最终的答案就是$ans[(1,2)->(n-1,m)]*ans[(2,1)->(n,m-1)]-ans[(1,2)*(n,m-1)]*ans[(2,1)*(n-1,m)]$
例题:模拟58 T2
动态dp
带修改求最大独立集
暴力做法就是每次都树形$dp$求,复杂度$O(qn)$
发现如果只有一条链就可以矩阵乘法优化
考虑设出来的$dp$状态变成了除了某个子树,这样就可以用重链剖分优化重链复杂度了,线段树维护矩阵然后求出来重链顶端的真实$dp$值然后给父亲转移,轻链直接暴力转移了
可并堆
可并堆,又称为左偏树,满足从一个节点一直向左儿子走比一直向右儿子走距离更长。
这样,它就满足了往右走最多log次,也就是每次合并的时间复杂度为O(log)
合并:将一个合并到另一个的右儿子上,合并的同时满足堆的所有性质。

#include<cstdio> #include<algorithm> #define rep(i, a, b) for (register int i=(a); i<=(b); ++i) #define per(i, a, b) for (register int i=(a); i>=(b); --i) using namespace std; const int N=100005; int rt[N], ls[N], rs[N], val[N], dis[N]; inline int read() { int x=0,f=1;char ch=getchar(); for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1; for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0'; return x*f; } int find(int x){return x==rt[x]?x:rt[x]=find(rt[x]);} int Merge(int x, int y) { if (!x || !y) return x|y; if (val[x]>val[y] || (val[x]==val[y] && x>y)) swap(x, y); rs[x]=Merge(rs[x], y); if (dis[ls[x]]<dis[rs[x]]) swap(ls[x], rs[x]); rt[x]=rt[ls[x]]=rt[rs[x]]=x; dis[x]=dis[rs[x]]+1; return x; } int Delete(int x) { val[x]=-1; rt[ls[x]]=ls[x]; rt[rs[x]]=rs[x]; rt[x]=Merge(ls[x], rs[x]); } int main() { int n=read(), m=read(); dis[0]=-1; rep(i, 1, n) rt[i]=i, val[i]=read(); rep(i, 1, m) { int opt=read(), x=read(); if (opt==1) { int y=read(); if ((!~val[x]) || (!~val[y])) continue; int fx=find(x), fy=find(y); if (fx^fy) rt[fx]=rt[fy]=Merge(fx, fy); } else { if (!~val[x]) puts("-1"); else printf("%d ", val[find(x)]), Delete(find(x)); } } return 0; }
二次剩余
已知$n$,用来求解$x^2=n(mod p)$的$x$
几个相关必背的性质

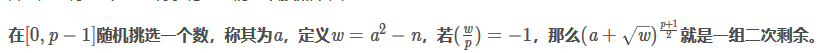
最后一句的实现我并不明白,但是可以看代码

struct field{ int x,y; field(int a=0,int b=0){ x=a;y=b; } }; field operator*(field a,field b){return field(a.x*b.x%p+a.y*b.y%p*w%p,a.x*b.y%p+a.y*b.x%p);} int ran(){ static int seed=23333; return seed=((((((ll)seed^20030927)%p+330802)%p*9410)%p-19750115+p)%p^730903)%p; } int pows(int a,int b){ int base=1; while(b){ if(b&1) base=base*a%p; a=a*a%p;b/=2; } return base; } field powfield(field a,int b){ field base=field(1,0); while(b){ if(b&1) base=base*a; a=a*a;b/=2; } return base; } int legander(int x){ int a=pows(x,(p-1)/2); if(a+1==p) return -1; return a; } int surplus(int x){ int a; if(legander(x)==-1) return 0; while(1){ a=ran()%p; w=((a*a-x)%p+p)%p; if(legander(w)==-1) break; } field b=field(a,1); b=powfield(b,(p+1)/2); return b.x; }
Miller_Rabin
作用:判断素数

#include<cstdio> #include<ctime> #include<cstdlib> #define ll long long using namespace std; ll mod,p[9]={2,3,5,7,11,13,17,19,23}; ll mo(ll a){return a>=mod?a-mod:a;} ll ksc(ll a,ll b){return ((a*b-(ll)((long double)a*b/mod)*mod)%mod+mod)%mod;} ll mgml(ll a,ll b,ll ans=1){ for(;b;b>>=1,a=ksc(a,a)) if(b&1) ans=ksc(ans,a); return ans; } bool Miller_Rabin(ll n){ mod=n; for(int i=0;i<=8;++i){ if(p[i]==n) return 1; else if(p[i]>n) return 0; ll tmp=mgml(p[i],n-1),tnp=n-1; if(tmp!=1) return 0; while(tmp==1&&tnp%2==0){ tnp/=2; tmp=mgml(p[i],tnp); if(tmp!=1&&tmp!=n-1) return 0; } } return 1; } int main(){ ll n; while(scanf("%lld",&n)!=EOF) puts(Miller_Rabin(n)?"Y":"N"); return 0; }
拉普拉斯定理
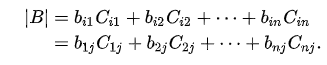
$|B|$:行列式的值,$b$:行列式,$c$:代数余子式(代数余子式:$c_{i,j}$表示$(-1)^{i+j}*$去掉$i$行$j$列后余子式的值
伴随矩阵
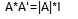
$A$:行列式
$A'$:伴随矩阵
$|A|$:行列式的值
$I$:单位矩阵
伴随矩阵是代数余子式的转置
...
