题目
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
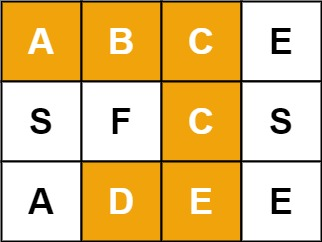
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
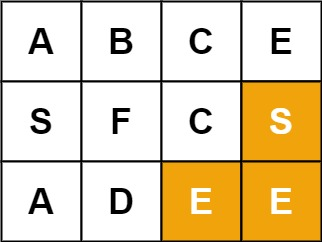
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出:true
示例 3:

输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出:false
提示:
m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/word-search
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题方法
DFS回溯
1.双重循环找到字符串的起点
2.基于起点上下左右四个方向找剩余路径
3.在找的过程中判断选择是否正确,是否越界,是否已访问过
4.声明一个变量保存访问过的元素
5.如果递归下一个节点时错误的,说明当前选择也是错误的,需要把当前元素的是否访问状态改回未访问
时间复杂度O(MN*3^L) M,N为网格的长宽 L为字符串长度 每次递归除了第一次可以进入4个分支,
其余最多进入3个分支,因为每个位置只能一次,走过无法再访问。
空间复杂度O(MN) 开辟存储是否访问过的数组
如果采用修改原数组的方法 空间复杂度O(1)
代码
// dfs + 辅助数组
func exist(board [][]byte, word string) bool {
m,n := len(board),len(board[0])
// 访问记录
visited := make([][]bool,m)
for i := 0;i < m;i++{
visited[i] = make([]bool,n)
}
var canFind func(r,c,i int) bool
canFind = func(r, c, i int) bool {
// 已经找到复合字符串长度的路径
if i == len(word){
return true
}
// 索引越界
if r < 0 || r >= m || c < 0 || c >= n{
return false
}
// 当前元素已访问过或者当前元素不等于当前需要找的字符
if visited[r][c] || board[r][c] != word[i] {
return false
}
// 设置当前元素为已访问状态
visited[r][c] = true
// 递归剩余路径 在 || 判断中,只要有符合的便不会继续执行后面的判断,达到剪枝的目的
if canFind(r+1,c,i+1) || canFind(r-1,c,i+1) || canFind(r,c+1,i+1) || canFind(r,c-1,i+1){
return true
}
// 没有符合的路径 将当前元素访问状态回退
visited[r][c] = false
return false
}
for i := 0;i < m;i++ {
for j := 0;j < n;j++{
if board[i][j] == word[0] && canFind(i,j,0){
return true
}
}
}
return false
}
// dfs + 直接修改原数组
func exist2(board [][]byte, word string) bool {
m,n := len(board),len(board[0])
var canFind func(r,c,i int) bool
canFind = func(r, c, i int) bool {
// 已经找到复合字符串长度的路径
if i == len(word){
return true
}
// 索引越界
if r < 0 || r >= m || c < 0 || c >= n{
return false
}
// 如果当前元素不等于寻找元素
if board[r][c] != word[i] {
return false
}
// 修改元素,表示已访问
temp := board[r][c]
board[r][c] = ' '
// 递归剩余路径 在 || 判断中,只要有符合的便不会继续执行后面的判断,达到剪枝的目的
if canFind(r+1,c,i+1) || canFind(r-1,c,i+1) || canFind(r,c+1,i+1) || canFind(r,c-1,i+1){
return true
}
// 没有符合的路径 将当前元素回退
board[r][c] = temp
return false
}
for i := 0;i < m;i++ {
for j := 0;j < n;j++{
if board[i][j] == word[0] && canFind(i,j,0){
return true
}
}
}
return false
}