1.引言
2.位运算基础
3.位运算在角色权限设计中的应用
4.为什么in32的范围是-2^31 ~ 2^31-1 ?
5.同余的概念
6.模的概念帮助理解补数和补码。
一、引言
这周在做一个新增角色权限需求时,遇到下面这样一行代码,这篇文章将围绕这行代码展开。
user.RoleType = ~(~user.RoleType | 511) | requestDTO.Role;
二、位运算基础
关于位运算的基础知识参见:
百度百科:https://baike.baidu.com/item/%E4%BD%8D%E8%BF%90%E7%AE%97
维基百科:https://zh.wikipedia.org/wiki/%E4%BD%8D%E6%93%8D%E4%BD%9C
总结如下:
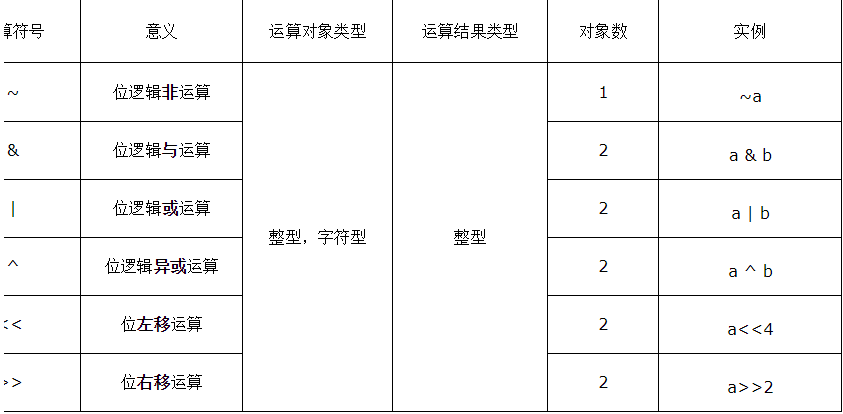
三、位运算在角色权限设计中的应用(优缺点)
业务场景:有A.B.C.D四个基础角色,现在需要新增一个复合角色(架构师),可以配置用户。
下面是一个demo例子,位运算在角色权限中的应用
[Flags]
public enum RoleType
{
/// <summary>
/// 无角色
/// </summary>
[Description("无角色")]
None = 0,
/// <summary>
/// 普通用户角色
/// </summary>
[Description("普通用户")]
A = 1,
/// <summary>
/// 初级开发
/// </summary>
[Description("初级开发")]
B = 2,
/// <summary>
/// 中级开发
/// </summary>
[Description("中级开发")]
C = 4,
/// <summary>
/// 高级开发
/// </summary>
[Description("高级开发")]
D = 8,
/// <summary>
/// 架构师
/// </summary>
[Description("架构师")]
E = 16 //纠正原文错误
}
public class UnitTest1
{
public static void Test1()
{
var a = RoleType.A | RoleType.B; //变量a为 A | B
var b = RoleType.B | RoleType.D; //变量b为 B | D
var aa = a.ToString();//变量aa为 "A,B"
var bb = a & (~RoleType.A);//从组合状态中去掉一个元素A ,结果为 枚举 B
var bb1 = ~(~a | RoleType.A); //bb结果等价于bb1
var cc = (b & RoleType.B) != 0;//检查组合状态是否包含枚举 B
var dd = RoleType.A | RoleType.B | RoleType.B | RoleType.B; //变量dd为 A | B
}
}
分析:
1.为什么枚举角色数都是2的倍数?
十进制 二进制
1 01
2 10
4 100
8 1000
。。。。。。
我们发现在各个位上值都是唯一的,所以做位或运算时,不同值的运算结果是唯一的;反过来,我们也可以根据结果值推算出来包含的枚举(即业务中的角色)
ok,到这里我们再看开头引言中的那行代码,可以写为
user.RoleType = (user.RoleType & ~511) | requestDTO.Role;
抽象为x=(x&~y)|z,就是去除x中的y角色,再与z做位或组合。
想下,这个在保存用户角色的时候会很巧妙,就是去除用户 x(原有角色)中的 y(基础角色),再和z(要保存的角色),做位或运算组合 得出一个新的要保存角色。
优点:一个roletype字段可以保存用户的所有角色信息
缺点:当已经有31个角色,当需要再新增角色的时候,就变的尴尬了(超出了int32位)
解决办法:
1.将roletype字段扩展为64位,但在系统的后期迭代阶段影响范围颇大,还是存在用完的时候
2.新增一张表,将复合角色与基础角色 这两个拆分位两个字段,单独保存两者之间关系
四、为什么in32的范围是-2^31 ~ 2^31-1 ?
为什么会介绍这个问题,因为当新增角色时,2^32超出了int32的范围,但是为什么int32范围是-2^31 ~ 2^31-1 ?本着对刨根问底的态度,便追寻了下去。
我们可以先研究下8位二进制的标识范围为什么是-2^7~2^7-1
这里要说下 原码,反码,补码的概念。
原码
正数的原码就是它的本身
假设使用一个字节存储整数,整数10的原码是:0000 1010
负数用最高位是1表示负数
假设使用一个字节存储整数,整数-10的原码是:1000 1010
反码
正数的反码跟原码一样
假设使用一个字节存储整数,整数10的反码是:0000 1010
负数的反码是负数的原码按位取反(0变1,1变0),符号位(首位)不变
假设使用一个字节存储整数,整数-10的反码是:1111 0101
补码
正数的补码和原码一样
假设使用一个字节存储整数,整数10的补码是:0000 1010(这一串是10这个整数在计算机中存储形式)
负数的补码是负数的反码加1
假设使用一个字节存储整数,整数-10的补码是:1111 0110(这一串是-10这个整数在计算机中存储形式)
在计算机中,为什么不用原码和反码,而是用补码呢?
使用原码计算10-10
0000 1010 (10的原码)
+ 1000 1010 (-10的原码)
------------------------------------------------------------
1001 0100 (结果为:-20,很显然按照原码计算答案是否定的。)
分析:正常的加法规则不适用于正数与负数的加法,因此必须制定两套运算规则,一套用于正数加正数,还有一套用于正数加负数。从电路上说,就是必须为加法运算做两种电路
使用反码计算10-10
0000 1010 (10的反码)
+ 1111 0101 (-10的反码)
------------------------------------------------------------
1111 1111 (计算的结果为反码,我们转换为原码的结果为:1000 0000,最终的结果为:-0,很显然按照反码计算答案也是否定的。)
使用补码计算10-10
0000 1010 (10的补码)
+ 1111 0110 (-10的补码)
------------------------------------------------------------
1 0000 0000 (由于我们这里使用了的1个字节存储,因此只能存储8位,最高位(第九位)那个1没有地方存,就被丢弃了。因此,结果为:0)
分析:补码表示法可以将加法运算规则,扩展到整个整数集,从而用一套电路就可以实现全部整数的加法。补码是计算机中存储整数的形式。
八位二进制正数的补码范围是0000 0000 ~ 0111 1111 即0 ~ 127
负数的补码范围是正数的原码0000 0000 ~ 0111 1111 取反加一(也可以理解为负数1000 0000 ~ 1111 1111化为反码末尾再加一)。 所以得到 1 0000 0000 ~ 1000 0001
1000 0001作为补码,其反码是1000 0000,其原码是1111 1111(-127)
依次往前推,可得到1111 1111作为补码,其反码1111 1110,原码1000 0001(-1)
那么补码0000 0000(1被舍去)的原码是1000 0000符号位同时也可以看做数字位即表示-128(-2^7)
类推:in32的范围便是-2^31 ~ 2^31-1
五、同余的概念
两个整数a,b,若它们除以整数m所得的余数相等,则称a,b对于模m同余
记作 a ≡ b (mod m)
读作 a 与 b 关于模 m 同余。
六、模的概念
时间不早了,模的概念可以帮助理解补数和补码,下篇博客中提到吧。。。
原文地址:https://www.cnblogs.com/jdzhang/p/9034171.html
