树

树——普遍存在的层次管理

为什么要用树

分层次组织在数据管理上有更高的效率

数据管理的基本操作之一：查找

如何实现有效率的查找？

查找分两种

静态查找：集合中记录是固定的，没有插入和删除操作，只有查找

动态查找：集合中记录是动态变化的，出了查找还有插入和删除

对于静态查找，如果采用顺序查找的方式，那么就是遍历整个集合，时间复杂度是O(N)，效率很低

二分查找

二分查找具有对数的时间复杂度O(logN)

为什么二分查找的效率高呢？

因为数据事先做好了有序化的处理

判定树

• 判定树上的每个结点需要查找的次数刚好为该结点的层数
• 查找成功的次数不会超过该树的深度

• n 个结点的判定树的深度为[log₂n]+1   ([]表取整，小于该数的最大整数）

综上，也就是说最坏查找次数为[log₂n]+1

如果以查找树的形式来存储数据，查找效率能达到跟二分查找差不多的效果，最大的优点是，当在树里面插入删除结点比在数组里面方便得多，所以，用这种方式可以很好得解决动态查找的问题！

树的定义

n（n≥0）个结点构成的有限集合

当n=0 时，称为空树

树的实现

数组？以一定顺序存储在里面，但是很难知道每一个结点的父节点或者子节点

链表加结构来实现？

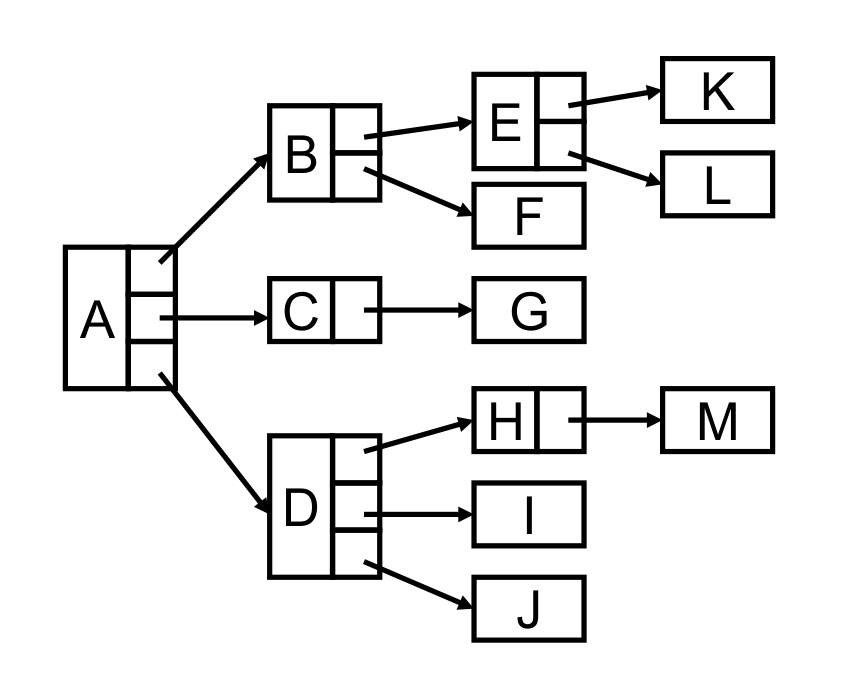
好像实现了树，但是每个结点的结构是不同的，无法知道一个结点到底有多少个儿子，给程序实现造成困难。

那每个结点都用一样的结构？因为每个结点的儿子数都不同的话，会造成空间浪费！

儿子兄弟法

 每个结点都是同样的结构，两个指针域分别指向该结点的儿子和兄弟

如果n个结点，那么就有2n个指针域，有n-1条边，那么意味着有n-1个指针域是非空的，浪费的空间为n+1

把那棵树旋转45度，就得到传说中的二叉树，二叉树是在树结构研究里面最重要最主要的内容

二叉树

一个又穷的结点集合，这个集合可以为空

满二叉树：完美二叉树， 每个结点都有两个儿子，出了最底下那一层之外

完全二叉树：从上到下，从左到右依次排下来，也就是说允许一颗满二叉树拿到后面几个元素

几个性质

• 第i层最多有2^i-1个结点（根结点为第1层）
• 深度为k的二叉树最大结点数：2^k-1（等比数列求和啊就是），一个结点深度就是1。满二叉树达到最大结点数
• 对任何非空的二叉树T，若n0表示叶子结点的个数，n2表示度为2的结点的个数，则有n2+1=n0

证明：从边的角度来看问题，首先从树的上面往下看，边的条数为S1=0*n0+1*n1+2*n2，从下往上看，每一个结点都对应一条边，除了根结点外，所以S2 = n0+n1+n2-1，S1=S2，得出n2+1=n0

 操作集

二叉树的主要操作有：

• 判别树是否为空isEmpty() 
• 遍历，按某个顺序访问每个结点
• 创建一颗二叉树

这里面又以树的遍历最为重要，因为很多算法都是建立在树的遍历的基础上的，树的遍历本质就是二维结构的一维线性化

遍历的方式

• 先序：根，左，右
• 中序：左，根，右
• 后序：左，右，根
• 层序：从上到下，从左到右

存储结构

1.顺序存储（数组）

　　上面提到用数组存储树不太方便，但是有一种树例外，那就是完全二叉树，从上到下，从左到右编号存储就可以，编号当左数组下标即可。

　　那么如何取出数据呢？有如下性质：

　　1.非根结点 i 的父节点的编号为[i / 2] ， []是取整的意思

　　2.结点 i 的左孩子序号为 2i （2i <= n , 否则没有左孩子)

　　3.结点 i 的右孩子序号为 2i + 1 （2i + 1 < n , 否则没有右孩子）

一般二叉树也可以用这种方式来存储，将空位用空元素全部补齐即可，但是当缺的结点比较多的时候这样会造成大量的空间浪费

2.链表

结点的结构设计如下：

　　

可以得到如下二叉树

树的应用

二分查找之所以快是因为实现把数据进行了有序化的存储，判定树把一个线性的查找过程变成了在树上查找，所以查找效率就是树的高度，那有没有可能直接把元素放到树上，这就是二叉搜索树，或者叫二叉查找树

二叉搜索树

左边的比根结点小，右边的比根结点大

主要操作：

　　1.find，查找某个指定元素

　　2.findMax，查找最大的元素

　　3.findMin，查找最小的元素

　　4.insert

　　5.delete

1.find

public class BinarySearch {

    public static int[] a;
    
    public BinarySearch(int[] a){
        this.a = a;
    }
    
    public static void main(String[] args){
        a = new  int[]{0 , 1 , 3 , 4 , 8 , 9 , 10 , 11 , 12 , 32 , 33 , 89 , 100 };
        int key = 99;
        int i = rank (key , 0 , a.length-1);
        if ( i < a.length && a[i] == key)
            System.out.println("length = " + a.length + " i = " + i);
        else 
            System.out.println("not found~");
        
    }
    
    public static int rank (int key , int lo , int hi){
        if ( hi < lo) return lo;
        int mid = lo + (hi - lo)/2;
        if (key < a[mid]) 
            return rank ( key , lo , mid-1);
        else if ( key > a[mid])
            return rank ( key , mid+1 , hi);
        else 
            return mid;
    }
}

not found~