堆排序

转载自：http://blog.csdn.net/caimo/article/details/7783970

堆

堆是一个完全二叉树的数组对象。树每一层都是满的，最后一层可能除外（从一个节点的左子树开始填）。

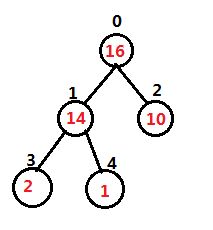
给定节点 i ，可以很容易计算父节点和子节点的位置。

Parent(i) =floor(i/2)   ：i/2再向下取整

LeftChild(i) =2*(i+1)-1   :因为i从0开始，这和c语言的数组从0开始相对应。可以用左移运算代替*，即LeftChild(i)=(i+1)<<1 - 1;

RightChild(i) = 2*(i+1)   :RightChild(i) = (i+1)<<1；

堆排序

堆排序的时间复杂度是O（nlgn），是比较有效率的一种。其使用的是最大堆。最大堆的意思是父节点的值>=孩子的值。那么第0个节点必定是该堆的最大值。所以，堆排序的思想就是每次循环把最大值移走，然后从剩下的节点重新建立最大堆。

第一步：建立堆的结构体。

typedef struct heap_t{
    int *arr;          //point for an array to store heap value.
    int heapMaxIndex;   //heap element max index number
    int arrLength;  //array length of arr

}Heap;

其中arr指针指向的是存放堆数据的数组。

heapMaxIndex是数组最大的序号。如数组定义为a[10]，那么heapMaxIndex的值应该为9.

第二步：保持堆的性质。

这一步是堆排序的基础。这里将功能写成一个函数名为void maxHeapify(Heap *hp, unsigned int nodei)，这个函数用于让一个数组变成一个符合堆性质的数组。时间复杂度为O(h)，h是堆所属二叉树树的高度=lgn(n是节点个数)。

思想是：从一个节点i，和他的孩子leftchild(i)，rightChild(i)中找到最大的，然后其索引存放在largest中。如果i是最大的。那么i为根的子树已经是最大堆，程序结束。

否则i的某个子节点有最大元素，那么i的值和largest的值交换。下标为largest的节点在交换后作为父节点，那么他可能又违反堆性质，因此递归调用该函数。

 

void maxHeapify(Heap *hp, unsigned int nodei)
{
    unsigned int l = (nodei+1) << 1 - 1;  //left child = 2i-1, -1 ?:arr[0..n-1]
    unsigned int r = (nodei+1) << 1 ; // right child = 2i
    unsigned int largest = 0;
    int heapMaxI = hp->heapMaxIndex;

    if(l <= heapMaxI && hp->arr[l] > hp->arr[nodei])
        largest = l ;
    else
        largest = nodei ;

    if(r <= heapMaxI && hp->arr[r] > hp->arr[largest])
        largest = r ;

    if(largest!=nodei)
    {
        //exchange
        int tmp ;
        tmp = hp->arr[largest];
        hp->arr[largest] = hp->arr[nodei];
        hp->arr[nodei] = tmp;

        maxHeapify(hp,largest);
    }else{
        return ;
    }

}