逆向课程第五讲逆向中的优化方式,除法原理,以及除法优化下
一丶除法的优化
1.有符号被除数 / 无符号除数的情况下
高级代码为:
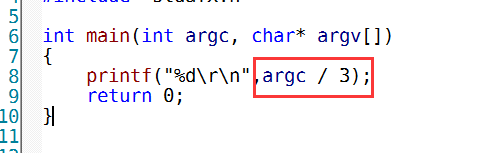
汇编中优化的体现形式

相比于昨天,我们发现了的 无符号 / 常量多出了点东西
无符号/常量

如果无符号/常量,那么我们还原的时候
套用公式即可
am >> n
a是被除数 m是设 2n/c 等价于 m == 2n/c
无符号的情况的,n的值是2^33次方 ,n = 33
根据上面得知, m = 0AAAAAAABh
此时求出C来即可, C = 除数
公式:
2n / m = c
套进去得到
2^33次方 / 0AAAAAAABh = 被除数 结果向上取整

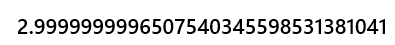
向上取整,结果就是3,那么得出被除数是3了.
2^33次方,也就是n怎么得出来的,依据上面的汇编代码n值等于1
也就是shr edx,1 那么我们知道,算一个除法的时候,必须扩展符号位
也就是 变成了 EDX.EAX 了,现在EDX右移一位,那么相当于 eax移动了32位+1,也就是33位,所以可以直接省略了.
所以此时EDX >> 1则是 33
此时继续,有符号 / 常量

看汇编代码,下边多了几条语句 显然与上面不同
此时还原的方法
n得出结果就是32,为什么?
因为edx直接使用了,我不用移位了.
下方的移动31位,是固定的,这个主要是解决有符号和无符号相除.
在这里,需要进行大量的数学公式推算,鉴于大家对数学不太明白,所以不再讲解.
我们只需要知道,当一个有符号 / 一个常量的时候,那么下方如果调整了.不用看.因为m的值如果按照 imul来计算的时候是一个负数.但是此时我们不能让它变为负数,所以最后进行符号位调整.
还原手法同上.
如果数学公式推导:
我们知道.
a/c的结果可以变为
m = 2n / c
此时我们要知道,C的结果不会是整数的,所以使用的公式 是上整+1
也可能是小数,也需要上整+1
那么现在我们可以把符号位提取出来,这样也就是 移动31位(所以说是在32位系统下是固定死的),这样如果是负数,那么负数+1即可.如果是正数,那么是加0,还原的时候只看上三句即可.
2.无符号 / 7 和有符号/7的新的优化方式(当然可能不光是7介绍的是这种优化方式)
无符号/7的新方式.

又晕了是不是,一个DIV没用到,很难看到这是一个除法对不对.
先说下还原的公式,以及方法(至于公式怎么的出来的,那么可以看下方推导,当然这属于大数问题,可以不看.不过看了有好处)
2n / (M + 2^32) = C(除数)即可.(别忘了结果向上取整)
n = 32(本身32起步,看系统,当然n的取值明天会讲) + 1 + 2 (指数相加) 结果为2 ^ 35次方
那么 2^35次方 / (M + 2^32) 结果救赎除数
那么我们按照数学界的公式去推一下.
推导:
首先得出:
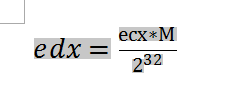
得出最后的公式.
那么根据上面的程式,继而得到了
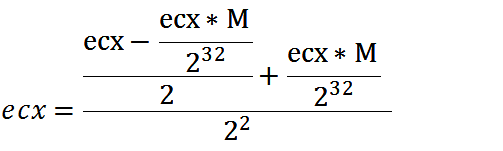
一步一步简化
第一次简化: 可以把2^32次方拿到上面来
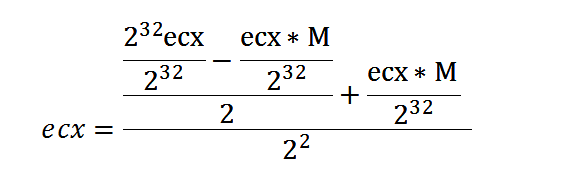
第二次简化
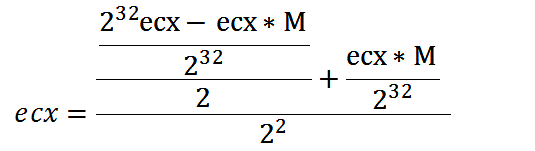
第三次简化:
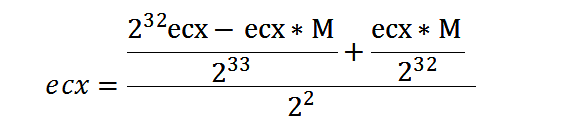
第四次简化
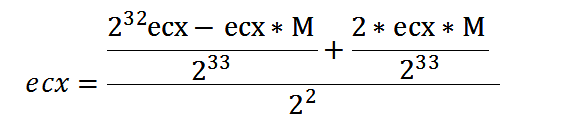
第五次简化
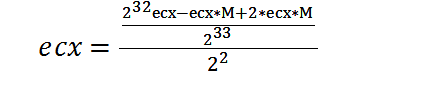
第六次简化:
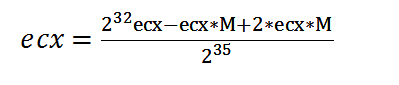
第八次简化:
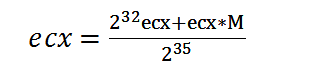
得出了
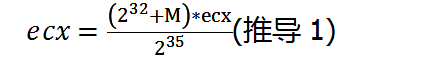
那么根据以前的除法公式
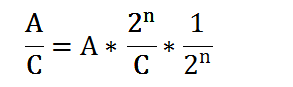
设 m = 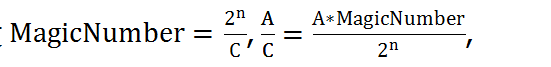
那么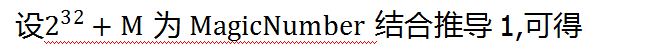

进而简化为公式得出 一个大的M, M的值太大了.变为了一个大数问题,所以我们最终的M要加上1,或者加上2^32次方.(因为进位了)
那么
C = (2^32 + 指数 + 指数) / (2^32 + M) 故而得出了C
简化为了
C = 2^n / M (别忘了M是一个大数)
有符号/7
这个和昨天一样,套用 C = 2^n / M 即可 (M是正常的,不是大数)
在这里讲解一下汇编代码:

请问为什么要 add一下.
这里我们就涉及到了有符号和无符号混乘的问题.
比如16位的年代,两个寄存器相乘,怎么解决溢出问题了.
A * 8086
A + ~A = FFFF
A + ~A + 1 = 10000 (求补码)
A * -(10000h - 8086h)
去掉负号
A * (8086h - 10000h )
那么得出
8086h - 10000h = dx.ax
又因为你减掉了补码 10000h
那么
dx.ax + 10000h = 8086h
那么此时 10000h的高位变成了1,那么 dx直接加1即可了.
所以这就是为什么 add edx,ecx(乘积的高位)
到此,除数为正数的几种情况讲解完毕.
二丶除数为负数
1.除数为 -2的幂的情况下
高级代码:
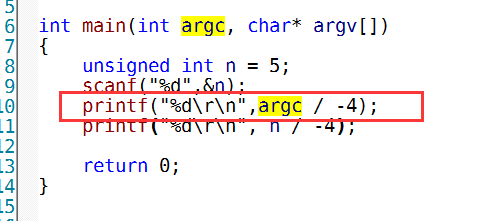
汇编代码:

公式还是一样的,向上取整的公式.也就是昨天的
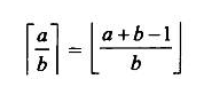
b- 1是3
b是除数, 结果是2 ^2次方.
得出除数是4 只需要求反即可.
2.除数为-7的时候,有符号除,和无符号除的表现形式
2.1 有符号除
高级代码还是上面的,只不过 -4 变为-7
argc / -7

此时,和 有符号 * 无符号问题又冲突了
A * 8086
只不过,现在的M变为负数了 需要你求补码了. 而又因为M是一个大数,下面需要调整1F(31)位,所以
还原公式为
2^n / neg(2^32 + M) = C (向上取整)
也就是说依照上图,我们的M变为了16DB6DB6D了,此时要对它取反+1变为真正的M 然后用2^n次方去除,然后求出C来(除数)
计算一下得到
2^34 / neg(16DB6DB6D) = 6.99999xxxx 向上取整是7
那么此时怎么判断是否是 ±7那?
可以看汇编代码,里面有个 sub edx,ecx(相当于上面举例子 A * 8086, 那么此时 EDX只能减去乘积的高位才会得出真正的8086)
那么此时,我们判定了m的高位是负数,是求补后的,那么得出了 M是负数,说明了除数为负数,又因为还原了,M 得出的结果是原除数的绝对值.所以判定为负数.
2.2无符号/-7的优化.

这个是特殊还原公式
还原公式:
C = 2^n / M 转为16进制当做有符号解释即可.
现在的n是29 加上原来的32 = 61 那么就是2^61次方 / 20000001h 结果转化为16进制当做有符号解释.