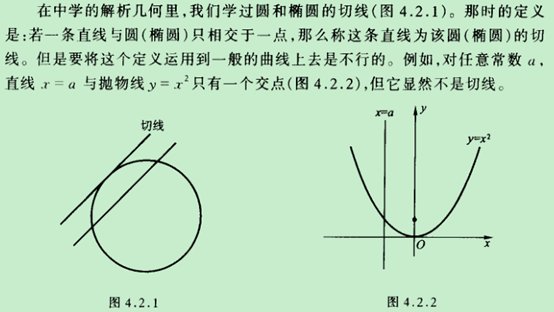
那么一般的曲线的切线该怎么定义呢?且看下文!
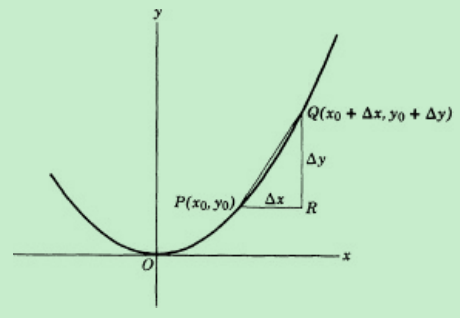
(P(x_{0},y_{0}))和(Q(x_{0} + Delta x,y_{0} + Delta y))分别是上图曲线上不同的两点(这意味着(Delta x
eq 0)),Q可以选在P的右边也可以选在左边(这意味着( ext{Δx})可正可负),称通过PQ的直线为该曲线的一条割线。在( ext{Δx})不断逼近于0的过程中,点(Q)不断逼近于P,

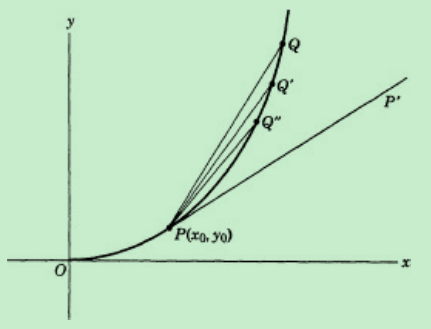
来看这个过程中的产生的割线( ext{PQ})、(PQ^{'})、( ext{PQ}^{''})…,它们不断逼近一条过点P并且刚刚(不是“仅仅”)接触点P的直线(the line through P which “just touches”the curve at P)——图中的(PP^{'})这条直线,(PP^{'})就叫作曲线在点P处的切线(割线的极限位置就叫作切线),这些割线的斜率(frac{Delta_{y}}{ ext{Δx}})逼近的就是切线(PP^{'})的斜率,如果该函数在P处有导数(f^{'}left( x_{0}
ight) = lim _{Delta x
ightarrow 0}dfrac {Delta y}{Delta x}),那么显然(f^{'}left( x_{0}
ight))也是切线的斜率[1]。
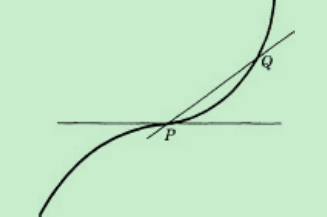
必须明确指出的是点(mathbf{Q})必须分别从左右两边逼近于点P并且过程中的产生的割线(mathbf{ ext{PQ}})、(mathbf{P}mathbf{Q}^{mathbf{'}})、(mathbf{ ext{PQ}}^{mathbf{''}})…都要逼近于同样的极限位置才能说曲线在P点有切线[2]。如何判断Q分别从两边向P逼近时产生的割线的极限位置是否相同呢?当然不能凭眼睛看一看就说位置相同,我们可以先计算Q从左边向P逼近时产生的割线的斜率的极限,然后再对比Q从右边向P逼近时产生的割线的斜率的极限,若二者相等,那么就可以断定Q分别从两边向P逼近时产生的割线的极限位置相同。通过这个判定条件我们可以知道一些有尖角的曲线在尖角处没有切线,比如y=|x|在(0,0)处就没有切线(左边的割线斜率极限是-1,右边的是1,二者不等),下图的曲线在P处(尖角)也同样没有切线。
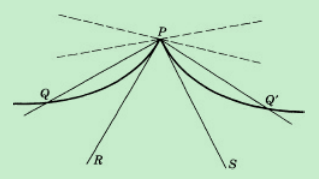
一个函数如果在某点具有导数(要求左导数等于右导数),那么其图像在该点必然也具备上述切线存在的要求,所以函数在某点有导数预示着其图像在该处有切线,反之则不然,比如对于(y = x^{frac{1}{3}})的图像,
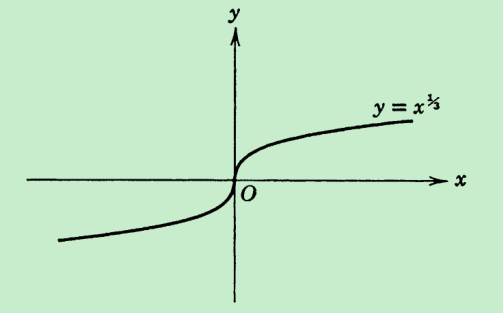
其在x=0处并无导数(我们要求导数值必须是实数,但此处非也,所以“无导数”),但是函数图像在x=0处的切线就是纵轴x=0,可以通过将函数图像旋转90°后用本文中切线定义的方法证明之,所以函数在某点无导数并不能说明其图像在该处无切线。
现在我们对比一下本文中切线的定义和文章开头提到的圆或椭圆的切线定义——不难发现,本文中切线的定义除了适用于给圆或椭圆定义切线外,还适用于给很多别的曲线定义切线,也就是说本文中切线的定义具有更广泛的意义,在接受了这个更广义的切线定义后我们便不再拘泥于中学时期的切线定义,下面两图中的水平直线均为曲线在P点处的切线,并且切线和曲线不再只有一个交点,另外图中的切线也穿过了曲线,有些书上介绍初等的切线定义时要求切线不能穿过曲线,但在广义切线定义中便再无此要求[3]。

为什么要研究切线呢?促使数学家们研究这个问题的原因之一是始于十六世纪的最优化问题,比如在几何、机械和光学领域求最大值或最小值的问题[4],解决起来要用到切线,下面举一列作简要介绍。在一个函数图像上,极大值对应着一个代表峰顶的点并且它比周围的其它点都高,极小值对应着一个代表谷底的点并且比它周围的其它点都低。在下图中,B就是一个极大值点,C是一个极小值点,
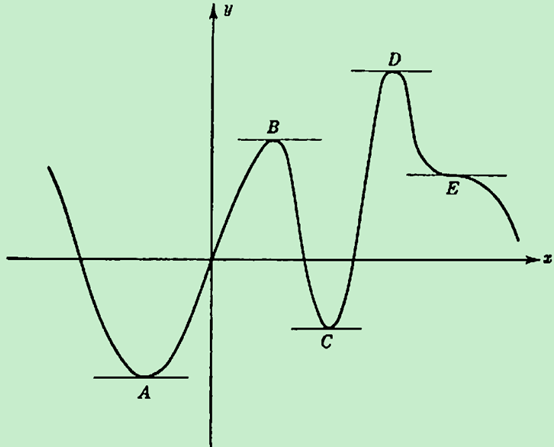
为了用统一的方式刻画极大值和极小值的这种性质,我们可以从图像上发现在极大值和极小值点处的切线都平行于x轴[5](可以严格证明该结论[6]),此时切线斜率均为0,也就是说我们可以通过解方程(f^{'}left( x
ight) = 0)的方式来找出极大值和极小值点,这就是切线的应用,据说第一个这么做的人是法国数学家费马(Fermat)[7],深入了解可看Richard Courant, Fritz John, Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, Section 3.6, Part b.
Morris Kline, Calculus : an intuitive and physical approach, second edition, Chapter 4,Section 1 ↩︎
Richard Courant, Fritz John, Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, P156 ↩︎
Morris Kline, Calculus : an intuitive and physical approach, second edition, Chapter 4,Section 2 ↩︎
Richard Courant, Fritz John, Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, P156 ↩︎
Courant and Robbins, What Is Mathematics? Second Edition, P415 ↩︎
Richard Courant, Fritz John, Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, Section 3.6, Part b ↩︎
Courant and Robbins, What Is Mathematics? Second Edition, P418 ↩︎