图表的重要性:Anscombe的四组数据
1973年,统计学家F.J. Anscombe构造出了四组奇特的数据。它告诉人们,在分析数据之前,描绘数据所对应的图像有多么的重要。
| I | II | III | IV | ||||
|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | x | y |
| 10.0 | 8.04 | 10.0 | 9.14 | 10.0 | 7.46 | 8.0 | 6.58 |
| 8.0 | 6.95 | 8.0 | 8.14 | 8.0 | 6.77 | 8.0 | 5.76 |
| 13.0 | 7.58 | 13.0 | 8.74 | 13.0 | 12.74 | 8.0 | 7.71 |
| 9.0 | 8.81 | 9.0 | 8.77 | 9.0 | 7.11 | 8.0 | 8.84 |
| 11.0 | 8.33 | 11.0 | 9.26 | 11.0 | 7.81 | 8.0 | 8.47 |
| 14.0 | 9.96 | 14.0 | 8.10 | 14.0 | 8.84 | 8.0 | 7.04 |
| 6.0 | 7.24 | 6.0 | 6.13 | 6.0 | 6.08 | 8.0 | 5.25 |
| 4.0 | 4.26 | 4.0 | 3.10 | 4.0 | 5.39 | 19.0 | 12.50 |
| 12.0 | 10.84 | 12.0 | 9.13 | 12.0 | 8.15 | 8.0 | 5.56 |
| 7.0 | 4.82 | 7.0 | 7.26 | 7.0 | 6.42 | 8.0 | 7.91 |
| 5.0 | 5.68 | 5.0 | 4.74 | 5.0 | 5.73 | 8.0 | 6.89 |
这四组数据中,x值的平均数都是9.0,y值的平均数都是7.5;x值的方差都是10.0,y值的方差都是3.75;它们的相关度都是0.816,线性回归线都是y=3+0.5x。单从这些统计数字上看来,四组数据所反映出的实际情况非常相近,而事实上,这四组数据有着天壤之别。
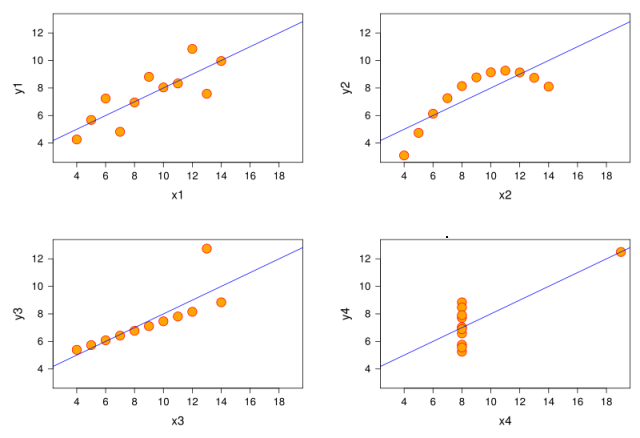
把它们描绘在图表中,你会发现这四组数据是四种完全不同的情况。第一组数据是大多人看到上述统计数字的第一反应,是最“正常”的一组数据;第二组数据所反映的事实上是一个精确的二次函数关系,只是在错误地应用了线性模型后,各项统计数字与第一组数据恰好都相同;第三组数据描述的是一个精确的线性关系,只是这里面有一个异常值,它导致了上述各个统计数字,尤其是相关度值的偏差;第四组数据则是一个更极端的例子,其异常值导致了平均数、方差、相关度、线性回归线等所有统计数字全部发生偏差。
来源:
http://www.reddit.com/r/math/comments/9fz3u/4_datasets_that_demonstrate_the_importance_of/
http://en.wikipedia.org/wiki/Anscombe’s_quartet
方差,通俗点讲,就是和中心偏离的程度!用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)并把它叫做这组数据的方差。记作S2。 在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。