zoukankan      html  css  js  c++  java

  • 码农干货系列【10】光线追踪进阶:javascript玩转3D纹理映射

    17205735-13eeab7f28c647548f5218bdc77d6050

    简介

    本文在光线追踪的基础之上，为了追求渲染速度和效率，去除了光线的反射、去除了透视投影（如我前面两篇干货8和干货9，所以渲染虽然是3D场景，其实不是真实看到的，但不影响实验），进行了一些有趣的尝试。此文将分享这两天尝试的成果：3D雕刻。

    3D雕刻，顾名思义--在3D物体上进行雕刻，所以要达到的目的不仅仅是渲染几种常见的几何形状，还包括在几何形状上绘制、绘画等等。本文依旧使用大家熟悉的javascript语言，HTML5 canvas作为显示屏。

    在读本文之前，最好可以了解一些下面这些基础知识:

    正交投影

    线性代数基础

    数据结构和算法

    javascript基础知识

    射线、AABB、面、球体之间碰撞检测算法

    透视投影（本文虽然略去了canvas和影像屏的mapping,使用了固定视锥体去渲染，所以下面的的demo不建议去修改eye的坐标）

    Vector3的几何意义(使用时候要区分什么时候代表点，什么时候代表向量)

    Canvas像素操作getImageData/putImageData/跨域、渐变createLinearGradient、绘制文字fillText、图片drawImage/base64等

    如果不了解上面相关的内容，可以做一些search，或者通过本文做一些熟悉。

    Vector3类

    这个类是最常用的类了。最重要的一点就使用的时候理解它是代表点还是向量，以及各个方法的几何意义。

    var Vector3 = function (x, y, z) { this.x = x; this.y = y; this.z = z; };
Vector3.prototype = {
    dot: function (v) { return this.x * v.x + this.y * v.y + this.z * v.z; },
    sub: function (v) { return new Vector3(this.x - v.x, this.y - v.y, this.z - v.z); },
    normalize: function () { return this.divideScalar(this.length()); },
    divideScalar: function (s) { return new Vector3(this.x / s, this.y / s, this.z / s); },
    length: function () { return Math.sqrt(this.x * this.x + this.y * this.y + this.z * this.z); },
    sqrLength: function () { return this.x * this.x + this.y * this.y + this.z * this.z; },
    multiplyScalar: function (s) { return new Vector3(this.x * s, this.y * s, this.z * s); },
    add: function (v) { return new Vector3(this.x + v.x, this.y + v.y, this.z + v.z); },
    cross: function (v) { return new Vector3(-this.z * v.y + this.y * v.z, this.z * v.x - this.x * v.z, -this.y * v.x + this.x * v.y); },
    round: function () { return new Vector3(Math.round(this.x), Math.round(this.y), Math.round(this.z)) },
    distanceTo: function (v) {   return Math.sqrt(this.distanceToSquared(v)); },
    distanceToSquared: function (v) {   var dx = this.x - v.x;   var dy = this.y - v.y; var dz = this.z - v.z;
       return dx * dx + dy * dy + dz * dz;
    }
}

    题外话：为什么Vector3?为什么不用齐次坐标Vector4?（主要是因为没有透视投影的过程了。）

    var Vector4 = function ( x, y, z, w ) {
    this.x = x || 0;
    this.y = y || 0;
    this.z = z || 0;
    this.w = w || 1;
}

    Vector4的最后一个参数w是干什么的？为什么不使用4*4矩阵？为什么是4*4？不是3*3?

    “齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”

                                                                                                                             —— F.S. Hill, JR

    有了w,可以进行透视除法，隐藏面消除等算法。那怎么才能知道w?

    把3*3的矩阵扩大成4*3的矩阵==>增加的那个维度可以用来进行w的计算；

    线性代数的基础是过原点，向量是标量的数组，矩阵是向量的数组，把4*3的矩阵扩大成4*4的矩阵==>增加的那个维度可以用来表示平移。

    所以：利用齐次坐标技术来描述空间各点的坐标，用4*4的矩阵来解决空间各点的变换，已经成了计算机图形学的一个标准。

                                                                           -----摘自《HTML5实验室:Canvas世界》

    射线与正方体碰撞检测

    为了简单起见，本文出现的cube都属于AABB,不属于OBB。为了渲染正方体，首先需要推导出射线与正方体是否相交和交点坐标。

    rp1

    使用矩形的中心点和边长表示这个矩形：

    var Cube = function (center, length) {
    this.center = center;
    this.length = length;
    this.hLength = length / 2;

    this.minX = this.center.x - this.hLength;
    this.maxX = this.center.x + this.hLength;
    this.minY = this.center.y - this.hLength;
    this.maxY = this.center.y + this.hLength;
    this.minZ = this.center.z - this.hLength;
    this.maxZ = this.center.z + this.hLength;
}

    使用射线的起点和方向表示射线：

    Ray3 = function (origin, direction) {
    this.origin = origin;
    this.direction = direction;
}

Ray3.prototype = {
    getPoint: function (t) {
        return this.origin.add(this.direction.multiplyScalar(t));
    }
}

    给定射线和正方体之后，分6次求出射线也正方体六个面（无区域限制）的交点，如果有交点，再判断该交点是否在正方体矩形面之内。都满足的话，判定为相交。如下面代码所示：

    Cube.prototype.intersect = function (r3) {
    var d = r3.direction, p1 = r3.origin;
    var irs = [];
    var ir1 = this.getTIntersectPlane(p1, d, "z", this.center.z - this.hLength);
    var ir2 = this.getTIntersectPlane(p1, d, "z", this.center.z + this.hLength);
    var ir3 = this.getTIntersectPlane(p1, d, "x", this.center.x - this.hLength);
    var ir4 = this.getTIntersectPlane(p1, d, "x", this.center.x + this.hLength);
    var ir5 = this.getTIntersectPlane(p1, d, "y", this.center.y - this.hLength);
    var ir6 = this.getTIntersectPlane(p1, d, "y", this.center.y + this.hLength);

    if (ir1) irs.push(ir1);
    if (ir2) irs.push(ir2);
    if (ir3) irs.push(ir3);
    if (ir4) irs.push(ir4);
    if (ir5) irs.push(ir5);
    if (ir6) irs.push(ir6);

    if (irs.length === 1) {
        return irs[0].cp;
    }
    else if (irs.length === 2) {
        if (irs[0].t > irs[1].t) return irs[1].cp;
        if (irs[1].t > irs[0].t) return irs[0].cp;
    }

    return null;
}

Cube.prototype.getTIntersectPlane = function (p1,d,type,value) {

    var _intersectResult = [];
    var t, cp;
    if (type === "z")
    {     
        t= (value - p1.z) / d.z;
        cp = p1.add(d.multiplyScalar(t));       
        if (cp.x < this.maxX && cp.x > this.minX && cp.y < this.maxY && cp.y > this.minY) return { t: t, cp: cp };
    }
    if (type === "x") {
         t = (value - p1.x) / d.x;
         cp = p1.add(d.multiplyScalar(t));
         if (cp.z < this.maxZ && cp.z > this.minZ && cp.y < this.maxY && cp.y > this.minY) return { t: t, cp: cp };
    }
    if (type === "y") {
         t = (value - p1.y) / d.y;
         cp = p1.add(d.multiplyScalar(t));
         if (cp.x < this.maxX && cp.x > this.minX && cp.z < this.maxZ && cp.z > this.minZ) return { t: t, cp: cp };
    }

    return null;
}

    可以想象，直线与正方体的交点只可能是两个或者一个。所以当交点为两个的时候，最后返回离射线发射点近的相交点，该点才是先与正方体相交的点。

     if (irs[0].t > irs[1].t) return irs[1].cp;
 if (irs[1].t > irs[0].t) return irs[0].cp;

    渲染测试（在上篇球的基础上加入正方体）:

    请使用现代浏览器，你的浏览器过时了！下载地址http://dl.pconline.com.cn/download/51614.html

    修改球的半径、正方体的边长等参数==>

    绘制渐变文字

    要在正方体的外表面绘制文字，先尝试在canvas中绘制渐变文字。canvas提供了createLinearGradient方法来设置fillStyle为渐变色,然后使用fillText来绘制文字。如下所示:

    var linearText = ctx.createLinearGradient(0, 0, 200, 200);
linearText.addColorStop(0, "blue");
linearText.addColorStop(0.5, "yellow");
linearText.addColorStop(1, "red");
ctx.fillStyle = linearText;
var fontSize = fontSize || "200px";
ctx.font = "bold 200px Arial";
ctx.textBaseline = "top";
ctx.fillText("当", 0, 0);

    效果如下所示:



    修改显示的文字和字体大小==>

    2D文字Mapping立方体表面

    因为要在正方体表面绘制文字，所以在把2D文字里面每个像素的坐标和颜色保存起来，然后对应到正方体的表面。所以专门创建了一个方法createWordData来生成文字像素坐标和颜色信息：

    function createWordData(word) {
    var canvas = document.createElement("canvas");
    canvas.width = 90;
    canvas.height = 90;
    var ctx = canvas.getContext("2d");

    var linearText = ctx.createLinearGradient(0, 0, 90, 90);
    linearText.addColorStop(0, "blue");
    linearText.addColorStop(0.5, "yellow");
    linearText.addColorStop(1, "red");
    ctx.fillStyle = linearText;
    ctx.font = "bold 70px Arial";
    ctx.textBaseline = "top";
    ctx.fillText(word, 20, 15);

    var imgdata = ctx.getImageData(0, 0, canvas.width, canvas.height);
    var pixels = imgdata.data, tempN = 0;
    var wordData = [];
    for (var y = 0; y < canvas.height; y++) {
        for (var x = 0; x < canvas.width; x++) {
            if (pixels[tempN + 3] !== 0) {
                wordData.push({ position: { x: x, y: y }, color: [pixels[tempN], pixels[tempN + 1], pixels[tempN + 2], pixels[tempN + 3]] })
            }
            tempN += 4;
        }
    }

    return wordData;
}

    这里使用提取方式是：遍历每个像素的rgba中的a是否是0，如果不是0，则判定为在字的像素坐标范围。如果写过canvas库的经历的话，这种方式一定不陌生，一些点击操作精确到像素级别的时候，用如下的方式去判定：

    p._testHit = function (ctx) {
    try {
        var hit = ctx.getImageData(0, 0, 1, 1).data[3] > 1;
    } catch (e) {
            throw "An error has occurred. This is most likely due to security restrictions on reading canvas pixel data with local or cross-domain images.";
    }
    return hit;
}

    题外话：在写canvas库的时候发现，谷歌浏览器精确到像素非常快，而IE9/10精确像素非常慢，包括win8上的webapp/webgame壳（微软webapp/webgame套上该壳就是native的）也非常非常慢，每次点击都掉帧，点得越快，掉得越快。因为精确到像素涉及到了一些矩阵变换，所以IE该好好优化优化了，或者基于webkit二次开发吧，落后Chrome好多好多了。

    创建完三个文字数据信息，把三个字mapping到正方体的三个面：正面、右侧面和顶部表面。

    当mapping正面时：wordX===CubeX(相对于左上角，下面一样)、wordY===CubeY(相对于左上角，下面一样)

    当mapping右侧面时：wordX===CubeZ、wordY===CubeY

    当mapping顶部表面时：wordX===CubeX、wordY===CubeZ

    所以有：

    var color = null;
for (var k = 0, l = word1.length; k < l; k++) {
    var dD = word1[k];
    if (Math.round(result2.y) === cube.maxY && Math.round(result2.x - cube.minX) === dD.position.x && Math.round(result2.z - cube.minZ) === dD.position.y) {
        color = dD.color;
        break;

    }
}
if (!color) {
    for (var k = 0, l = word2.length; k < l; k++) {
        var dD = word2[k];
        if (Math.round(result2.z) === cube.maxZ && Math.round(result2.x - cube.minX) === dD.position.x && Math.round(cube.maxY - result2.y) === dD.position.y) {
            color = dD.color;
            break;

        }
    }
}
if (!color) {
    for (var k = 0, l = word3.length; k < l; k++) {
        var dD = word3[k];
        if (Math.round(result2.x) === cube.maxX && Math.round(cube.maxY - result2.y) === dD.position.y && Math.round(cube.maxZ - result2.z) === dD.position.x) {
            color = dD.color;
            break;

        }
    }
}

    渲染测试效果如下:

    请使用现代浏览器，你的浏览器过时了！下载地址http://dl.pconline.com.cn/download/51614.html

    修改各个参数试试( 这个有点久，耐心等会儿，或者使用chrome浏览器)==>

    2D图片Mapping立方体表面

    图片的mapping也是同样的道理。不同的地方的，由于getImageData会报跨域的安全问题，所以会受到限制。这里把图片进行base64编码，然后绘制到canvas当中去。

    效果如下所示：

    请使用现代浏览器，你的浏览器过时了！下载地址http://dl.pconline.com.cn/download/51614.html

    通过 这个网站 把64*64的图标转成base64然后粘贴进来 (这个有点久，耐心等会儿，或者使用chrome浏览器)
    （要以data:image/png;base64,开头,别把整个img粘贴进textarea）
    ps:这里还有一只base64企鹅http://1.iamzhanglei.sinaapp.com/base64.html

    雕刻球体

    最后，要做的是在球体表面进行2D雕刻。这里涉及到正交投影的问题。如下图所示:

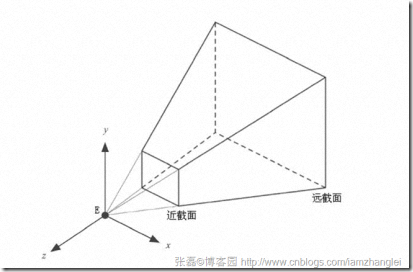
    透视投影：

    201110230819366352 

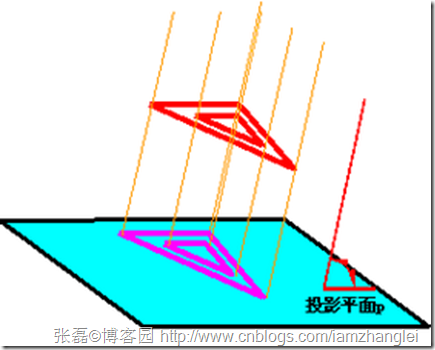
    正交投影：

    201110230819372514

    这里值得注意的地方是，球体雕刻渲染的管线如下步骤：

    1.在球体的正面放上一个垂直地面的正方形平面（可以理解为正方体的正面），

    2.假定文字绘制到正方形平面，

    3.正方形上的文字通过正交投影至球体表面。

    所以，通过所以正面形平面上有像素的点，发射一条平行于地面（y=0）的射线（可以得到，ray3的方向为（0，0，-1））打在球体表面，这个时候影像平面是球体表面。所以下面的方法用于保存所有射线通过正交投影打在球体表面上的点：

    function generateWordToBall(word1, word2, word3, ball, cube) {
    var color = null;
    var bca = [];
    for (var k = 0, l = word1.length; k < l; k++) {
        var dD = word1[k];
        var r3 = new Ray3(new Vector3(cube.minX + dD.position.x - 20, cube.maxY - dD.position.y + 30, cube.maxZ), new Vector3(0, 0, -1));
        var result3 = ball.intersect(r3);
        if (result3)
            bca.push({ cp: result3.round(), cl: dD.color });
    }

    for (var k = 0, l = word2.length; k < l; k++) {
        var dD = word2[k];
        var r3 = new Ray3(new Vector3(cube.minX + dD.position.x - 60, cube.maxY - dD.position.y, cube.maxZ), new Vector3(0, 0, -1));
        var result3 = ball.intersect(r3);
        if (result3)
            bca.push({ cp: result3.round(), cl: dD.color });
    }

    for (var k = 0, l = word3.length; k < l; k++) {
        var dD = word3[k];
        var r3 = new Ray3(new Vector3(cube.minX + dD.position.x, cube.maxY - dD.position.y - 20, cube.maxZ), new Vector3(0, 0, -1));
        var result3 = ball.intersect(r3);
        if (result3)
            bca.push({ cp: result3.round(), cl: dD.color });
    }

    return bca;
}

    拿到这些点之后，剩下的就很简单明了。只需把从视点发出去的射线与球体的交点和bca中的对比，如果在bca当中有，则绘制对应文字像素的颜色，在此不再阐述分析。

    在线演示

    请使用现代浏览器，你的浏览器过时了！下载地址http://dl.pconline.com.cn/download/51614.html

    that's all.Have fun!
  • 相关阅读:
    bzoj1096 [ZJOI2007]仓库建设
    bzoj2054 疯狂的馒头
    bzoj1597 [Usaco2008 Mar]土地购买
    【洛谷P1083】[NOIP2012]借教室
    【洛谷P1367】蚂蚁
    【洛谷P1886】滑动窗口
    【洛谷P2216】[HAOI2007]理想的正方形
    【题解】洛谷P2914[USACO08OCT]断电Power Failure
    【数据结构】数组模拟链表
    【题解】洛谷P1002过河卒
  • 原文地址：https://www.cnblogs.com/iamzhanglei/p/2965334.html
Copyright © 2011-2022 走看看