Java实现迷宫和八皇后

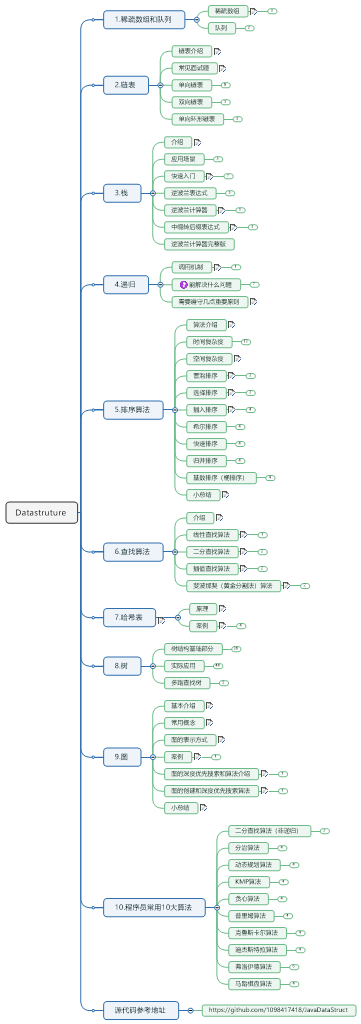
该文章主要是介绍两个递归的demo（迷宫问题和八皇后）

迷宫问题

/**
 * @desc 迷宫问题
 * 1.初始化一个8行7列的矩阵 map[8][7]
 * 2.假设：
 * （1）三种类型：0-还没有走,1-档板,2-可以走（已走）,3-走不通
 * （2）策略：下-》右-》下-》左
 * （3）初始值：周围都是1
 * 3.过程分析：
 * （1）已经找到（确定找到的条件：第7行6列即为找到 =》 [6,5]=2）
 * （2）还没有找到按策略去找
 *
 * @Author xw
 * @Date 2019/9/3
 */
public class MingGong {
    public static void main(String[] args) {
        // 1.初始化一个8行7列的矩阵arr[8][7]
        int[][] map = new int[8][7];
        // 2.初始值：周围都是1
        // 第1行和第8行设置档板
        for (int j = 0; j < 7; j++) {
            map[0][j] = 1;
            map[7][j] = 1;
        }
        // 第1列和第7列设置档板
        for (int i = 0; i < 8; i++) {
            map[i][0] = 1;
            map[i][6] = 1;
        }
        // 输出矩阵
        print(map);
        System.out.println("-------------------------");
        // 设置档板 [3,1]=1,[3,2]=1
        map[3][1] = 1;
        map[3][2] = 1;
        print(map);
        // 策略：下-》右-》上-》左
        setWay(map, 1, 1); // 从[1,1]这个位置开始
        System.out.println("策略:下-》右-》上-》左 =>");
        print(map);
    }
}

八皇后

/**
 * @desc 8皇后问题
 * 1.是什么？
 *  8x8的矩阵，任意两个位置不能处于同一行、同一列或同一斜线，能找出多少种解法，这就是8皇后问题
 * 2.思路分析
 * （1）第一个皇后放第一行第一列[0,0]
 * （2）第二个皇后放第二行第一列[1,0]...直到判断ok，
 *      如果不ok，继续放在第二列、第三列、依次把所有列放完，找到一个合适位置
 * （3）继续第三个皇后，还是第一列、第二列...直到第8个皇后也放在一个不冲突的位置，
 *      算是找到一个正确解
 * （4）当得到一个正确解时，在栈回退到上一个栈时，就会开始回溯，即将第一个皇后，放在第一列的所有正确解，全部得到
 * （5）然后回头继续第一个皇后放第二列，后面继续循环执行1-4步骤
 * 3.说明
 *  理论上创建一个二维数组来表示一个棋盘，但实际上可以通过算法，
 *  用一个一维数组即可解决 arr[8] = {0, 4, 7, 5, 2, 6, 1, 3}
 *  // arr[0] = 0 表示第1个皇后（第一行）放在第1列，即[0,0]
 *  // arr[1] = 4 表示第2个皇后（第二行）放在第5列，即[1,4]
  * 下标表示第几行 即第几个皇后
 *  arr[i] = val，val表示第i+1个皇后放在第i+1行的第val+1列
 * @Author xw
 * @Date 2019/9/4
 */
public class Queen8 {
    private int max;
    private int[] arr;
    private int count;
    public Queen8(int max) {
        this.max = max;
        this.arr = new int[max];
    }
    public static void main(String[] args) {
        for (int i = 0; i < 8; i++) {
            System.out.print(String.format("R%s	", i+1));
        }
        System.out.println();
        Queen8 queen8 = new Queen8(8);
        queen8.check(0);
        System.out.println(String.format("共有%s种解法", queen8.count));
    }
}

gitee地址：https://gitee.com/linestyle007/jucdemo2

博客地址：https://linestyle007.gitee.io/

github地址：https://github.com/line007/jucdemo2