a.
给俩数, 求他俩之间二进制数中1最多的,有多个输出最小的;
贪心,从小到大加能加就加,最后可能碰到一个不能加了但是当前数比l小,那么就加上这个数,然后从大到小,能减就减,见到符合条件

#include<iostream> #include<stdio.h> #include<string.h> using namespace std; int main(){ long long n, l, r; long long a[100]; long long s = 1, maxa = 1e18; long long u; for(long long i = 0;; i++){ a[i] = s; s*=2; u = i; if(s > maxa)break; } //for(int i = 0; i <= u; i++)printf("%lld ", a[i]); cin>>n; while(n--){ cin>>l>>r;//printf("*%d", u); long long sum = 0; for(int i = 0; i <= u; i++){ if(sum + a[i] <= r){//cout<<sum<<" "<<a[i]<<endl; sum += a[i]; }else if(sum < l){ sum += a[i]; for(int k = i-1; k >= 0; k--){ if(sum - a[k] >= l){ sum -= a[k]; } if(l <= sum && sum <= r) break; }break; } } cout<<sum<<endl; } }
You are given a sequence a consisting of n integers. Find the maximum possible value of 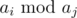 (integer remainder of ai divided by aj), where 1 ≤ i, j ≤ n and ai ≥ aj.
(integer remainder of ai divided by aj), where 1 ≤ i, j ≤ n and ai ≥ aj.
The first line contains integer n — the length of the sequence (1 ≤ n ≤ 2·105).
The second line contains n space-separated integers ai (1 ≤ ai ≤ 106).
想了半天决定看别人代码, 果然在ai的数据范围上做文章了,就是每次处理出来小于等于i的数中最大的保存到一个数组里,然后找每个小于ai的n倍-1的最大数字,取膜

#include<iostream> #include<stdio.h> using namespace std; const int maxa = 2000005; int a[maxa], b[maxa]; int main(){ int n; scanf("%d", &n); while(n--){int x;scanf("%d", &x);a[x] = x;}; for(int i = 1; i < maxa; i++) b[i] = max(b[i-1],a[i]); int maxn = 0; for(int i = 2; i < maxa; i++) if(a[i]) for(int k = 2*i; k < maxa; k+= i) maxn = max(maxn, b[k-1] % i); printf("%d", maxn); }
In a kindergarten, the children are being divided into groups. The teacher put the children in a line and associated each child with his or her integer charisma value. Each child should go to exactly one group. Each group should be a nonempty segment of consecutive children of a line. A group's sociability is the maximum difference of charisma of two children in the group (in particular, if the group consists of one child, its sociability equals a zero).
The teacher wants to divide the children into some number of groups in such way that the total sociability of the groups is maximum. Help him find this value.
The first line contains integer n — the number of children in the line (1 ≤ n ≤ 106).
The second line contains n integers ai — the charisma of the i-th child ( - 109 ≤ ai ≤ 109).
Print the maximum possible total sociability of all groups.
简单的来说题意就是给你一段数字,让你分成任意段,每段的值是这一段中的最大值减去最小值,求所有段的值的最大和;
好吧这题也是看别人的代码看了半天才懂;
由于每段的值是最大值-最小值
我们这样定义三个状态,dp[i][1]代表到以i结尾的值;
dp[i][0]代表当前段的最大值已经确定的最大值(这里的值是确定的最大值+前面区段的值)
dp[i][2]代表当前段的最小值是a[i]的值减去a[i];(同上)
那么dp[i][0]可以由dp[i-1][0]过来代表此数字被放弃了,也可以由dp[i-1][1]推过来代表当前区段的最大值为当前数,在这两个中取最大值;
dp[i][1],dp[i][2]同上

#include<iostream> #include<string.h> #include<stdio.h> using namespace std; const long long maxa = 1000005; long long a[maxa]; long long dp[maxa][3]; int main(){ long long n; cin>>n; long long x; //scanf("%d", &x); cin>>x; dp[1][0] = x; dp[1][2] = -x; for(long long i = 2; i <= n; i++){ cin>>x; for(long long k = 0; k < 3; k++){ dp[i][k] = dp[i-1][k]; if(k > 0) dp[i][k] = max(dp[i][k], dp[i-1][k-1] - x); if(k < 2) dp[i][k] = max(dp[i][k], dp[i-1][k+1] +x); //printf("%d ", dp[i][k]); }//puts(""); }cout<<dp[n][1]<<endl; }
