欢迎关注个人公众号摸鱼范式

FIFO深度计算
作者:星雨夜澈
声明:欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。
数字IC设计中我们经常会遇到这种场景,工作在不同时钟域的两个模块,它们之间需要进行数据传递,为了避免数据丢失,我们会使用到FIFO。当读数据的速率小于写数据的速率时,我们就不得不将那些还没有被读走的数据缓存下来,那么我们需要开多大的空间去缓存这些数据呢?缓存开大了会浪费资源,开小了会丢失数据,如何去计算最小FIFO深度是我们讨论的重点。
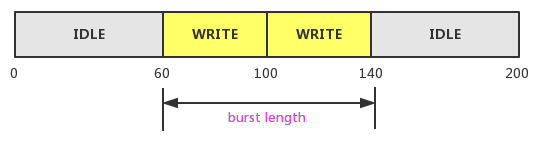
数据突发长度(burst length)
在讲解如何去计算FIFO深度之前,我们来理解一个术语burst length,如果你已经了解了可以跳过。要理解数据的突发长度,首先我们来考虑一种场景,假如模块A不间断的往FIFO中写数据,模块B同样不间断的从FIFO中读数据,不同的是模块A写数据的时钟频率要大于模块B读数据的时钟频率,那么在一段时间内总是有一些数据没来得及被读走,如果系统一直在工作,那么那些没有被读走的数据会越累积越多,那么FIFO的深度需要是无穷大的,因此只有在突发数据传输过程中讨论FIFO深度才是有意义的。也就是说我们一次传递一包数据完成后再去传递下一包数据,我们把一段时间内传递的数据个数称为burst length。在维基百科中,burst transmission是这样解释的:In telecommunication, a burst transmission or data burst is the broadcast of a relatively high-bandwidth transmission over a short period。
我们知道burst length过后,通过上述讨论我们大概就知道FIFO的最小深度与burst rate, burst size, read and write frequency等因素有关。要确定FIFO的深度,关键在于计算出在突发读写这段时间内有多少个数据没有被读走。也就是说FIFO的最小深度就等于没有被读走的数据个数。
其实在一些ASIC论坛中,很多前辈就给出过FIFO深度计算公式,但是当时看到公式时不是太理解它是怎么来的,为了让大家更好的理解FIFO size的计算过程,这里在不套用计算公式的前提下来逐步计算不同场景FIFO深度,当然在本文的最后会给出FIFO深度的计算公式,只想套用公式的同志可以直接移步到本文末尾。
在讨论之前我们假定模块A向FIFO写数据的时钟频率为fa,模块B从FIFO读数据的时钟频率为fb。
场景1:fa>fb with no idle cycles in both write and read
假设:
- 写数据时钟频率fa=80MHz
- 读数据时钟频率fb=50MHz
- 突发长度= number of data to be transferred = 120
- 在突发传输过程中,数据都是连续读写的
那么:
- 写一个数据所需要的时间 = 1/80MHz = 12.5ns
- 突发传输中,写完所有数据所需要的时间 = 120*12.5ns = 1500ns
- 读一个数据所需要的时间 = 1/50MHz = 20ns
- 所以写完所有的突发传输数据需要花费1500ns
- 在1500ns内能够读走的数据个数 = 1500ns/20ns = 75
- 所以在1500ns内还没有被读走的数据个数 = 120-75 = 45
- 因此FIFO的最小深度为45
场景2:fa>fb with two clock cycle delay between two successive read and write
场景2在场景1的基础上增加了一个假设,即读比写慢两拍。这种假设是真正存在的,在异步FIFO设计中,我们需要去判断FIFO的空满来保证逻辑的正确性,判断空满标志需要去比较读写指针,而读指针与写指针处在不同的时钟域中,我们需要采用格雷码和两级同步寄存器去降低亚稳态的概率,而两级同步必然会导致空满标志位的判断至少延迟2个cycle。对于空标志位来说,将写指针同步到读时钟域至少需要花费2个时钟,而在同步这段时间内有可能还会写入新的数据,因此同步后的写指针一定小于或等于(当且仅有同步时间内没有新数据写入的情况下才会等于)当前的写指针,所以此时判断不一定是真空;同理,对于满标志位来说,将读指针同步到读时钟域至少需要花费2个时钟,而在同步这段时间内有可能还会读出新的数据,因此同步后的读指针一定小于或等于当前读指针,所以此时判断并不一定是真满。
通过上述讨论可以知道场景2的FIFO最小深度应该比场景1的FIFO最小深度45略大。
场景3:fa > fb with idle cycles in both write and read
假设:
- 写数据时钟频率fa=80MHz
- 读数据时钟频率fb=50MHz
- 突发长度= number of data to be transferred = 120
- 每隔1个cycle写一次
- 每隔3个cycle读一次
那么:
- 每隔1个cycle写一次,意味着2个cycle才写一个数据
- 每隔3个cycle读一次,意味着4个cycle才读一个数据
- 写一个数据所需要的时间 = 2*1/80MHz = 25ns
- 突发传输中,写完所有数据所需要的时间 = 120*25ns = 3000ns
- 读一个数据所需要的时间 = 4*1/50MHz = 80ns
- 所以写完所有的突发传输数据需要花费3000ns
- 在3000ns内能够读走的数据个数 = 3000ns/80ns = 37.5
- 所以在3000ns内还没有被读走的数据个数 = 120-37.5 = 82.5
- 因此FIFO的最小深度为83
场景4:fa > fb with duty cycles given for wr_enb and rd_enb.
假设:
- 写数据时钟频率fa=80MHz
- 读数据时钟频率fb=50MHz
- 突发长度= number of data to be transferred = 120
- 写使能信号占整个burst时间比重为1/2
- 读使能信号占整个burst时间比重为1/4
那么:
- 场景4与场景3描述不一致,但情形是一致的,因此FIFO的最小深度也为83
场景5:fa < fb with no idle cycles in both write and read
假设:
- 写数据时钟频率fa=40MHz
- 读数据时钟频率fb=50MHz
- 突发长度= number of data to be transferred = 120
- 在突发传输过程中,数据都是连续读写的
那么:
- 由于读数据比写数据要快,因此FIFO只起到过时钟域的作用,FIFO的最小深度为1即可
场景6:fa < fb with idle cycles in both write and read
假设:
- 写数据时钟频率fa=40MHz
- 读数据时钟频率fb=50MHz
- 突发长度= number of data to be transferred = 120
- 每隔1个cycle写一次
- 每隔3个cycle读一次
那么:
- 每隔1个cycle写一次,意味着2个cycle才写一个数据
- 每隔3个cycle读一次,意味着4个cycle才读一个数据
- 写一个数据所需要的时间 = 2*1/40MHz = 50ns
- 突发传输中,写完所有数据所需要的时间 = 120*50ns = 6000ns
- 读一个数据所需要的时间 = 4*1/50MHz = 80ns
- 所以写完所有的突发传输数据需要花费6000ns
- 在6000ns内能够读走的数据个数 = 6000ns/80ns = 75
- 所以在6000ns内还没有被读走的数据个数 = 120-75 = 45
- 因此FIFO的最小深度为45
场景7:fa = fb with no idle cycles in both write and read
假设:
- 写数据时钟频率fa=50MHz
- 读数据时钟频率fb=50MHz
- 突发长度= number of data to be transferred = 120
那么:
- 如果读写时钟同源并且无相位差,那么可以不需要FIFO;否则FIFO的最小深度为1
场景8:fa = fb with idle cycles in both write and read
假设:
- 写数据时钟频率fa=50MHz
- 读数据时钟频率fb=50MHz
- 突发长度= number of data to be transferred = 120
- 每隔1个cycle写一次
- 每隔3个cycle读一次
那么:
- 每隔1个cycle写一次,意味着2个cycle才写一个数据
- 每隔3个cycle读一次,意味着4个cycle才读一个数据
- 写一个数据所需要的时间 = 2*1/50MHz = 40ns
- 突发传输中,写完所有数据所需要的时间 = 120*40ns = 4800ns
- 读一个数据所需要的时间 = 4*1/50MHz = 80ns
- 所以写完所有的突发传输数据需要花费4800ns
- 在4800ns内能够读走的数据个数 = 4800ns/80ns = 60
- 所以在4800ns内还没有被读走的数据个数 = 120-60 = 60
- 因此FIFO的最小深度为60
场景9:Data rates are given,read and write random(important!!!)
在前面几种场景中,我们给的条件都是每隔几个时钟读写一次,这种周期性读写在实际中很常见。但是在工程设计中还存在这样一种情形,只给出数据在一段时间内的读写速率,怎么读写完全随机,这种情况我们需要考虑最坏的一种情况避免数据丢失。在最坏的情形中,读写的速率应该相差最大,也就是说需要找出最大的写速率和最小的读速率。
假设:
- 写数据时钟频率fa=80MHz
- 读数据时钟频率fb=50MHz
- 在写时钟周期内,每100个周期就有40个数据写入FIFO
- 在读时钟周期内,每10个周期可以有8个数据读出FIFO
那么:
- 首先这里没有给出数据的突发长度,从假设中可以得出每100个周期就有40个数据写入FIFO,这里可能就有人会说突发长度就是40个数据,其实不是这样的,因为数据是随机写入FIFO的,我们需要考虑做坏的情形,即写速率最大的情形,只有如下图背靠背的情形才是写速率最高的情形,burst length为80
- 注意:这里需要验证一下是否有解,即写入burst数据时间必须大于等于读出burst数据时间,不然数据就会越累积越多,使得FIFO的深度必须为无穷大。首先写入80个数据需要的时间 = 1/80MHz*(80*100/40)=2500ns,读出80个数据需要的时间 = 1/50MHz*(80*10/8)=2000ns,由于写入burst数据时间大于对出burst数据时间,因此有解。
- 下面来计算FIFO最小深度,连续写入80个数据最快所需要时间 = 1/80MHz * 80 = 1000ns
- 从FIFO中读出一个数据至少所需时间 = (1/50MHz) * (10/8) = 25ns
- 那么在1000ns内能够读出的数据 = 1000ns/25ns = 40
- 在1000ns内没有读出的数据 = 80 - 40 = 40
- 因此FIFO的最小深度为40
总结
从上面分析来看,求FIFO的最小深度主要有以下要点:
- 在求解之前需要验证一下在允许的最大时间长度内写入的数据量是否等于读出的数据量,保证有解;
- 求FIFO深度需要考虑最坏的情形,读写的速率应该相差最大,也就是说需要找出最大的写速率和最小的读速率;
- 不管什么场景,要确定FIFO的深度,关键在于计算出在突发读写这段时间内有多少个数据没有被读走;
- 由于FIFO空满标志位的判断延迟,在实际应用中需要预留一些余量。
下面我们来推导一下FIFO深度的求解公式,假设:
- 写时钟频率为fwr
- 读时钟频率为frd
- 在写时钟周期内,每m个周期内就有n个数据写入FIFO
- 在读时钟周期内,每x个周期内可以有y个数据读出FIFO
那么:
- 首先必须满足(1/fwr)*(m/n) ≥ (1/frd)*(x/y)
- ”背靠背“的情形下是FIFO读写的最坏情形,burst长度 B = 2*n
- 写完burst长度数据最快所需时间 T = (1/fwr)*B
- 从FIFO中读出一个数据至少需要时间 t= (1/frd)*(x/y)
- 在T时间内能够从都走的数据个数 = T/t = B * (frd/fwr)*(y/x)
- 在T时间内还没有读走的数据个数 = B-B* (frd/fwr)*(y/x)
- 因此FIFO的最小深度为 B-B * (frd/fwr)* (y/x)
- 注意保留一些余量