【网络流24题】 2. 太空飞行计划问题 题解

题目链接（洛谷 P2762）

题意：

W 教授正在为国家航天中心计划一系列的太空飞行。每次太空飞行可进行一系列商业性实验而获取利润。现已确定了一个可供选择的实验集合(E = { E_1, E_2, cdots, E_n })，和进行这些实验需要使用的全部仪器的集合(I = { I_1, I_2, cdots, I_n })。实验(E_j)需要用到的仪器是(I)的子集(R_j subseteq I)。

配置仪器(I_k)的费用为(c_k)美元。实验(E_j)的赞助商已同意为该实验结果支付(p_j)美元。W 教授的任务是找出一个有效算法，确定在一次太空飞行中要进行哪些实验并因此而配置哪些仪器才能使太空飞行的净收益最大。这里净收益是指进行实验所获得的全部收入与配置仪器的全部费用的差额。

对于给定的实验和仪器配置情况，编程找出净收益最大的试验计划。

思路：

本题的正解是最小割。这里先引用一下SSL_XXY_BlackCloud大佬的题解，然后我再具体说明一下：

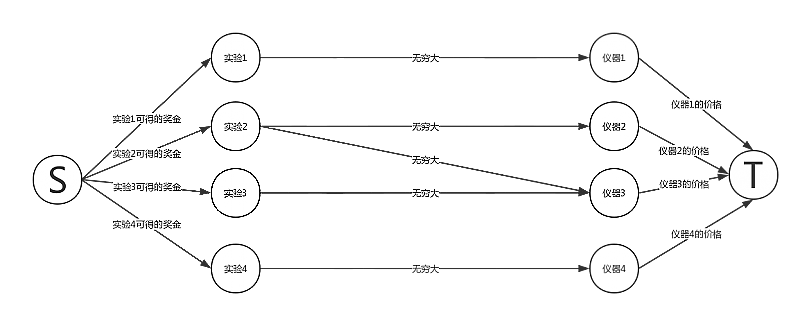
这道题无非是让我们权衡奖金与代价，这两者是有我没他的，怎么去处理呢，我们先建立一张图，所有的实验与源点相连，容量为其奖金，所有的器材与汇点相连，容量为其价格，中间实验与器材相连，容量为无穷大。

这个时候跑最小割，其必定会割掉连接实验或容器的边，因为中间的边的代价为无穷大，一定不会被割掉。

跑最小割相当于选择部分的实验和部分的仪器，剩下的实验和仪器就会被割掉，此时再用实验的总价值减去可能得到的最大值，即为其所要求的答案

如下图 ：

一扶苏一大佬讲到，这个问题抽象一下，是这样的：

给定一个有向图，点有点权，选择一个子图，满足子图上如果选择了一个点就必须选择它后继的所有点。最大化点权和。

这是一个经典的网络流问题，如果一个点被选择了则后继必须被选择，那么称该图是 闭合的，因此该问题叫做最大权闭合子图问题。可以使用最小割解决。

上面说的有点抽象，下面我结合本题的条件说一说为什么可以这样做：

我的理解：

建图的方式就参考SSL_XXY_BlackCloud大佬的题解的连接方式。

首先，最小割割掉的肯定要么是源点连向实验的边（以下简称左侧边），要么是仪器连向汇点的边（以下简称右侧边）。我们先考虑第一次割边。如果被割掉的是左侧边，那么，我们可以理解为，选择此次试验的收益小于成本。反之，如果被割掉的都是右侧边，我们可以理解为，此次试验的收益大于成本。此时流的大小就是我们付出的成本。

我们这样理解成本（一定要理解成本，理解了成本，这道题就变成板题了）：上面提到的答案是所有试验的总价值（注意不是利润）减去最大流（也就是最小割）。也就是说，我们做减法之前，我们只考虑了所有试验的收入，一点也没有考虑支出。那么：

• 如果我们不做某一场试验，我们的成本就是这一场试验的收入（对应上面割左侧边的情况，我们认为不做某一场试验就损失了这一场试验的总收入）；
• 否则，我们的损失就是仪器成本（对应上面割右侧边的情况）。依照上述建图的方法，我们就可以认为，流就是成本。

然后，我们考虑后续割边。我们知道，可以有多场试验对应相同的仪器。那么此时，由于仪器连向汇点的边容量一定是仪器的成本，它只能跑一次，源点连向实验的边同理。这就保证了：

1. 如果多场试验的收入大于这些试验需要仪器的成本，实验仪器的成本只记一次。同时，因为多长试验的收入大于仪器的成本，那么这些仪器到汇点的边一定都是满流量。
2. 如果多场试验的收入少于这些实验仪器的成本，那么一定是源点到这些试验的边满流量，而这些仪器到汇点的边不是满流量的。这保证了我们的成本一定是不做这些试验，而且每场实验的成本也只记录一次。

所以，本题的答案就是实验的总价值（总收入）减去最大流（总成本）。

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
#define root 0
#define target 104

using namespace std;
const int maxn = 105;
const int INF = 0x3f3f3f3f;
int n, m, x, ans;

struct Edge {
    int to, val, nxt;
}e[maxn * maxn * 2];
int numedge, head[maxn], depth[maxn], len_s;
char str[10000];

inline void AddEdge(int from, int to, int val) {
    e[numedge].to = to;
    e[numedge].val = val;
    e[numedge].nxt = head[from];
    head[from] = numedge;
    numedge++;
}

int readint (int &cur, char *ch) {
    int x = 0, f = 1;
    while (ch[cur] > '9' || ch[cur] < '0') {
        if (ch[cur] == '-') f = -1;
        cur++;
        if (cur >= len_s) return 0;
    }
    while (ch[cur] >= '0' && ch[cur] <= '9') {
        x = x * 10 + ch[cur] - '0';
        cur++;
    }
    return x;
}

inline bool bfs() {
    memset(depth, 0, sizeof(depth));
    depth[root] = 1;
    queue<int> q;
    q.push(root);

    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = e[i].nxt) {
            int to = e[i].to;
            if (!depth[to] && e[i].val > 0) {
                depth[to] = depth[u] + 1;
                q.push(to);
            }
        }
    }
    return depth[target] != 0;
}

int dfs(int u, int flow) {
    if (u == target)
        return flow;
    
    for (int i = head[u]; ~i; i = e[i].nxt) {
        int to = e[i].to;
        if (depth[to] > depth[u] && e[i].val > 0) {
            int di = dfs(to, min(flow, e[i].val));
            if (di > 0) {
                e[i].val -= di;
                e[i ^ 1].val += di;
                return di;
            }
        }
    }
    return 0;
}

int Dinic() {
    int res = 0;
    while (bfs()) {
        int d;
        while (d = dfs(root, INF)) {
            res += d;
        }
    }
    return res;
}

int main() {
    memset(head, -1, sizeof(head));
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &x);
        AddEdge(root, i, x);
        AddEdge(i, root, 0);
        ans += x;
        cin.getline(str, 10000);
        len_s = strlen(str);
        int cur = 0;
        while (1) {
            int y = readint(cur, str);
            if (!y) break;
            AddEdge(i, y + n, INF);
            AddEdge(y + n, i, 0);
        }
    }
    for (int i = 1; i <= m; i++) {
        scanf("%d", &x);
        AddEdge(n + i, target, x);
        AddEdge(target, n + i, 0);
    }
    ans -= Dinic();

    for (int i = 1; i <= n; i++)
        if (depth[i] > 0) printf("%d ", i);
    putchar('
');
    for (int i = 1; i <= m; i++)
        if (depth[i + n] > 0) printf("%d ", i);
    printf("
%d
", ans);
    return 0;
}

最后输出的地方可能有点迷。我稍微解释一下：

上述代码是用的Dinic算法。首先，题目保证了这是一个二分图。所以，在最后一次dfs执行结束后，所有该割掉的边流量已经都满了。

但是，此时仍然会额外跑一次BFS。依照代码中BFS的规则：

• 如果是左侧若干实验的边被割，那么，被割的边连接的点一定不会被BFS扫描到（也一定不会因为反向边被扫到。此时图已经不连通了）。
• 如果两个（多个同理）收入相同的实验对应两个仪器，一个实验的收入和这两个仪器的成本相同，如果恰好是某一个实验对应这两个仪器，那么在BFS时，扫描到另一个实验的时候（因为另一个实验啥也没对应，它的边没有被割）会在扫反向边的时候扫到对应仪器的这个实验，也一定是正确的。
• 如果被割掉的是右侧边，那么左侧没有被割掉的实验通过那些容量为INF的边就连向了它们需要的仪器，BFS一定会扫到它们。而用不到的仪器（它们对应实验的边都被割了），因为用到了的仪器连向汇点的边都被割了，所以也无法通过反向边扫到。因此是正确的。

所以，输出此次BFS扫到的点，就是答案（别把超级源点输出了）。