顺序存储和链式存储的区别
都是用来存放相同类型的一组数据元素
不同点
1
顺序存储用数组来实现,一片连续的空间,一个挨着一个放,逻辑上相邻,位置上也相邻。而链式存储,地址不连续,只能通过前后指针来链接关系上的相邻
2
顺序存储,空间节省,只存元素值本身。而链式存储需额外分配空间(4字节),存放提现相应关系的指针。
3
顺序存储时,由数组名和下标确定每个元素,只要下标有效,属于随机访问。而链式存储,必须从头顺着指针顺序访问每一个元素。
4
顺序存储必须保证地址连续,一个挨着一个。所以,可插入删除的位置必须有限范围内限制。而链式存储,无需判断。
5
顺序存储时插入删除需要在指定的位置移动大量的元素,进行实现。而链式存储时,只需要从头顺着指针移动指针找到指定的位置,然后改变前后指针的链接,无需移动元素来进行实现操作。
6
顺序存储时,事先要先开辟一大片连续的空间。必须在该空间的有效范围内进行操作,所以进时要先判满。而链式存储,可以随时根据需要,来开辟增加新节点,无语判断是否存满。
程序由函数组成,函数包括主函数main和自定义函数,实现模块化管理。而算法,就是实现一定功能的自定义函数。
当函数中的参数是简单变量时,实参的值传给形参,形参改变不会影响实参。
当参数为指针变量时,实参的地址传给对应的形参,形参的指向就是实参。形参指向的改变就是实参的改变。当形参为引用时(&),形参就是给对应的实参起的别名,形参实参是一个空间,形参的改变就是实参的改变。属于传址调用。
算法是函数。函数中的参数可以不用输入,通过函数调用中,实参的传递来获得值。
一。无循环,只有简单语句O(1)
多层循环情况,各层循环彼此独立,O(各层最大次数乘积)。内层受外层影响,从过程上分析执行次数,进而求和。
形参为数组时,后面的[]没有任何实际意义,只是数组的标志,传递时,对应的实参一定是该类型数组的数组名(首地址),实参数组的地址传给对应的形参数组,形参数组并没有开辟新的空间,形参就是实参数组。而第二个参数n,就是要对这个数组中的前n个元素进行操作。
数据由数据元素组成,数据元素是数据的基本单位。如果是单数据元素时,数据元素可以直接称为数据。
函数体内定义相同的变量,可以用逗号隔开,定义一次。但是形参中相同类型的变量,必须用逗号隔开,逐个定义。
赋值表达式是把右边的值给左边的变量,整个表达式和变量都是这个值。
定义变量时加&表示引用,引用变量就是给已经定义的变量起别名。与该变量共用一个空间,引用变量的改变就是该变量的改变。
形参变化定义时加&符号,调用时(实参)不加&
静态分配:变量先定义,后使用,一旦定义空间就存在,只有当所在的块({})结束,分配的空间才收回,会出现空间闲置浪费
动态分配:可以根据需要用malloc来开辟,不需要时用free释放,提高空间的利用率。
把a数组中l个元素,放在L中。
if else配对出现,是一个整体,条件成立执行if的,不成立执行else的,如果if后面是普通语句时,else必须有,如果后面是return语句时,表示返回,else可以没有。
为了提现栈的特点,操作栈是,从栈顶元素,逆着到0
数组和广义表
数组某元素的地址=给定元素的地址+从给定元素起到该元素前面的所有的个数×字节数
1
多维数组存放时,追寻一维的规则,一片连续的空间,一个挨着一个放。
2
行序先行后列时,后下标快。列序,先列后行时,前下标快。
3
计算公式时,行序按从前向后展开,列序按从后向前展开。
4
计算每一项时,按该项减起点乘以按展开方向看余下的各项的满。

5
给定的元素与要求的元素在同一方式下存储时,可以直接带公式来求。不同方式下来求时,先根据给定元素的方式,求出首元素的地址(默认为00),然后再带入另一种方式中,求目标元素地址。
6
按序写下标排列时,行序从后向前修改,列序从前向后修改。修改时,一定要在前面操作的基础上,按顺序对该位置进行修改。
7
利用公式求存的下标时,不用计算字节数。
1
三角矩阵比对称矩阵多一个不正常的
2
三角矩阵与对称矩阵在正常区域内的存放都一样
3
不正常的区域内两者不同,对称矩阵是把不对称中的aij映射到正常中的aji(ij互换)。而三角矩阵,是把不正常的这一个直接放到一片连续空间的最后一片空间中。
顺序三元组表
根据非0元素个数,竖着画一片空间,从上到下,从零开始编号。每个空间一分三栏,行号i,列号j,元素值v。按三元组表示,从零填入表内。
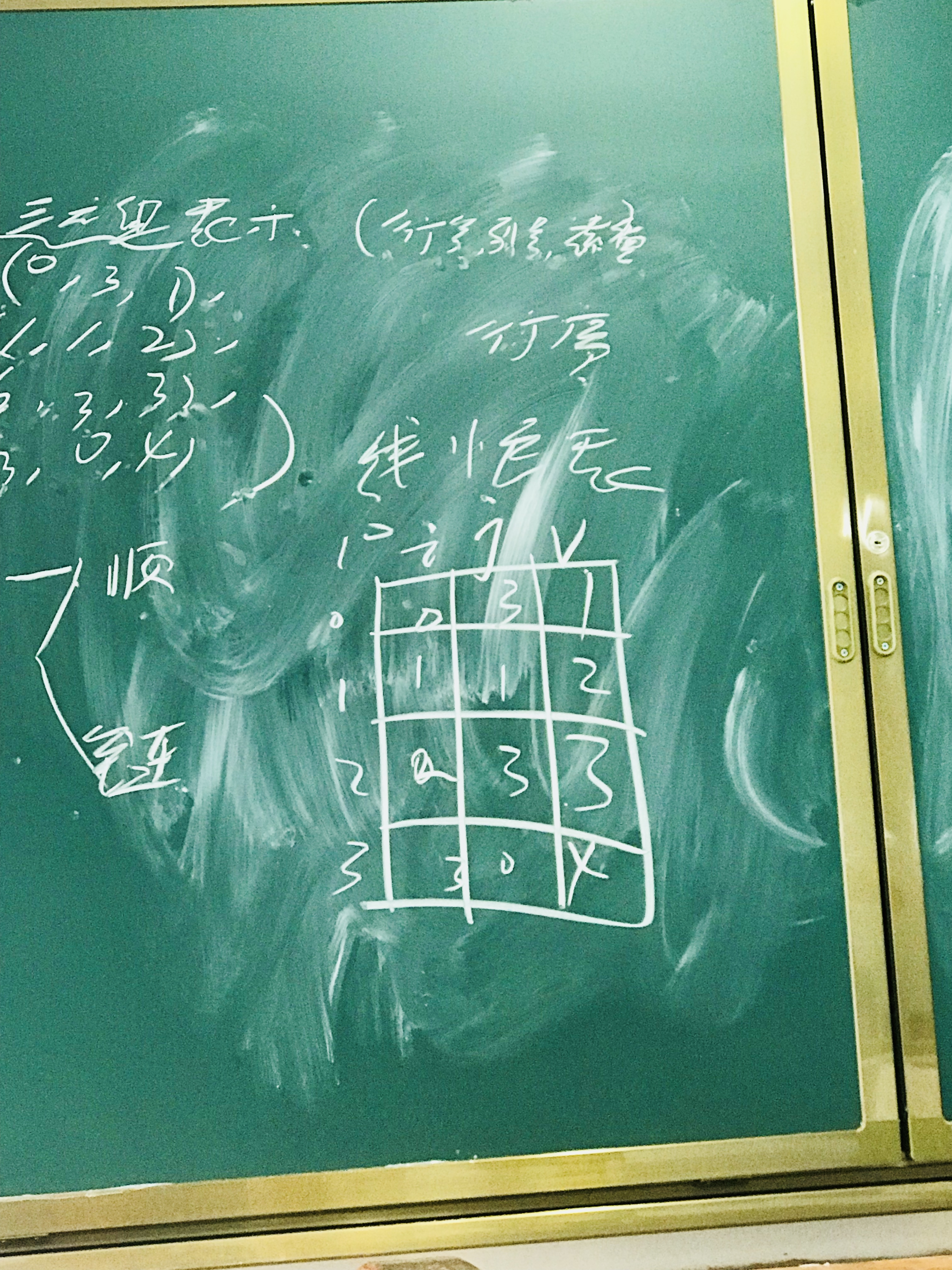
伪地址法
根据非0元素个数,竖着画一片空间,从上到下,从零开始编号。一分两栏,一填伪地址号,二填元素值。对矩阵中所有元素按行序从零开始编号,按行序将非零的编号和元素值从零空间开始填。
带行向量的链式存储法
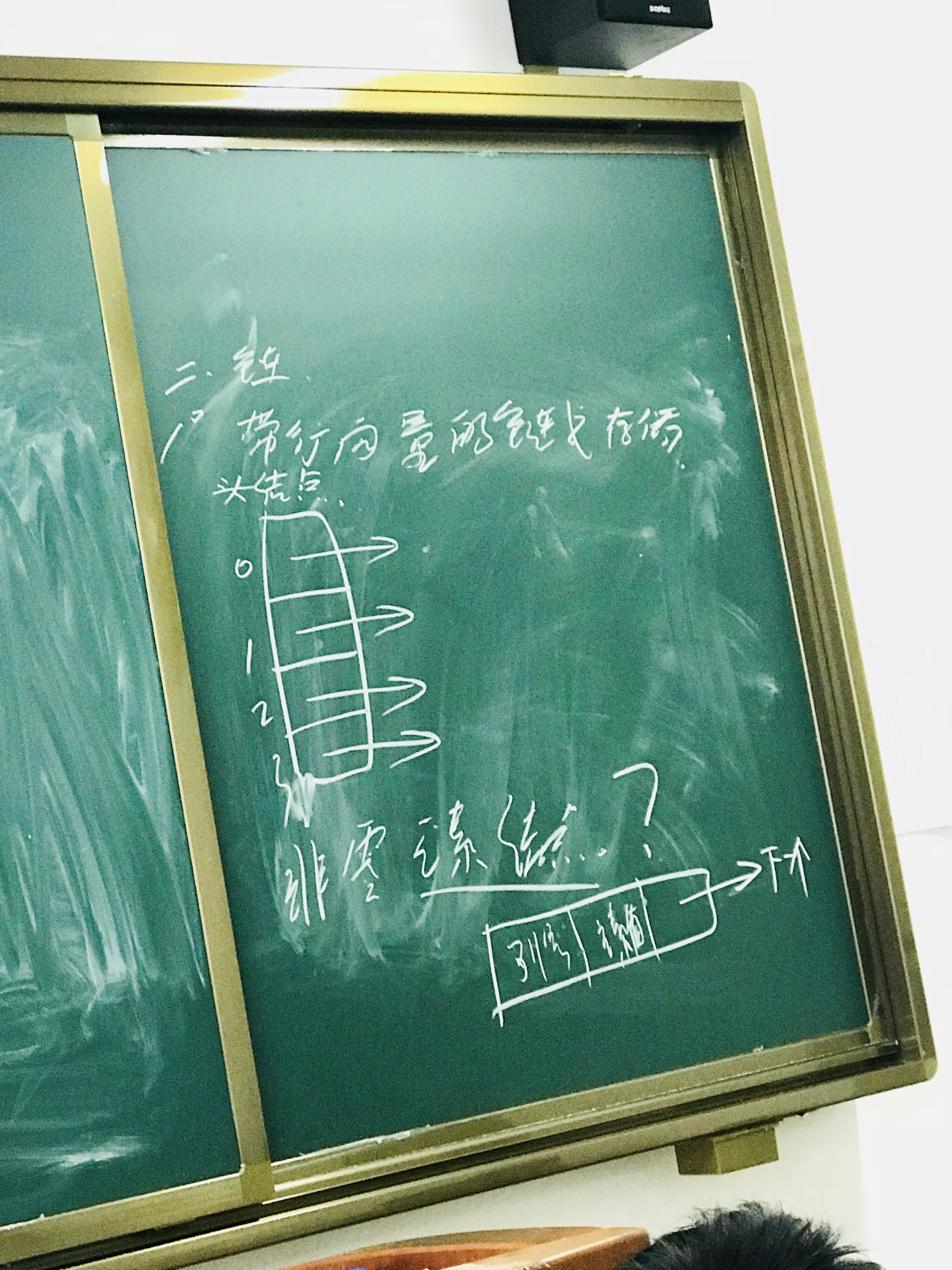
head求表头,tail求表尾,后面紧跟着的括号是参数括号与广义表无关,该括号里边的内容才是真正要求的广义表。
树
树的顺序存储
1竖着画一片连续的空间,根据树中结点数画开,从上到下,从0编号。
2每个空间一分两栏,从0空间开始,从上到下,从左到右依次填入空间的每一栏中。从0空间开始,将第一栏中结点的双亲的下标号,填入第二栏中。根的双亲记为-1。
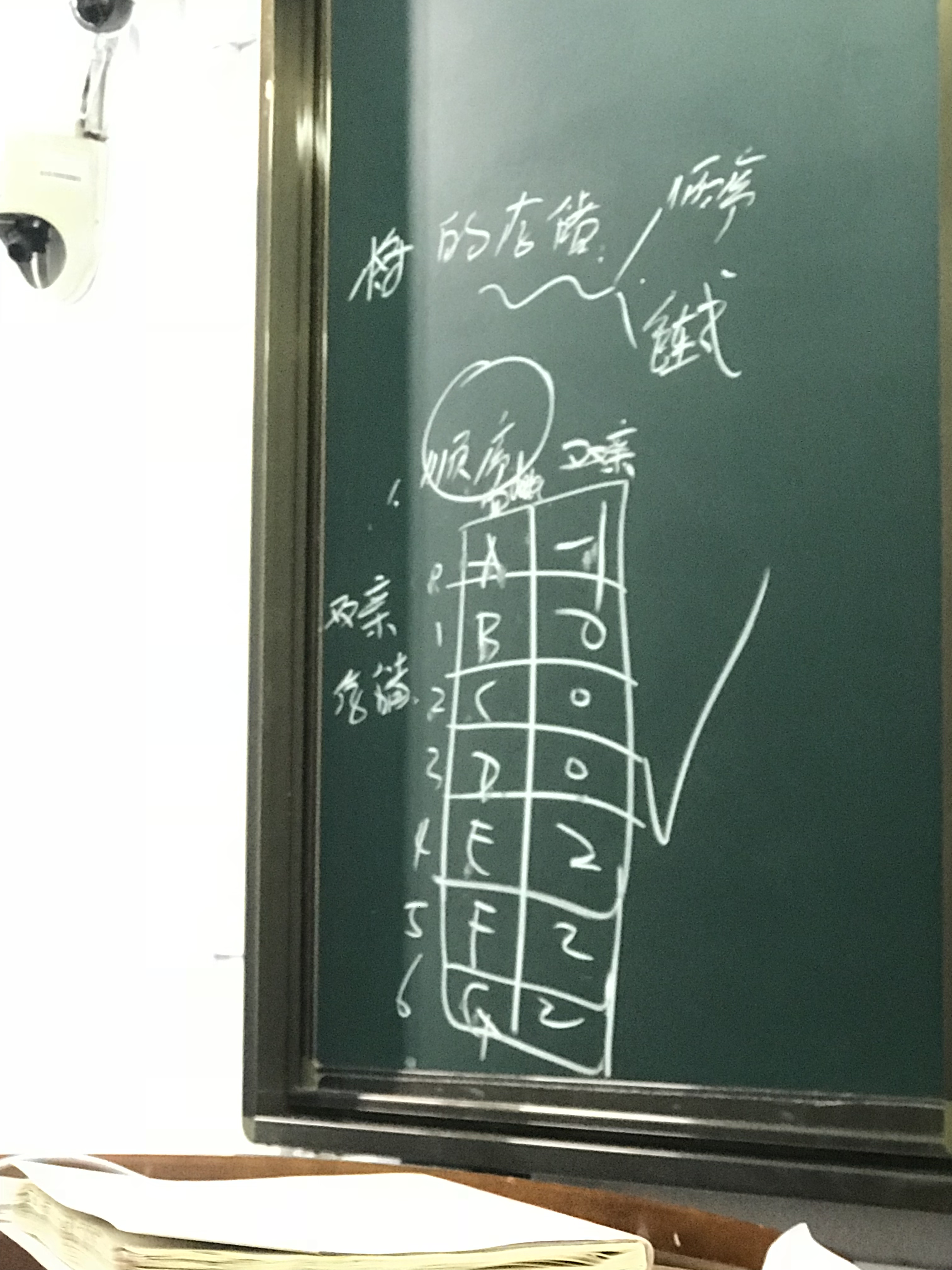
树的链式存储
方法一孩子链存储 树的孩子链为m,树的每个结点m+1,第一部分填它的值,其余部分依次指向它下一层的孩子。(会出现空间浪费的现象)

方法二孩子兄弟链存储 做一个有三个栏的结点,1里面填指向第一个孩子,2里面填值,3里面填同层下一个兄弟。

树的遍历
1先根遍历,根写在最前面,其后根据孩子分块,将孩子依次填入对应块的最前面。
2后根遍历,根写在最后面,其后根据孩子分块,将孩子依次填入对应块的最后面。

二叉树的构造
先在先序确定该块的根,再到中序中以刚刚确定的根为界,划分两块,前为左后为右。(递归)
图的遍历
1深度优先遍历
从某点找第一个未访问的邻结点,从新开始,没有时返回到上一级,直至第一个。
2广度优先遍历
从某点开始,找所有未访问的邻结点,按从左到右顺序访问下一级,自至最后一个。
prim算法,从起点,向外找与内最小的边,添点