上一节介绍了直接插入排序,这一节将介绍冒泡排序(Bubble Sort)。绝大多数程序员接触的第一个排序算法恐怕就是冒泡排序了,(顺便吐槽一下)尤其是被谭浩强的《C程序设计》那本书毒害的一代又一代年轻人,其中也包括我自己,所以现在我一想起大一时学C语言的痛苦经历,往事真是不堪回首,回首起来简直就是痛心疾首!谭书最大的问题就是代码风格很差,或者说根本就没有代码风格,完全不是写给真正的程序员的书。幸运的是,在我的第一份工作中,当时所加入的工作团队非常讲究C代码风格,从那时起我学会了如何写整洁优雅可读性良好的代码,因此对谭书格外反感。 好了,言归正传,冒泡排序又叫做起泡排序,是最简单的交换排序(Swap Sort)。而交换排序的基本思想是两两比较待排序对象的关键字,如果发生逆序(即排列顺序与排序后的次序正好相反),则交换之,直到所有对象都排好序为止。
冒泡排序的基本思想
每次比较两个相邻的元素,如果它们的顺序错误就把它们交换过来。对于从小到大的排序,越大的元素越靠后。
典型的冒泡排序过程看起来是这样子滴, 【图片来源: https://en.wikipedia.org/wiki/Bubble_sort】
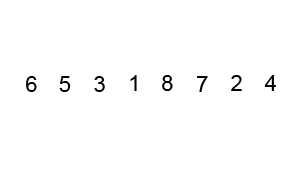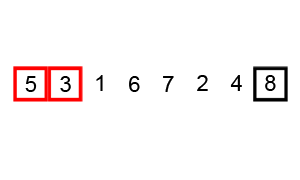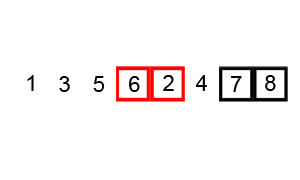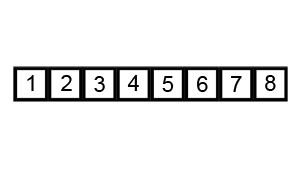
比较一下冒泡排序和简单选择排序的原理,我们不难发现:
在冒泡排序中, 第一个被排好了不再移动的对象位于序列的尾部;
在简单选择排序中,第一个被排好了不再移动的对象位于序列的首部。
o 冒泡排序(Bubble Sort)的C代码实现 : 函数bsort()
1 /* 2 * Bubble Sort (bsort in short) 3 */ 4 void bsort(int a[], size_t n) 5 { 6 for (int i = 0; i < n-1; i++) { // 1. i in [0, N-1), loop N-1 times 7 for (int j = 0; j < n-1-i; j++) { // 2. j in [0, N-1-i), 8 // walk unsorted list in per loop 9 if (a[j+1] < a[j]) { // 3. swap(j+1, j), 10 #define swap(m, n) do { int t = m; m = n; n = t; } while (0) 11 swap(a[j+1], a[j]); // compare every adjacent pair, 12 // swap their position if they 13 } // are not in the right order 14 } 15 } 16 }
接下来,给出一个完整的bsort.c并编译后测试, 以便形象化地理解冒泡排序的全过程。
o bsort.c // 将bsort()做稍稍增强以打印详细的排序过程。 注意:下面的程序中某些代码行风格很不好是故意的,因为只是为了帮助打印排序过程故一切从简。
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 typedef struct obs_s { 5 unsigned int loop; 6 unsigned int swap; 7 } obs_t; 8 9 obs_t g_obs = { .loop = 0, .swap = 0 }; 10 11 static void show(int a[], size_t n); 12 13 void bsort(int a[], size_t n) 14 { 15 for (int i = 0; i < n-1; i++) { 16 for (int j = 0; j < n-1-i; j++) { g_obs.loop++; 17 printf("#i=%d, j=%d: ", i, j); show(a, n); 18 if (a[j+1] < a[j]) { g_obs.swap++; 19 printf(" <-- swap(a[%d], a[%d])", j + 1, j); 20 #define swap(m, n) 21 do { int t = m; m = n; n = t; } while (0) 22 swap(a[j+1], a[j]); 23 } 24 printf(" "); 25 } 26 } 27 } 28 29 static void show(int a[], size_t n) 30 { 31 for (int i = 0; i < n; i++) 32 printf("%c ", a[i]); 33 } 34 35 int main(int argc, char *argv[]) 36 { 37 if (argc < 2) { 38 fprintf(stderr, "Usage %s <C1> [C2] ... ", argv[0]); 39 return -1; 40 } 41 42 argc--; 43 argv++; 44 45 size_t n = argc; 46 int *a = (int *)malloc(sizeof(int) * argc); 47 if (a == NULL) { 48 fprintf(stderr, "failed to malloc() "); 49 return -1; 50 } 51 52 for (int i = 0; i < n; i++) 53 *(a+i) = argv[i][0]; 54 55 printf(" 0 1 2 3 4 5 6 7 8 9 10 "); 56 printf("Before sorting: "); show(a, n); printf(" "); 57 bsort(a, n); 58 printf("After sorting: "); show(a, n); printf(" "); 59 printf(" "); 60 printf("Total loop times : %2d ", g_obs.loop); 61 printf("Total swap times : %2d ", g_obs.swap); 62 63 free(a); a = NULL; 64 return 0; 65 }
o 编译并测试
$ gcc -g -Wall -m32 -std=c99 -o bsort bsort.c $ ./bsort 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 9 10 Before sorting: 0 1 2 3 4 5 #i=0, j=0: 0 1 2 3 4 5 #i=0, j=1: 0 1 2 3 4 5 #i=0, j=2: 0 1 2 3 4 5 #i=0, j=3: 0 1 2 3 4 5 #i=0, j=4: 0 1 2 3 4 5 #i=1, j=0: 0 1 2 3 4 5 #i=1, j=1: 0 1 2 3 4 5 #i=1, j=2: 0 1 2 3 4 5 #i=1, j=3: 0 1 2 3 4 5 #i=2, j=0: 0 1 2 3 4 5 #i=2, j=1: 0 1 2 3 4 5 #i=2, j=2: 0 1 2 3 4 5 #i=3, j=0: 0 1 2 3 4 5 #i=3, j=1: 0 1 2 3 4 5 #i=4, j=0: 0 1 2 3 4 5 After sorting: 0 1 2 3 4 5 Total loop times : 15 Total swap times : 0 $ ./bsort 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 Before sorting: 5 4 3 2 1 0 #i=0, j=0: 5 4 3 2 1 0 <-- swap(a[1], a[0]) #i=0, j=1: 4 5 3 2 1 0 <-- swap(a[2], a[1]) #i=0, j=2: 4 3 5 2 1 0 <-- swap(a[3], a[2]) #i=0, j=3: 4 3 2 5 1 0 <-- swap(a[4], a[3]) #i=0, j=4: 4 3 2 1 5 0 <-- swap(a[5], a[4]) #i=1, j=0: 4 3 2 1 0 5 <-- swap(a[1], a[0]) #i=1, j=1: 3 4 2 1 0 5 <-- swap(a[2], a[1]) #i=1, j=2: 3 2 4 1 0 5 <-- swap(a[3], a[2]) #i=1, j=3: 3 2 1 4 0 5 <-- swap(a[4], a[3]) #i=2, j=0: 3 2 1 0 4 5 <-- swap(a[1], a[0]) #i=2, j=1: 2 3 1 0 4 5 <-- swap(a[2], a[1]) #i=2, j=2: 2 1 3 0 4 5 <-- swap(a[3], a[2]) #i=3, j=0: 2 1 0 3 4 5 <-- swap(a[1], a[0]) #i=3, j=1: 1 2 0 3 4 5 <-- swap(a[2], a[1]) #i=4, j=0: 1 0 2 3 4 5 <-- swap(a[1], a[0]) After sorting: 0 1 2 3 4 5 Total loop times : 15 Total swap times : 15 $ ./bsort S O R T E X A M P L E 0 1 2 3 4 5 6 7 8 9 10 Before sorting: S O R T E X A M P L E #i=0, j=0: S O R T E X A M P L E <-- swap(a[1], a[0]) #i=0, j=1: O S R T E X A M P L E <-- swap(a[2], a[1]) #i=0, j=2: O R S T E X A M P L E #i=0, j=3: O R S T E X A M P L E <-- swap(a[4], a[3]) #i=0, j=4: O R S E T X A M P L E #i=0, j=5: O R S E T X A M P L E <-- swap(a[6], a[5]) #i=0, j=6: O R S E T A X M P L E <-- swap(a[7], a[6]) #i=0, j=7: O R S E T A M X P L E <-- swap(a[8], a[7]) #i=0, j=8: O R S E T A M P X L E <-- swap(a[9], a[8]) #i=0, j=9: O R S E T A M P L X E <-- swap(a[10], a[9]) #i=1, j=0: O R S E T A M P L E X #i=1, j=1: O R S E T A M P L E X #i=1, j=2: O R S E T A M P L E X <-- swap(a[3], a[2]) #i=1, j=3: O R E S T A M P L E X #i=1, j=4: O R E S T A M P L E X <-- swap(a[5], a[4]) #i=1, j=5: O R E S A T M P L E X <-- swap(a[6], a[5]) #i=1, j=6: O R E S A M T P L E X <-- swap(a[7], a[6]) #i=1, j=7: O R E S A M P T L E X <-- swap(a[8], a[7]) #i=1, j=8: O R E S A M P L T E X <-- swap(a[9], a[8]) #i=2, j=0: O R E S A M P L E T X #i=2, j=1: O R E S A M P L E T X <-- swap(a[2], a[1]) #i=2, j=2: O E R S A M P L E T X #i=2, j=3: O E R S A M P L E T X <-- swap(a[4], a[3]) #i=2, j=4: O E R A S M P L E T X <-- swap(a[5], a[4]) #i=2, j=5: O E R A M S P L E T X <-- swap(a[6], a[5]) #i=2, j=6: O E R A M P S L E T X <-- swap(a[7], a[6]) #i=2, j=7: O E R A M P L S E T X <-- swap(a[8], a[7]) #i=3, j=0: O E R A M P L E S T X <-- swap(a[1], a[0]) #i=3, j=1: E O R A M P L E S T X #i=3, j=2: E O R A M P L E S T X <-- swap(a[3], a[2]) #i=3, j=3: E O A R M P L E S T X <-- swap(a[4], a[3]) #i=3, j=4: E O A M R P L E S T X <-- swap(a[5], a[4]) #i=3, j=5: E O A M P R L E S T X <-- swap(a[6], a[5]) #i=3, j=6: E O A M P L R E S T X <-- swap(a[7], a[6]) #i=4, j=0: E O A M P L E R S T X #i=4, j=1: E O A M P L E R S T X <-- swap(a[2], a[1]) #i=4, j=2: E A O M P L E R S T X <-- swap(a[3], a[2]) #i=4, j=3: E A M O P L E R S T X #i=4, j=4: E A M O P L E R S T X <-- swap(a[5], a[4]) #i=4, j=5: E A M O L P E R S T X <-- swap(a[6], a[5]) #i=5, j=0: E A M O L E P R S T X <-- swap(a[1], a[0]) #i=5, j=1: A E M O L E P R S T X #i=5, j=2: A E M O L E P R S T X #i=5, j=3: A E M O L E P R S T X <-- swap(a[4], a[3]) #i=5, j=4: A E M L O E P R S T X <-- swap(a[5], a[4]) #i=6, j=0: A E M L E O P R S T X #i=6, j=1: A E M L E O P R S T X #i=6, j=2: A E M L E O P R S T X <-- swap(a[3], a[2]) #i=6, j=3: A E L M E O P R S T X <-- swap(a[4], a[3]) #i=7, j=0: A E L E M O P R S T X #i=7, j=1: A E L E M O P R S T X #i=7, j=2: A E L E M O P R S T X <-- swap(a[3], a[2]) #i=8, j=0: A E E L M O P R S T X #i=8, j=1: A E E L M O P R S T X #i=9, j=0: A E E L M O P R S T X After sorting: A E E L M O P R S T X Total loop times : 55 Total swap times : 36
小结: 冒泡排序是一种稳定的排序,其时间复杂度和空间复杂度是:
Worst-case performance O(n**2)
Best-case performance O(n)
Average performance O(n**2)
Worst-case space complexity O(1) auxiliary
到此为止,我们已经完全弄明白了冒泡排序的原理,然并卵,因为冒泡排序的核心部分是双层嵌套循环,时间复杂度很高(O(N**2))。而且,伟大的计算机科学家高德纳(Donald E. Knuth)先生也说了"冒泡排序除了它迷人的名字和导致了某些有趣的理论问题这一事实之外,似乎没有什么值得推荐的", 所以,在高德纳先生的学生Robert Sedgewick与Kevin Wayne合著的《Algorithms》 (Fourth Edition)一书中,根本就不讲冒泡排序。那么,有没有更好的交换排序算法呢?答案是肯定的,那就是快速排序。欲知快速排序有多快,且听下回分解。