今天在给儿子看笔记本上的照片的时候,偶然发现了2009年手绘的一张a+b+c的N次方展开图,故写下面的博客以记之,为年轻时代的我点个赞!
20年前的我,一个充满激情的且富有专注力的数学发烧友!
10年前的我,一个无知者无畏的好写代码的疯狂的程序员!
而现在的我,一个被生活荡平了棱角的但是依然坚持理想的程序员。
言归正传,众所周知,a+b的N次方展开满足杨辉三角形。例如:
(a + b) ** 0 = 1 | 1
(a + b) ** 1 = a + b | 1 1
(a + b) ** 2 = a^2 + 2ab + b^2 | 1 2 1
(a + b) ** 3 = a^3 + 3a^2b + 3ab^2 + b^3 | 1 3 3 1
(a + b) ** 4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 | 1 4 6 4 1
国外将杨辉三角形叫做帕斯卡三角形(Pascal's triangle)。 引用维基百科的gif图动态呈现如下:
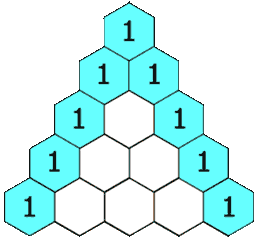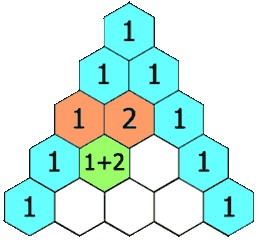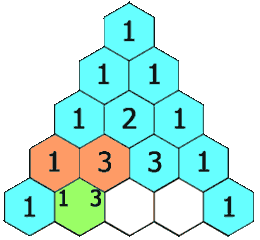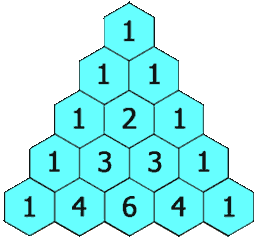
那么, a+b+c的N次方展开是什么样子滴? 高二(1997年的夏天)的时候(在学完二项式定理后),作为数学发烧友的我,硬是花了一个周末,废寝忘食地纯手工计算了N=0,1,2,3,4,5,6的情况,发现了如下图所示的规律。

注:上图为2009年我用Python实现了(a+b+c)**N后重绘的图片,那时候我已经是一个疯狂的程序员:-)
o abcN.py
1 #!/usr/bin/python 2 """ 3 A rough but simple solution to count expression 4 (a + b + c) ** n = ? 5 6 By Huanian<li.huanian@gmail.com> 7 On May, 2009 8 """ 9 10 import sys 11 12 def str2exp(s): 13 """ 14 1@a:2-b:1-c:1 => a^2bc 15 2@a:3-b:0-c:1 => 2a^3c 16 """ 17 i0, s0 = s.split('@') 18 sa, sb, sc = s0.split('-') 19 ca, ia = sa.split(':') 20 cb, ib = sb.split(':') 21 cc, ic = sc.split(':') 22 23 sout = "" 24 if i0 != '1': 25 sout += i0 26 if ia != '0': 27 if ia != '1': 28 s_ia = "%s^%s" % (ca, ia) 29 else: 30 s_ia = ca 31 sout += s_ia 32 if ib != '0': 33 if ib != '1': 34 s_ib = "%s^%s" % (cb, ib) 35 else: 36 s_ib = cb 37 sout += s_ib 38 if ic != '0': 39 if ic != '1': 40 s_ic = "%s^%s" % (cc, ic) 41 else: 42 s_ic = cc 43 sout += s_ic 44 return (sout) 45 46 def list2exp(lin): 47 lout = [] 48 for i in lin: 49 s = str2exp(i) 50 lout.append(s) 51 return (' + '.join(lout)) 52 53 def merge_list(lin): 54 """ 55 merge index of same entries 56 e.g. [1@a:1-b:2-c:0, 2@a:2-b:1:-c:0, 1@a:1-b:2-c:0] 57 ====> [2@a:1-b:2-c:0, 2@a:2-b:1:-c:0] 58 """ 59 ltmp = [] 60 for i in lin: 61 n, s = i.split('@') 62 if s not in ltmp: 63 ltmp.append(s) 64 65 lout = [] 66 for i in ltmp: 67 m = 0 68 for j in lin: 69 n, s = j.split('@') 70 if i == s: 71 m += int(n) 72 s = "%d@%s" % (m, i) 73 lout.append(s) 74 return (lout) 75 76 def exp_xx_1(lin): 77 """ list * ( a + b + c) """ 78 lout = [] 79 for i in lin: 80 n0, s0 = i.split('@') 81 sa, sb, sc = s0.split('-') 82 ca, ia = sa.split(':') 83 cb, ib = sb.split(':') 84 cc, ic = sc.split(':') 85 iia = int(ia) 86 iib = int(ib) 87 iic = int(ic) 88 for c in ['a', 'b', 'c']: 89 iia1 = iia 90 iib1 = iib 91 iic1 = iic 92 if c == ca: 93 iia1 += 1 94 elif c == cb: 95 iib1 += 1 96 elif c == cc: 97 iic1 += 1 98 else: 99 pass 100 s = "%s@a:%d-b:%d-c:%d" % (n0, iia1, iib1, iic1) 101 lout.append(s) 102 return (merge_list(lout)) 103 104 def exp_xx_n(lin, n): 105 if n == 0: 106 return ('1') 107 ltmp = lin 108 lout = ltmp 109 i = 1 110 while i < n: 111 lout = exp_xx_1(ltmp) 112 ltmp = lout 113 i += 1 114 s = list2exp(lout) 115 return (s) 116 117 def print2(s): 118 sys.stderr.write("%s " % s) 119 120 def main(argc, argv): 121 if argc != 2: 122 print2("Usage: %s <num>" % argv[0]) 123 print2("e.g. %s 1" % argv[0]) 124 print2(" (a + b + c) ** 1 = a + b + c") 125 return 1 126 127 imax = 64 # cost about 180s 128 n = int(argv[1]) 129 if n > imax: 130 print2("Your num=%d is too big, <= %d is better" % (n, imax)) 131 return 1 132 133 # string = "a + b + c" ==> list 134 l = ['1@a:1-b:0-c:0', '1@a:0-b:1-c:0', '1@a:0-b:0-c:1'] 135 # times it now... 136 s = exp_xx_n(l, n) 137 print "(a + b + c) ** %d = %s" % (n, s) 138 139 return (0) 140 141 if __name__ == '__main__': 142 argv = sys.argv 143 argc = len(argv) 144 sys.exit(main(argc, argv))
o 运行N=0..8
$ ./abcN.py 0 (a + b + c) ** 0 = 1 $ ./abcN.py 1 (a + b + c) ** 1 = a + b + c $ ./abcN.py 2 (a + b + c) ** 2 = a^2 + 2ab + 2ac + b^2 + 2bc + c^2 $ ./abcN.py 3 (a + b + c) ** 3 = a^3 + 3a^2b + 3a^2c + 3ab^2 + 6abc + 3ac^2 + b^3 + 3b^2c + 3bc^2 + c^3 $ ./abcN.py 4 (a + b + c) ** 4 = a^4 + 4a^3b + 4a^3c + 6a^2b^2 + 12a^2bc + 6a^2c^2 + 4ab^3 + 12ab^2c + 12abc^2 + 4ac^3 + b^4 + 4b^3c + 6b^2c^2 + 4bc^3 + c^4 $ ./abcN.py 5 (a + b + c) ** 5 = a^5 + 5a^4b + 5a^4c + 10a^3b^2 + 20a^3bc + 10a^3c^2 + 10a^2b^3 + 30a^2b^2c + 30a^2bc^2 + 10a^2c^3 + 5ab^4 + 20ab^3c + 30ab^2c^2 + 20abc^3 + 5ac^4 + b^5 + 5b^4c + 10b^3c^2 + 10b^2c^3 + 5bc^4 + c^5 $ ./abcN.py 6 (a + b + c) ** 6 = a^6 + 6a^5b + 6a^5c + 15a^4b^2 + 30a^4bc + 15a^4c^2 + 20a^3b^3 + 60a^3b^2c + 60a^3bc^2 + 20a^3c^3 + 15a^2b^4 + 60a^2b^3c + 90a^2b^2c^2 + 60a^2bc^3 + 15a^2c^4 + 6ab^5 + 30ab^4c + 60ab^3c^2 + 60ab^2c^3 + 30abc^4 + 6ac^5 + b^6 + 6b^5c + 15b^4c^2 + 20b^3c^3 + 15b^2c^4 + 6bc^5 + c^6 $ ./abcN.py 7 (a + b + c) ** 7 = a^7 + 7a^6b + 7a^6c + 21a^5b^2 + 42a^5bc + 21a^5c^2 + 35a^4b^3 + 105a^4b^2c + 105a^4bc^2 + 35a^4c^3 + 35a^3b^4 + 140a^3b^3c + 210a^3b^2c^2 + 140a^3bc^3 + 35a^3c^4 + 21a^2b^5 + 105a^2b^4c + 210a^2b^3c^2 + 210a^2b^2c^3 + 105a^2bc^4 + 21a^2c^5 + 7ab^6 + 42ab^5c + 105ab^4c^2 + 140ab^3c^3 + 105ab^2c^4 + 42abc^5 + 7ac^6 + b^7 + 7b^6c + 21b^5c^2 + 35b^4c^3 + 35b^3c^4 + 21b^2c^5 + 7bc^6 + c^7 $ ./abcN.py 8 (a + b + c) ** 8 = a^8 + 8a^7b + 8a^7c + 28a^6b^2 + 56a^6bc + 28a^6c^2 + 56a^5b^3 + 168a^5b^2c + 168a^5bc^2 + 56a^5c^3 + 70a^4b^4 + 280a^4b^3c + 420a^4b^2c^2 + 280a^4bc^3 + 70a^4c^4 + 56a^3b^5 + 280a^3b^4c + 560a^3b^3c^2 + 560a^3b^2c^3 + 280a^3bc^4 + 56a^3c^5 + 28a^2b^6 + 168a^2b^5c + 420a^2b^4c^2 + 560a^2b^3c^3 + 420a^2b^2c^4 + 168a^2bc^5 + 28a^2c^6 + 8ab^7 + 56ab^6c + 168ab^5c^2 + 280ab^4c^3 + 280ab^3c^4 + 168ab^2c^5 + 56abc^6 + 8ac^7 + b^8 + 8b^7c + 28b^6c^2 + 56b^5c^3 + 70b^4c^4 + 56b^3c^5 + 28b^2c^6 + 8bc^7 + c^8