数据压缩算法---霍夫曼编码的分析与实现

霍夫曼编码是一种基于最小冗余编码的压缩算法。最小冗余编码是指，如果知道一组数据中符号出现的频率，就可以用一种特殊的方式来表示符号从而减少数据需要的存储空间。一种方法是使用较少的位对出现频率高的符号编码，用较多的位对出现频率低的符号编码。我们要意识到，一个符号不一定必须是文本字符，它可以是任何大小的数据，但往往它只占一个字节。

熵和最小冗余

每个数据集都有一定的信息量，这就是所谓的熵。一组数据的熵是数据中每个符号熵的总和。符号z的熵S定义为：

S_z = -lg₂ P_z

其中，P_z就数据集中z出现的频率。来看一个例子，如果z在有32个符号的数据集中出现了8次，也就是1/4的概率，那么z的熵就是：

-lg ₂(1/4) = 2位

这意味着如果用超过两位的数来表示z将是一种浪费。如果在一般情况下用一个字节（即8位）来表示一个符号，那么在这种情况下使用压缩算法可以大幅减小数据的容量。

下表展示如何计算一个有72个数据实例熵的例子（其中有5个不同的符号）。要做到这一点，需将每个字符的熵相加。以U为例，它在数据集中出现了12次，所以每个U的实例的熵计算如下：

符号	概率	每个实例的熵	总的熵
U	12/72	2.584 963	31.019 55
V	18/72	2.000 000	36.000 00
W	7/72	3.362 570	23.537 99
X	15/72	2.263 034	33.945 52
Y	20/72	1.847 997	36.959 94

-lg₂(12/72) = 2.584 963 位

由于U在数据中出现了12次，因此整个数据的熵为：

2.584 963 * 12 = 31.019 55 位

为了计算数据集整体的熵，将每个字符所贡献的熵相加。每个字符的熵在表中已经计算出来了：

31.019 55 + 36.000 00 + 23.537 99 + 33.945 52 + 36.959 94 = 161.463 00 位

如果使用8位来表示每个符号，需要72 * 8 = 576位的空间，所以理论上来说，可以最多将此数据压缩：

1 - （161.463 000/576） = 72%

构造霍夫曼树

霍夫曼编码展现了一种基于熵的数据近似的最佳表现形式。它首先生成一个称为霍夫曼树的数据结构，霍夫曼树本身是一棵二叉树，用它来生成霍夫曼编码。霍夫曼编码是用来表示数据集合中符号的编码，用这种编码的方式达到数据压缩的目的。然而，霍夫曼编码的压缩结果往往只能接近于数据的熵，因为符号的熵往往是有小数位的，而在实际中，霍夫曼编码所用的位数不可能有小数位，所以有些代码会超过实际最优的代码位数。

 下图展示了用上表中的数据来构建一棵霍夫曼树的过程。构建的过程往往是从叶子结点向上进行。首先，将每个符号和频率放到它自身的树中（步骤1）。然后，将两个频率最小的根结点的树合并，并将其频率之和放到树的新结点中（步骤2）。这个过程反复持续下去，直到最后只剩下一棵树（这棵树就是霍夫曼树，步骤5）。霍夫曼的根结点包含数据中符号的总个数，它的叶子结点包含原始的符号和符号的频率。由于霍夫曼编码就是在不断寻找两棵最适合合并的树，因此它是贪婪算法的一个很好的例子。

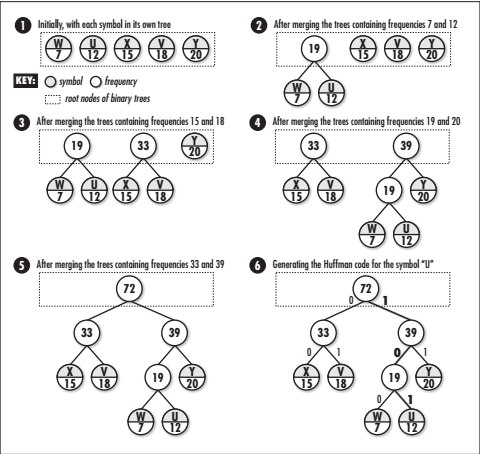
压缩和解压缩数据

建立一棵霍夫曼树是数据压缩和解压缩的一部分。

用霍夫曼树压缩数据，给定一个具体的符号，从树的根开始，然后沿着树的叶向叶子结点追踪。在向下追踪的过程中，当向左分支移动时，向当前编码的末尾追加0；当向右移动时，向当前编码的末尾追加1。在上图中，追踪“U”的霍夫曼编码，首先向右移动（1），然后向左移动（10），然后再向右（101）。图中符号的霍夫曼编码分别为：

U=101，V=01，W=100，X=00，Y=11

要解压缩用霍夫曼树编码的数据，要一位一位地读取压缩数据。从树的根开始，当在数据中遇到0时，向树的左分支移动；当遇到1时，向右分支移动。一旦到达一个叶子结点就找到了符号。接着从头开始，重复以上过程，直到所有的压缩数据都找出。用这种方法来解压缩数据是可能的，这是因为霍夫曼树是属于前缀树。前缀树是指一组代码中，任何一个编码都不是另一个编码的前缀。这就保证了编码被解码时不会有多义性。例如，“V”的编码是01，01不会是任何其他编码的前缀。因此，只要在压缩数据中碰到了01，就可以确定它表示的符号是“V”。

霍夫曼编码的效率

为了确定霍夫曼编码降低了多大容量的存储空间，首先要计算每个符号出现的次数与其编码位数的乘积，然后将其求和。所以，上表中压缩后的数据的大小为：

12*3 + 18*2 + 7*3 + 15*2 +20*2 = 163位

假设不使用压缩算法的72个字符均用8位表示，那么其总共所占的数据大小为576位，所以其压缩比计算如下：

1 - （163/576）=71.7%

再次强调的是，在实际中无法用小数来表示霍夫曼编码，所以在很多情况下这个压缩比并没有数据的熵效果那么好。但也非常接近于最佳压缩比。

在通常情况下，霍夫曼编码并不是最高效的压缩方法，但它压缩和解压缩的速度非常快。一般来说，造成霍夫曼编码比较耗时的原因是它需要扫描两次数据：一次用来计算频率；另一次才是用来压缩数据。而解压缩数据非常高效，因为解码每个符号的序列只需要扫描一次霍夫曼树。

霍夫曼编码的接口定义

huffman_compress

---

int huffman_compress(const unsigned char *original, unsigned char **compressed, int size);

返回值：如果数据压缩成功，返回压缩后数据的字节数；否则返回-1。

描述：用霍夫曼编码的方法压缩缓冲区original中的数据，original包含size字节的空间。压缩后的数据存入缓冲区compressed中。由于函数调用者并不知道compressed需要多大的空间，因此需要通过函数调用malloc来动态分配存储空间。当这块存储空间不再使用时，由调用者调用函数free来释放空间。

复杂度：O（n），其中n代表原始数据中符号的个数。

huffman_uncompress

---

int huffman_uncompress(const unsigned char *compressed, unsigned char **original);

返回值：如果解压缩成功，返回恢复后数据的字节数；否则返回-1。

描述：用霍夫曼的方法解压缩缓冲区compressed中的数据。假定缓冲区包含的数据是由Huffman_compress压缩产生的。恢复后的数据存入缓冲区original中。由于函数调用者并不知道original需要多大的空间，因此要通过函数调用malloc来动态分配存储空间。当这块存储空间不再使用时，由调用者调用free来释放空间。

复杂度：O（n），其中n是原始数据中符号的个数。

 霍夫曼编码的分析与实现

通过霍夫曼编码，在压缩过程中，我们将符号按照霍夫曼树进行编码从而压缩数据。在解压缩时，重建压缩过程中的霍夫曼树，同时将编码解码成符号本身。在本节介绍的实现过程中，一个原始符号都是用一个字节表示。

huffman_compress

huffman_compress操作使用霍夫曼编码来压缩数据。首先，它扫描数据，确定每个符号出现的频率。将频率存放到数组freqs中。完成对数据的扫描后，频率得到一定程度的缩放，因此它们可以只用一个字节来表示。当确定数据中某个符号的最大出现频率，并且相应确定其他频率后，这个扫描过程结束。由于数据中没有出现的符号，应该只是频率值为0的符号，所以执行一个简单的测试来确保当任何非0频率值其缩减为小于1时，最终应该将其值设为1而不是0。

一旦计算出了所有的频率，就调用函数build_tree来建立霍夫曼树。此函数首先将数据中至少出现过一次的符号插入优先队列中（实际上是一棵二叉树）。树中的结点由数据结构HuffNode定义。此结构包含两个成员：symbol为数据中的符号（仅在叶子结点中使用）；freq为频率。每棵树初始状态下只包含一个结点，此结点存储一个符号和它的缩放频率（就像在数据freqs中记录和缩放的一样）。

要建立霍夫曼树，通过优先队列用一个循环对树做size-1次合并。在每次迭代过程中，两次调用pqueue_extract来提取根结点频率最小的两棵二叉树。然后，将两棵树合并到一棵新树中，将两棵树的频率和存放到新树的根结点中，接着把新的树保存回优先级队列中。这个过程会一直持续下去，直到size-1次迭代完成，此时优先级队列中只有一棵二叉树，这就是霍夫曼树。

利用上一步建立的霍夫曼树，调用函数build_table来建立一个霍夫曼编码表，此表指明每个符号的编码。表中每个条目都是一个HuffCode结构。此结构包含3个成员：used是一个默认为1的标志位，它指示此条目是否已经存放一个代码；code是存放在条目中的霍夫曼编码；size是编码包含的位数。每个编码都是一个短整数，因为可以证明当所有的频率调整到可以用一个字节来表示时，没有编码会大于16位。

使用一个有序的遍历方法来遍历霍夫曼树，从而构建这个表。在每次执行build_table的过程中，code 记录当前生成的编码，size保存编码的位数。在遍历树时，每当选择左分支时，将0追加到编码的末尾中；每当选择右分支时，将1追加到编码的末尾中。一旦到达一个叶子结点，就将霍夫曼编码存放到编码表合适的条目中。在存放每个编码的同时，调用函数htons，以确保编码是以大端字节格式存放。这一步非常重要，因为在下一步生成压缩数据时需要用大端格式，同样在解压缩过程中也需要大端格式。

在产生压缩数据的同时，使用ipos来保存原始数据中正在处理的当前字节，并用opos来保存向压缩数据缓冲区写入的当前位。首先，缩写一个头文件，这有助于在huffman_uncompress中重建霍夫曼树。这个头文件包含一个四字节的值，表示待编码的符号个数，后面跟着的是所有256个可能的符号出现的缩放频率，也包括0。最后对数据编码，一次读取一个符号，在表中查找到它的霍夫曼编码，并将每个编码存放到压缩缓冲区中。在压缩缓冲区中为每个字节分配空间。

huffman_compress的时间复杂度为O（n），其中n是原始数据中符号的数量。

huffman_uncompress

huffman_uncompress操作解压缩由huffman_compress压缩的数据。首先，此操作读取追加到压缩数据的头。回想一下，头的前4个字节包含编码符号的数量。这个值存放在size中。接下来的256个字节包含所有符号的缩放频率。

利用存放在头中的信息，调用build_tree重建压缩过程中用到的霍夫曼树。一旦重建了树，接下来就要生成已恢复数据的缓冲区。要做到这一点，从压缩数据中逐位读取数据。从霍夫曼树的根开始，只要遇到位数0，就选择左分支；只要遇到位数1，就选择右分支。一旦到达叶子结点，就获取一个符号的霍夫曼编码。解码符号存储在叶子中。所以， 将此符号写入已恢复数据的缓冲区中。写入数据之后，重新回到根部，然后重复以上过程。使用ipos来保存向压缩数据缓冲区写入的当前位，并用opos来保存写入恢复缓冲区中的当前字节。一旦opos到达size，就从原始数据中生成了所有的符号。

huffman_uncompress的时间复杂度为O(n)。其中n是原始数据中符号的数量。这是因为对每个要解码符号来说，在霍夫曼树中向下寻找的深度是一个有界常量，这个常量依赖于数据中不同符号的数量。在本节的实现中，这个常量是256.建立霍夫曼树的过程不影响huffman_uncompress的复杂度，因为这个过程只依赖于数据中不同符号的个数。

 示例：霍夫曼编码的实现文件

/*huffman.c*/
#include <limit.h>
#include <netinet/in.h>
#include <stdlib.h>
#include <string.h>

#include "bit.h"
#include "bitree.h"
#include "compress.h"
#include "pqueue.h"

/*compare_freq 比较树中霍夫曼节点的频率*/
static int compare_freq(const void *tree1,const void *tree2)
{
    HuffNode *root1,root2;

    /*比较两棵二叉树根结点中所存储的频率大小*/
    root1 = (HuffNode *)bitree_data(bitree_root((const BiTree *)tree1));
    root2 = (HuffNode *)bitree_data(bitree_root((const BiTree *)tree2));

    if(root1->freq < root2->freq)
        return 1;
    else if(root1->freq > root2->freq)
        return -1;
    else return 0;
}
/*destroy_tree  消毁二叉树*/
static void destroy_tree(void *tree)
{
    /*从优先级队列中消毁并释放一棵二叉树*/
    bitree_destroy(tree);
    free(tree);

    return;
}
/*buile_tree 构建霍夫曼树，每棵树初始只包含一个根结点*/
static int bulid_tree(int *freqs,BiTree **tree)
{
    BiTree *init,
           *merge,
           *left,
           *right;
    PQueue pqueue;
    HuffNode *data;
    int size,c;

    /*初始化二叉树优先级队列*/
    *tree = NULL;
     pqueue_init(&pqueue,compare_freq,destroy_tree);
     for(c=0; c<=UCHAR_MAX; c++)
     {
         if(freqs[c] != 0)
         {
             /*建立当前字符及频率的二叉树*/
             if((init = (BiTree *)malloc(sizeof(BiTree))) == NULL)
             {
                 pqueue_destroy(&pqueue);
                 return -1;
             }

             bitree_init(init,free);
             if((data = (HuffNode*)malloc(sizeof(HuffNode))) == NULL)
             {
                 pqueue_destroy(&pqueue);
                 return -1;
             }

             data->symbol = c;
             data->freq = freqs[c];

             if(bitree_ins_left(init,NULL,data) != 0)
             {
                 free(data);
                 bitree_destroy(init);
                 free(init);
                 pqueue_destroy(&pqueue);
                 return -1;
             }

             /*将二叉树插入优先队列*/
             if(pqueue_insert(&pqueue,init) != 0)
             {
                 bitree_destroy(init);
                 free(init);
                 pqueue_destroy(&pqueue);
                 return -1;
             }
         }
     }
     /*通过两两合并优先队列中的二叉树来构建霍夫曼树*/
     for(c=1; c<=size-1; c++)
     {
         /*为合并后的树分配空间*/
         if((merge = (BiTree *)malloc(sizeof(BiTree))) == NULL)
         {
             pqueue_destroy(&pqueue);
             return -1;
         }

         /*提取队列中拥有最小频率的两棵树*/
         if(pqueue_extract(&pqueue,(void **)&left) != 0)
         {
             pqueue_destroy(&pqueue);
             free(merge);
             return -1;
         }
         if(pqueue_extract(&pqueue,(void **)right) !=0)
         {
             pqueue_destroy(&pqueue);
             free(merge);
             return -1;
         }
         /*分配新产生霍夫曼结点的空间*/
         if((data = (HuffNode *)malloc(sizeof(HuffNode))) == NULL)
         {
             pqueue_destroy(&pqueue);
             free(merge);
             return -1;
         }

         memset(data,0,sizeof(HuffNode));

         /*求和前面提取的两棵树的频率*/
         data->freq = ((HuffNode *)bitree_data(bitree_root(left)))->freq +
                      ((HuffNode *)bitree_data(bitree_root(right)))->freq;

        /*合并left、right两棵树*/
        if(bitree_merge(merge,left,right,data) != 0)
        {
            pqueue_destroy(&pqueue);
            free(merge);
            return -1;
        }

        /*把合并后的树插入到优先级队列中，并释放left、right棵树*/
        if(pqueue_insert(&pqueue,merge) != 0)
        {
            pqueue_destroy(&pqueue);
            bitree_destroy(merge);
            free(merge);
            return -1;
        }

        free(left);
        free(right);
     }

     /*优先队列中的最后一棵树即是霍夫曼树*/
     if(pqueue_extract(&pqueue,(void **)tree) != 0)
     {
         pqueue_destroy(&pqueue);
         return -1;
     }
     else
     {
         pqueue_destroy(&pqueue);
     }
     return 0;
}

/*build_table 建立霍夫曼编码表*/
static void build_table(BiTreeNode *node, unsigned short code, unsigned char size, HuffCode *table)
{
    if(!bitree_is_eob(node))
    {
        if(!bitree_is_eob(bitree_left(node)))
        {
            /*向左移动，并将0追加到当前代码中*/
            build_table(bitree_left(node),code<<1,size+1,table);
        }

        if(!bitree_is_eob(bitree_right(node)))
        {
            /*向右移动，并将1追加到当前代码中*/
            build_table(bitee_right(node),(code<<1) | 0x0001,size+1,table);
        }

        if(bitree_is_eob(bitree_left(node)) && bitree_is_eob(bitree_right(node)))
        {
            /*确保当前代码是大端格式*/
            code = htons(code);

            /*将当前代码分配给叶子结点中的符号*/
            table[((HuffNode *)bitree_data(node))->symbol].used = 1;
            table[((HuffNode *)bitree_data(node))->symbol].code = code;
            table[((HuffNode *)bitree_data(node))->symbol].size = size;
        }
    }
    return;
}
/*huffman_compress 霍夫曼压缩*/
int huffman_compress(const unsigned char *original, unsigned char **compressed, int size)
{
    BiTree        *tree;
    HuffCode      table[UCHAR_MAX + 1];
    int           freqs[UCHAR_MAX + 1],
                  max,
                  scale,
                  hsize,
                  ipos,opos,cpos,
                  c,i;
    unsigned      *comp,*temp;

    /*初始化，没有压缩数据的缓冲区*/
    *compressed = NULL;

    /*获取原始数据中每个符号的频率*/
    for(c=0; c <= UCHAR_MAX; c++)
        freqs[c] = 0;

    ipos = 0;

    if(size > 0)
    {
        while(ipos < size)
        {
            freqs[original[ipos]]++;
            ipos++;
        }
    }

    /*将频率缩放到一个字节*/
    max = UCHAR_MAX;

    for(c=0; c<=UCHAR_MAX; c++)
    {
        if(freqs[c] > max)
            max = freqs[c];
    }

    for(c=0; c <= UCHAR_MAX; c++)
    {
        scale = (int)(freqs[c] / ((double)max / (double)UCHAR_MAX));

        if(scale == 0 && freqs[c] != 0)
            freqs[c] = 1;
        else
            freqs[c] = scale;
    }

    /*建立霍夫曼树和编码表*/
    if(build_tree(freqs,&tree) != 0)
        return -1;

    for(c=0; c<=UCHAR_MAX; c++)
        memset(&table[c],0,sizeof(HuffCode));

    bulid_table(bitree_root(tree), 0x0000, 0, table);

    bitree_destroy(tree);
    free(tree);

    /*编写一个头代码*/
    hsize = sizeof(int) + (UNCHAR_MAX + 1);

    if((comp = (unsigned char *)malloc(hsize)) == NULL)
        return -1;

    memcpy(comp,&size,sizeof(int));

    for(c=0; c<=UCHAR_MAX; c++)
        comp[sizeof(int) + c] = (unsigned char)freqs[c];

    /*压缩数据*/
    ipos = 0;
    opos = hsize*8;

    while(ipos < size)
    {
        /*获取原始数据中的下一个字符*/
        c = original[ipos];

        /*将字符对应的编码写入压缩数据的缓存中*/
        for(i=0; i<table[c].size; i++)
        {
            if(opos % 8 == 0)
            {
                /*为压缩数据的缓存区分配另一个字节*/
                if((temp = (unsigned char *)realloc(comp,(opos/8)+1)) == NULL)
                {
                    free(comp);
                    return -1;
                }
                comp = temp;
            }
            cpos = (sizeof(short)*8) - table[c].size + i;
            bit_set(comp, opos, bit_get((unsigned char *)&table[c].code,cpos));
            opos++;
        }
        ipos++;
    }
    /*指向压缩数据的缓冲区*/
    *compressed = comp;

    /*返回压缩缓冲区中的字节数*/
    return ((opos - 1) / 8) + 1;
}

/*huffman_uncompress  解压缩霍夫曼数据*/
int huffman_uncompress(const unsigned char *compressed, unsigned char **original)
{
    BiTree      *tree;
    BiTreeNode  *node;
    int          freqs[UCHAR_MAX + 1],
                 hsize,
                 size,
                 ipos,opos,
                 state,
                 c;
    unsigned char *orig,*temp;
    
    /*初始化*/
    *original = orig = NULL;
    
    /*从压缩数据缓冲区中获取头文件信息*/
    hize = sizeof(int) + (UCHAR_MAX + 1);
    memcpy(&size,compressed,sizeof(int));
    
    for(c=0; c<=UCHAR_MAX; c++)
        freqs[c] = compressed[sizeof(int) + c];
    
    /*重建前面压缩数据时的霍夫曼树*/
    if(bulid_tree(freqs,&tree) != 0)
        return -1;
    
    /*解压缩数据*/
    ipos = hsize * 8;
    opos = 0;
    node = bitree_root(tree);
    
    while(opos < size)
    {
        /*从压缩数据中获取位状态*/
        state = bit_get(compressed,ipos);
        ipos++;
        
        if(state == 0)
        {
            /*向左移动*/
            if(bitree_is_eob(node) || bitree_is_eob(bitree_left(node)))
            {
                bitree_destroy(tree);
                free(tree);
                return -1;
            }
            else node = bitree_left(node);
        }
        else 
        {
            /*向右移动*/
            if(bitree_is_eob(node) || bitree_is_eob(bitree_right(node)))
            {
                bitree_destroy(tree);
                free(tree);
                return -1;
            }
            else node = bitree_right(node);
        }
        
        if(bitree_is_eob(bitree_left(node)) && bitree_is_eob(bitree_right(node)))
        {
            /*将叶子结点中的符号写入原始数据缓冲区*/
            if(opos > 0)
            {
                if((temp = (unsigned char *)realloc(orig,opos+1)) == NULL)
                {
                    bitree_destroy(tree);
                    free(tree);
                    free(orig);
                    return -1;
                }
                orig = temp;
            }
            else 
            {
                if((orig = (unsigned char *)malloc(1)) == NULL)
                {
                    bitree_destroy(tree);
                    free(tree);
                    return -1;
                }
            }
            
            orig[opos] = ((HuffNode *)bitree_data(node))->symbol;
            opos++;
            
            /*返回到霍夫曼树的顶部*/
            node = bitree_root(tree);
        }
    }
    bitree_destroy(tree);
    free(tree);
    
    /*把向原始数据缓冲区*/
    *original = orig;
    
    /*返回原始数据中的字节数*/
    return opos;
}