图是一种灵活的数据结构,它多用于描述对象之间的关系和连接模型。
关于图的算法:最小生成树、最短路径、旅行商问题以及许多其他算法大都会使用到广度优先搜索和深度优先搜索,因为它们提供了一套系统地访问图数据结构的方法。
带权图,是指图的每条边上带有一个值或权,这些权用一个小的数字标记在边上。很多条件因素都可以作为权值,但通常它表示遍历这条边所产生的代价。
最小生成树简述
我们做一个简单的模型,在一块木板上钉上一些钉子并用一些细绳连接起来,假设每一个钉子都经由一根或多根细绳连接起来。现在我们一根一根拿走细绳,直到用最少的细绳将所有钉子连接起来。这个模型的背后思想就是最小生成树。
正式的表述法是,给定一个无方向的带权图G=(V,E),最小生成树为集合T,T是以最小代价连接V中所有顶点所用边E的最小集合。集合T中的边能形成一颗树,这是因为每个顶点都能向上找到它的一个父节点(根结点除外)。
Prim算法
Prim算法是一种产生最小生成树的方法。
Prim算法从任意一个顶点开始,每次选择一个与当前顶点最近的一个顶点,并将两个顶点之间的边加入到树中。
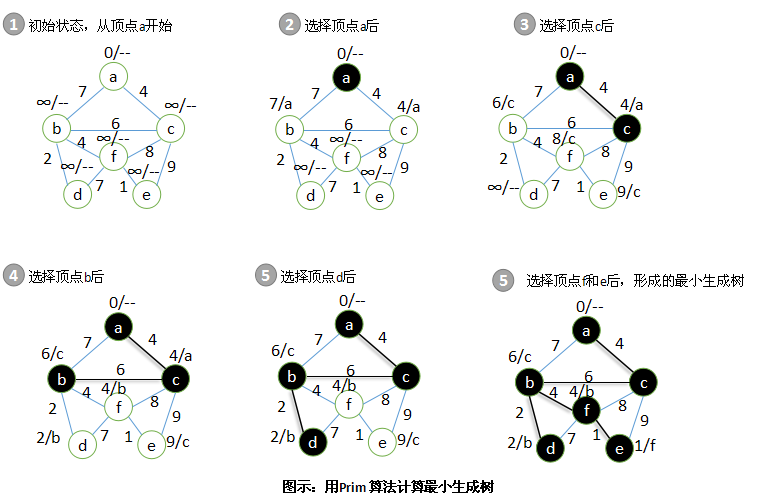
从根本上讲,Prim算法就是不断的选择顶点,并计算边的权值,同时判断是否还有更有效的连接方式。该算法类似广度优先搜索算法,因为在往图中更深的顶点探索之前,它首先要遍历与此顶点相关的所有顶点。每个阶段都要决定选择哪个顶点,所以需要维护顶点的颜色和键值。
开始,将所有顶点的色值设置为白色,键值设置为∞(它代表一个足够大的数,大于图中所有边的权值)。同时,将起始顶点的键值设置为0。随着算法的不断演进,在最小生成树中为每个顶点(除起始顶点外)指派一个父节点。只有当顶点的色值变为黑色时,此顶点才是最小生成树的一部分。
Prim算法的运行过程如下:
首先,在图中所有的白色顶点中,选择键值最小的顶点u。开始,键值被设置为0的那一顶点将作为起始顶点。
当选择此顶点之后,将其标记为黑色。
接下来,对于每个与u相邻的顶点v,设置v的键值为边(u,v)的权值,同时将u设置为v的父结点。
重复这个过程,直到所有的顶点都标记为黑色。
随着最小生成树的增长,该树会包含图中的所有的边(连接所有顶点最少数量边),且每条边的两端都有一个黑色的顶点。
下图展示了最小生成树的产生过程。在图中,键值和父结点都显示在每个顶点的旁边,用斜线分开。键值显示在斜线的左边,父结点显示在斜线的右边。浅灰色的边是最小生成树增长过程中的边。图中最小生成树总的权值为17。
最小生成树的接口定义
mst
int mst(Graph *graph, const MstVertex *start, List *span, int (*match)(const void *key1, const void *key2));
返回值:如果计算最小生成树成功,返回0,否则返回-1。
描述:为一个无方向的带权图graph计算最小生成树。
最小生成树从顶点start开始。
此操作会改变graph,所以如果有必要,在调用此操作之前先对图进行备份。
graph中的每个顶点必须包含MstVertex类型的数据。通过设置MstVertex结构体中的成员weight的值来指定每个边的权值,weight的值由传入graph_ins_edge的参数data2决定。用MstVertex结构体的成员data来保存与顶点相关的数据。
graph的match函数(此函数在用graph_init对图进行初始化时调用)用来比较MstVertex结构体中的data成员。此函数与传入mst中的参数match相同。
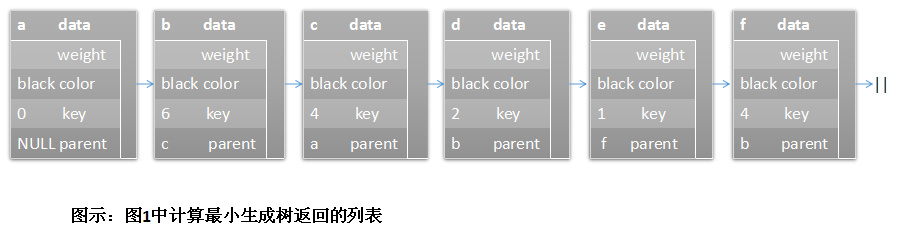
一旦计算完成,最小生成树的相关数据将会返回到span。span是存储MstVertex结构体的列表。在span中,父结点为NULL的顶点为最小生成树的根结点。其他每个顶点的parent成员都指向span中位于该顶点之前的那个顶点。
span中的顶点指向graph中的实际顶点,所以只要能够访问span,函数调用者就必须保证graph中内存空间有效。一旦不再使用span,就调用list_destroy销毁span。
复杂度:O(E V2),其中V是图中顶点的个数,E是边的条数。
最小生成树的实现与分析
为了计算一个无方向的带权图的最小生成树,首先,我们要用表示图的基本抽象数据类型来表示带权图。同时,Prim算法还需要一种追踪顶点和边信息的方法。这就用到了MstVertex结构体:它用来为图中的顶点计算最小生成树。此结构包含5个成员:data是与顶点相关的数据;weight是到达该顶点的边的权值;color是顶点的颜色;key是顶点的键值;parent是最小生成树中顶点的父结点。
建立一个包含MstVertex结构体的图的过程几乎与建立一个包含其他类型的图的过程一样:要将一个顶点插入图中,调用graph_ins_vertex,并将MstVertex结构体传入data。类似地,要将一条边插入图中,调用函数graph_ins_edge,并将MstVertex结构体传入data1和data2。当插入一个顶点时,只设置MstVertex结构体的data成员。当插入一条边时,设置data1的data成员,data2的data和weight成员。在data2中,weight是边的权值,此边是data1中的顶点到data2中顶点的连接线。在实际中,权值通常用浮点数进行存储和计算。由于键值是由权值计算来的,因此键值也用浮点数表示。
mst操作首先初始化邻接表结构链表中的每个顶点。将每个顶点的键值初始化为DBL_MAX(除超始顶点外,超始顶点初始值为0.0)。在图的抽象数据类型中,图由一个邻接表结构链表来表示。每个邻接表包含一个顶点和一个相邻顶点的集合。用存储在邻接表结构中的顶点来维护顶点的色值、键值、和父结点。维护邻接表结构链表中信息的关键是能将这些信息存储起来,而不是仅仅列出与自己相邻的顶点。鉴于一个顶点可能会出现在众多的邻接表中,所以每个顶点只能在邻接表结构链表中出现一次。
Prim算法的核心是用一个单循环为图中的每个结点迭代一次。在每次迭代的过程中:
首先,在所有的白色顶点中选择键值最小的顶点。同时,在邻接表结构链表把此顶点涂黑。
接下来,遍历与所选顶点相邻的顶点。在遍历每个顶点时,检查它在邻接表结构链表中的颜色和键值。一旦获取了这些信息,就将它与所选顶点的颜色和键值进行比较。如果相邻顶点是白色,且其键值比所选顶点的小,就将所选顶点与相邻顶点之间边的权值设置为相邻顶点的键值;同时,将相邻顶点的父结点设置为所选顶点。
然后,更新存储在邻接表结构链表中相邻顶点的信息。
重复这个过程,直到所有顶点都涂黑。
一旦Prim算法中的主循环结束,最小生成树也就计算完成了。此时,将邻接表结构链表中的每个黑色MstVertex结构体插入到链表span中。在span中,父结点为NULL的顶点就是最小生成树的根结点。其他每个顶点的parent成员都指向span中位于该顶点之前的那个顶点。每个MstVertex结构体的成员weight并不经常使用,因为它只有在存储到邻接表中时才用的到。
下图显示了上面的示例图中计算最小生成树所返回的MstVertex结构体链表:
示例:图算法的头文件(含最小生成树、最短路径、旅行商问题三种实现所需函数定义的头文件)
/*graphalg.h*/ #ifndef GRAPHALG_H #define GRAPHALG_H #include "graph.h" #include "list.h" /*定义最小生成树中结点的数据结构*/ typedef struct MstVertex_ { void *data; double weight; VertexColor color; double kdy; struct MstVertex_ *parent; }MstVertex; /*定义最短路径中结点的数据结构*/ typedef struct PathVertex_ { void *data; double weight; VertexColor color; double d; struct PathVertex_ *parent; }PathVertex; /*定义旅行商问题中结点的数据结构*/ typedef struct TspVertex_ { void *data; double x,y; VertexColor color; }TspVertex; /*函数接口*/ int mst(Graph *graph, const MstVertex *start, List *span, int (*match)(const void *key1, const void *key2)); int shortest(Graph *graph, const PathVertex *start, List *paths, int(*match)(const void *key1, const void *key2)); int tsp(List *vertexs, const TspVertex *start, List *tour, int (match*)(const void *key1, const void *key2)); #endif // GRAPHALG_H
示例:计算最小生成树的实现
/*mst.c*/ #include <float.h> #include <stdlib.h> #include "graph.h" #include "list.h" /*mst 计算最小生成树函数*/ int mst(Graph *graph, const MstVertex *start, List *span, int (*match)(const void *key1, const void *key2)) { AdjList *adjlist; MstVertex *mst_vertex, *adj_vertex; ListElmt *element, *member; double minmum; int found,i; /*初始化图中的所有结点*/ found=0; for(element=list_head(&graph_adjlists(graph)); element!=NULL; element = list_next(element)) { mst_vertex = ((AdjList *)list_data(element))->vertex; if(match(mst_vertex,start)) { /*匹配到起始顶点,并对其初始化*/ mst_vertex->color = white; mst_vertex->key = 0; mst_vertex->parent = NULL; found = 1; } else { /*非起始顶点的初始化*/ mst_vertex->color = white; mst_vertex->key = DBL_MAX; mst_vertex->parent = NULL; } } /*未找到起始顶点,函数返回*/ if(!found ) return -1; /*运用Prim算法计算最小生成树*/ i=0; while(i<graph_vcount(graph)) { /*选择拥有最小键值的白色顶点*/ minimum = DBL_MAX; for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element)) { mst_vertex = ((AdjList *)list_data(element))->vertex; if(mst_vertex->color == white && mst_vertex->key < minmum) { minmum = mst_vertex->key; adjlist = list_data(element); } } /*将已选择的顶点涂成黑色*/ ((MstVertex *)adjlist->vertex)->color = black; /*遍历被选中顶点的所有邻接顶点*/ for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(member)) { adj_vertex = list_data(member); for(element = list_head(&graph_adjlists(graph)); element != NULL; elemet = list_next(element)) { mst_vertex = ((AdjList *)list_data(element))->vertex; if(match(mst_vertex,adj_vertex)) { /*决定是否改变该顶点的键值或父结点*/ if(mst_vertex->color == white && adj_vertex->weight < mst_vertex->key) { mst_vertex->key = adj_vertex->weight; mst_vertex->parent = adjlist_vertex; } break; } } } /*准备选取下一个顶点*/ i++; } /*加载最小生成树到链表中*/ list_init(span,NULL); /*从邻接表结构链表中加载每个黑色结点*/ for(element = list_head(&graph_adjlists(graph)); elemet != NULL; element = list_next(element)) { /**/ mst_vertex = ((AdjList *)list_data(element))->vertex; if(mst_vertex->color == black) { if(list_ins_next(span, list_tail(span),mst_vertex) != 0) { list_destroy(span); return -1; } } } return 0; }