汇思学划水记

国庆汇思学笔记

DAY1

CRT

同余方程组
一般形式

[xequiv r1(mod m1)\ xequiv r2(mod m2)\ xequiv r3(mod m3)\ dots \ xequiv rn (mod mn) ]

证明
令(M=prod m_k)

[x=sum_{k=1}^n a_k imesfrac{M}{m_k}\ a_k imes frac{M}{m_k}equiv r_k (mod m_k)\ a_kequiv r_k imes frac{M}{m_k}^{-1}(mod m_k) ]

欧拉函数

(varphi(n))表示(1dots n)的与(n)互质的数
$varphi(n) = prod pi^{ci-1} imes(pi-1) $

/*线性晒素数->欧拉函数*/
for(int i=2;i<=n;i++){
	if(!notp[i]) pri[++cnt]=i,phi[i]=i-1;
	for(int j=1;j<=cnt;j++){
		if(i*pri[j]>n)break;
		notp[i*pri[j]]=1;
		if(i%pri[j]!=0) phi[i*pri[j]]=phi[i]*(pri[j]-1);
		if(i%pri[j]==0){
			phi[i*pri[j]]=phi[i]*pri[j];
			break;
		}
	}
}

组合数

公式

[C^{n}_m =frac{m!}{n!(m-n)!} ]

1. 卢卡斯定理

一个素数(p)，公式(C^m_n equiv C^{m mod p}_{n mod p} imes C^{lfloor m/p floor}_{lfloor n/p floor}pmod p)
相当于把(n)和(m)写成(k)进制((A_1 A_2 dots A_k),(B_1 B_2dots B_k))
那么

[C^m_n = prod_{i=1}^{k}C^{B_i}_{A_i} ]

2. 组合数有用的公式

1.(m imes C^m_n=n imes C^{m-1}_{n-1}) // 式子化简得来
2.(C^0_n+C^1_n+dots +C^n_n = 2^n)
3.(sum_{i=0}^{n}(-1)^i C^i_n =0) //奇数偶数和相等
4.(sum_{i=0}^{k}C^i_n imes C^{k-i}_m = C^k_{n+m})//常用来做突破口
5.二项式定理 ((a+b)^n =sum_{i=0}^{n}a^i b^{n-i}C^i_n)//形态极像杨辉三角

容斥原理

重要的功能化繁为简

斐波那契数列

例题待填坑

卡特兰数

公式

[C(1)=1\ C(n+1)=C(1)C(n)+C(2)C(n-1)+dots +C(n)(1) ]

卡特兰数通项公式

[C(n+1)=C(2n,n)-C(2n,n-1) ]

如何证明？折线法
向右为+1，向下为-1，所以我们一共为2n次，我们的目的是让它汇到(2n,0)点，所以一共有(C^n_2n)种方案，如果有不合法情况，那么意味着它会触碰(y=-1)这条直线。最终汇到(2n,-2)这个点，那么意味着有(n-1)种操作不合法

错排

推导公式
(D(n)=(n-1)[D(n-1)+D(n-2)])

高斯消元

意思是求一个方程组
慢慢的迭代即可

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define maxn 505
#define db double
#define eps 1e-8
using namespace std;

double a[maxn][maxn];

int n;

bool nos;

void gauss(){
	fo(i,1,n) {
		int wz=0;
		fo(j,i,n) {
			if (fabs(a[j][i])>eps) {
				wz=j;
				break;
			}
		}
		if (wz==0) {
			nos=1;
			return;
		}
		if (wz!=i) swap(a[i],a[wz]);
		db tmp=a[i][i];
		fo(j,1,n+1) a[i][j]/=tmp;
		fo(j,i+1,n) {
			db tmp=a[j][i];
			fo(k,1,n+1) a[j][k]-=a[i][k]*tmp;
		}
	}
	fd(i,n,1)
		fo(j,i+1,n) {
			if (fabs(a[i][j])>eps) a[i][n+1]-=a[j][n+1]*a[i][j],a[i][j]=0;
		}
}

int main(){
	cin>>n;
	fo(i,1,n)
		fo(j,1,n+1) cin>>a[i][j];
	gauss();
	if (nos) {
		puts("no solution");
	}
	else {
		fo(i,1,n) printf("%.8lf ",a[i][n+1]);
		puts("");
	}
	return 0;
}

感觉还是非常的神奇

至于今天的例题....本人到这已g

DAY2

概率和期望

性质：

1. 独立事件期望可以相加

2. 贝叶斯公式

[P(AB)=P(A) imes P(B | A)\ P(overline{A}B)=P(overline{A}) imes P(B | overline{A}) \ P(A | B)=frac{P(AB)}{P(B)} ]

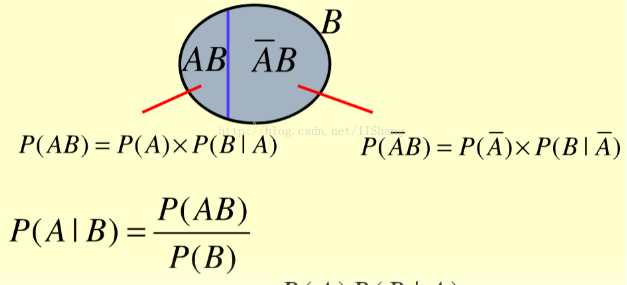
概率期望dp
一般分为两种形式

1. dp[i]表示i到达终点的期望，然后按照i逆推

2. dp[i]表示起点到i的期望，然后递推

例题：

本题就是给你一个飞行棋棋盘，投掷出每一个数字(1-6)的概率，问从起点开始到终点期望需要多少步？
最开始要投出6才可以起飞。
规则与传统飞行棋有一点不同。
投到6没有再来一次的机会

这道题有一个难点，就是每一点起飞时的期望步数。
答案是(frac{1}{p6})
为啥呢？
设(ans)等于期望步数，那么(Ans=p6+(1-p6)(Ans+1))，就可以求出
(ans=frac{1}{p6})
所以我们就可以设dp方程了

设状态0转移到1、2、3、……、n的费用都为1，各自概率为a、b、c、……，且和为1
再设状态x转移到终止态的期望为f(x)，
那么：f(0)=[f(1)a +f(2)b+f(3)*c+……]+1
我们求终点往回走的期望就好了

矩阵乘法

很简单

[C_{i,j}=sum_{k}A_{i,k} imes B_{k,j} ]

不满足交换律，满足结合律

例题：斐波那契数列第n项

模拟考试一

非常尴尬的一次考试，学OI第一次把文件名写错

T1求和

本来以为T1不会还可以打一个暴力，稳得40pts，结果开文件写错了文件格式，gg

本题求所有子段和的从大到小值
首先我的40pts枚举就好了
然后是正解做法。

首先开一个堆
你可以发现，如果当前子段([l,r])最大，那么([l-1,r])与([l,r+1])就已经用过了。
最大的子段是([1,n])
我们就可以枚举k次这样取最大值即可

种树

期望30，实际30

首先10分的数据是一棵树，20分的数据是只有一个环

然后考试的时候写40pts没写出来，大意是枚举每个点判断删去后能不能形成一棵树

正解的做法我只想出来了一部分，因为我想到了割点，但是我不知道怎么判断哪个不是割点的点可以删去。

后来经老师一讲就明白了，如果一个点删去，那么剩下的点构成一张图的话就需要n-2条边，所以判断一个点删去会不会删掉(m-(n-2))条边即可

自然数

这道题到目前还是很懵，并不知道怎么搞才好

可能目前只懂得50pts的做法，经仔细一想，感觉海星。
毕竟只有3000个数，所以我们存一下就好了，只要存小于3000的就可以。

正解二分线段树？？？
以下题解

对于 100%的数据
先用 50%的的方法 o(n),求出 mex(1,i).
可以知道 mex(i,i),mex(i,i+1)到 mex(i,n)是递增的。
然后使用线段树维护，需要不断删除前面的数。
比如删掉第一个数 a[1]. 那么在下一个 a[1]出现前的大于 a[1]
的 mex 值都要变成 a[1]
因为 mex 是单调递增的，所以找到第一个 mex>a[1]的位置，到
下一个 a[1]出现位置，这个区间的值变成 a[1].
然后需要线段树实现区间修改和区间求和。

还是很懵。

DAY3

七桥问题

贵族闲得慌，于是就让闲得慌的欧拉发明了闲得慌的数据结构-欧拉图

于是发现老师接着就跳过了七桥问题，达到了-什么是图...唔

于是证明了一些显而易见定理，虽然我稀里糊涂说了一大堆
定理如下：我就一口气写完了....

[1. sum depth(i)=sum size(i)\ 2. n个节点的二叉树高度至少为lfloor logn floor \ ]

唔，写到一半发现就这俩公式....那我们今天干啥了
哦，还有欧拉回路

欧拉回路

存在欧拉回路 等价于度为奇数的点有 0 个.
存在欧拉路径 等价于度为奇数的点有 0 或 2 个.
连通有向图 (边忽略方向后得到的无向图连通):
存在欧拉回路 等价于所有点出入度相等.
存在欧拉路径 等价于所有点出入度相等 或恰有一个点
入度比出度多 1 和恰有 1 个点出度比入度多 1

今天好像除了粘课件，没别的事可以干了吧...
等等，还有多源最短路

意思就是说，多个远点的最短路取最小值。
你可以建一个大的虚拟节点啊.....
然后将源点与它相连，跑最短路即可。

为什么我感觉dfs序的什么东西都没用啊？

DAY4

今天最有用的
就是

考了80竟然rank1
没关系。
关键是
我还只是会80分
bitset是个啥？为何T1还要用平方和？？
为何内存这么小？
为何出题人仍然谈笑风生？？

解题报告

小Ｔ的面试题

T1纠结中过了一个半小时，最后问老师才没跑偏题意

用了一个bool数组拿了30，最后发现要用到一个公式

[c=sum ai-sum^{n}_{i=1}i和d=frac{prod ai}{prod^{n}_{i=1}i} ]

然后解方程

[egin{cases} x-y=c\ xy^{-1}=d end{cases} ]

小Ｔ的绝对值

考试的时候一直在拼内存，本来可以40的结果一直缩小内存RE，开大数组后30

说一下50-60的步骤分，可以枚举右端点，然后二分左端点就可以了
还是没看懂最后的正解

每一个区间可以表示成两个前缀和的差.和的绝对值最小的两个区间在排序后必然相邻.对于大小相同的前缀和,需要求出其中最靠左和最靠右的一个

小T的递推式

一开始看数据范围，是能拿40分的，结果被全0的数据hack了，所以拿了30。
最后一道题的递推式是啊

[2^{n}a_0 mod (a_0+b_0) ]

然后坑点是可能等于0，所以需要特判0的情况。
突然发现还是可以的

DAY5

本以为今天会换老师，结果还是那个紧张的清华小哥

今天学习了动规.....
当然是弱智版的.....

线性dp

最大子段和问题

[dp[i]=max(dp[i-1]+a[i],a[i]) ]

最长上升子序列，有一个名词叫做LIS链
那么nlogn的求法正确性是啥呢？
因为有多条lis链，所以我们寻找的是最长的lis链来转移，这样可以维护最长

区间dp

[dp[l,r]=max(dp[l][k]+dp[k+1][r]+sum[r]-sum[l-1],\dp[l][r]) ]

基本就是这样，然后就是四边形不等式优化。你只要知道它转移的时候满足

[f_{l,r}+f_{l+1,r+1}le f_{l,r+1}+f_{l+1,r} ]

就可以了
至于证明，上课看推公式推到崩溃，看懂了但是不想码

环形dp

处理方法两种：

1. 将环倍长

2. 枚举一端点断环为链

环形最大子段和：
是用前缀和优化，emmm，然后单调队列维护一下。
环形LIS：
将相同的元素连起，形成不上升链。
环形最大独立集：
dp[i][0/1]表示当前点选或不选这样就可以破环为链

树形dp

树的直径：

1. 只有正边权：贪心，随便找到一个点最远的点，然后找到这个点另一个最远的点的距离，那么这就是树的直径

定理：一棵树上点最远的点是直径的一端

2. 负边权：dp，枚举每个点当做中转点，然后求出每个点的最大值+次大值，就是链长，然后ans维护一下，dp保留最大值

树上最远距离：
dp树的直径，加一个f数组，用来表示从上到下的最长距离。然后用个ans记录即可

树上最大独立集：
dp[u][0/1]就可以枚举求得