算法（第四版）C# 习题题解——3.1

写在前面

新增了一行内容。
整个项目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp
查找更方便的版本见：https://alg4.ikesnowy.com/
这一节内容可能会用到的库文件有 SymbolTable，同样在 Github 上可以找到。
善用 Ctrl + F 查找题目。

习题&题解

3.1.1

解答

官方解答：https://algs4.cs.princeton.edu/31elementary/GPA.java.html
ST.java：https://algs4.cs.princeton.edu/code/edu/princeton/cs/algs4/ST.java.html

建立一个符号表，然后把键值放进去，读取计算即可。
和上一章节用过的方法类似，先定义了一个接口 IST<Key, Value> ，包含书中提到的基本 API。
然后定义类 ST ，用标准库里面的 Dictionary 实现了 IST 。

代码

using System.Collections;
using System.Collections.Generic;

namespace SymbolTable
{
    /// <summary> 利用库函数实现的标准符号表。 </summary>
    public class ST<Key, Value> : IST<Key, Value>, IEnumerable<Key>
    {
        private Dictionary<Key, Value> st;

        /// <summary> 新建一个符号表。 </summary>
        public ST() => this.st = new Dictionary<Key, Value>();

        /// <summary> 检查符号表中是否存在与键 <paramref name="key"/> 对应的值。 </summary>
        public virtual bool Contains(Key key) => this.st.ContainsKey(key);

        /// <summary> 从符号表中删除键 <paramref name="key"/> 及对应的值。 </summary>
        public virtual void Delete(Key key) => this.st.Remove(key);

        /// <summary> 获取键 <paramref name="key"/> 对应的值，不存在时返回 null。 </summary>
        public virtual Value Get(Key key) => this.st[key];

        /// <summary> 获取枚举器。 </summary>
        public IEnumerator<Key> GetEnumerator() => this.st.Keys.GetEnumerator();

        /// <summary> 检查符号表是否为空。 </summary>
        public virtual bool IsEmpty() => this.st.Count == 0;

        /// <summary> 获得符号表中所有键的集合。 </summary>
        public virtual IEnumerable<Key> Keys() => this.st.Keys;

        /// <summary> 向符号表中插入新的键值对。 </summary>
        public virtual void Put(Key key, Value value) => this.st.Add(key, value);

        /// <summary> 获取符号表中键值对的数量。 </summary>
        public virtual int Size() => this.st.Count;

        /// <summary> 获取枚举器。 </summary>
        IEnumerator IEnumerable.GetEnumerator() => GetEnumerator();
    }
}

另请参阅

SymbolTable 库

3.1.2

解答

官方解答：https://algs4.cs.princeton.edu/31elementary/ArrayST.java.html

建立两个数组，分别存放键和值，一一对应。
添加时直接将新键值对放到数组最后即可。
删除时将待删除的键值对和位于最后的键值对交换，然后将其置空即可。

代码

using System;
using System.Collections.Generic;

namespace SymbolTable
{
    /// <summary>
    /// 符号表（数组实现）。
    /// </summary>
    /// <typeparam name="Key">键类型。</typeparam>
    /// <typeparam name="Value">值类型。</typeparam>
    public class ArrayST<Key, Value> : IST<Key, Value> 
    {
        private Key[] keys;             // 键数组
        private Value[] values;         // 值数组
        private int n = 0;              // 键值对数目

        /// <summary>
        /// 建立基于数组实现的符号表。
        /// </summary>
        public ArrayST() : this(8) { }

        /// <summary>
        /// 建立基于数组实现的符号表。
        /// </summary>
        /// <param name="initCapacity">初始大小。</param>
        public ArrayST(int initCapacity)
        {
            this.keys = new Key[initCapacity];
            this.values = new Value[initCapacity];
        }

        /// <summary>
        /// 检查键 <typeparamref name="Key"/> 是否存在。
        /// </summary>
        /// <param name="key">需要检查是否存在的键。</param>
        /// <returns></returns>
        public bool Contains(Key key) => Get(key).Equals(default(Key));

        /// <summary>
        /// 删除键 <paramref name="key"/> 及对应的值。
        /// </summary>
        /// <param name="key">需要删除的键。</param>
        public void Delete(Key key)
        {
            for (int i = 0; i < this.n; i++)
            {
                if (key.Equals(this.keys[i]))
                {
                    this.keys[i] = this.keys[this.n - 1];
                    this.values[i] = this.values[this.n - 1];
                    this.keys[this.n - 1] = default(Key);
                    this.values[this.n - 1] = default(Value);
                    this.n--;
                    if (this.n > 0 && this.n == this.keys.Length / 4)
                        Resize(this.keys.Length / 2);
                    return;
                }
            }
        }

        /// <summary>
        /// 获取键对应的值，若键不存在则返回 null。
        /// </summary>
        /// <param name="key">需要查找的键。</param>
        /// <returns></returns>
        public Value Get(Key key)
        {
            for (int i = 0; i < this.n; i++)
                if (this.keys[i].Equals(key))
                    return this.values[i];
            return default(Value);
        }

        /// <summary>
        /// 检查符号表是否为空。
        /// </summary>
        /// <returns></returns>
        public bool IsEmpty() => this.n == 0;

        /// <summary>
        /// 获得包含全部键的集合。
        /// </summary>
        /// <returns></returns>
        public IEnumerable<Key> Keys()
        {
            Key[] result = new Key[this.n];
            Array.Copy(this.keys, result, this.n);
            return result;
        }

        /// <summary>
        /// 向符号表中插入新元素，若键存在将被替换。
        /// </summary>
        /// <param name="key">键。</param>
        /// <param name="value">值。</param>
        public void Put(Key key, Value value)
        {
            Delete(key);

            if (this.n >= this.values.Length)
                Resize(this.n * 2);

            this.keys[this.n] = key;
            this.values[this.n] = value;
            this.n++;
        }

        /// <summary>
        /// 返回符号表中键值对的数量。
        /// </summary>
        /// <returns>键值对数量。</returns>
        public int Size() => this.n;

        /// <summary>
        /// 为符号表重新分配空间。
        /// </summary>
        /// <param name="capacity">新分配的空间大小。</param>
        private void Resize(int capacity)
        {
            Key[] tempKey = new Key[capacity];
            Value[] tempValue = new Value[capacity];

            for (int i = 0; i < this.n; i++)
                tempKey[i] = this.keys[i];
            for (int i = 0; i < this.n; i++)
                tempValue[i] = this.values[i];

            this.keys = tempKey;
            this.values = tempValue;
        }
    }
}

另请参阅

SymbolTable 库

3.1.3

解答

基于无序链表的官方实现：https://algs4.cs.princeton.edu/31elementary/SequentialSearchST.java.html

有序符号表的 API 见书中表 3.1.4（中文版 P230，英文版 P366）。
在官方实现的基础上修改 Put 方法，先找到合适位置再插入新的键值对，保证链表有序。
为方便插入操作，可以使用双向链表作为基础进行实现。
表中同时维护开头和末尾引用，加快获得最值的速度。

代码

using System;
using System.Collections.Generic;

namespace SymbolTable
{
    /// <summary>
    /// 基于有序链表的有序符号表实现。
    /// </summary>
    /// <typeparam name="Key">符号表键类型。</typeparam>
    /// <typeparam name="Value">符号表值类型。</typeparam>
    public class OrderedSequentialSearchST<Key, Value> : IST<Key, Value>, IOrderedST<Key, Value> 
        where Key : IComparable<Key>
    {
        /// <summary>
        /// 符号表结点。
        /// </summary>
        private class Node
        {
            public Key Key { get; set; }        // 键。
            public Value Value { get; set; }    // 值。
            public Node Next { get; set; }      // 后继。
            public Node Prev { get; set; }      // 前驱。
        }

        private Node first = null;      // 起始结点。
        private Node tail = null;       // 末尾结点。
        private int n = 0;              // 键值对数量。

        /// <summary>
        /// 构造基于有序链表的有序符号表。
        /// </summary>
        public OrderedSequentialSearchST() { }

        /// <summary>
        /// 大于等于 key 的最小值。
        /// </summary>
        /// <returns></returns>
        public Key Ceiling(Key key)
        {
            Node pointer = this.tail;
            while (pointer != null && Greater(key, pointer.Key))
                pointer = pointer.Prev;
            return pointer == null ? default(Key) : pointer.Key;
        }

        /// <summary>
        /// 键 <paramref name="key"/> 在表中是否存在对应的值。
        /// </summary>
        /// <param name="key">键。</param>
        /// <returns></returns>
        public bool Contains(Key key) => Floor(key).Equals(key);

        /// <summary>
        /// 从表中删去键 <paramref name="key"/> 对应的值。
        /// </summary>
        /// <param name="key">键。</param>
        public void Delete(Key key)
        {
            Node pointer = this.first;
            while (pointer != null && !pointer.Key.Equals(key))
                pointer = pointer.Next;
            if (pointer == null)
                return;
            Delete(pointer);
        }

        /// <summary>
        /// 从链表中删除结点 <paramref name="node"/>。
        /// </summary>
        /// <param name="node">待删除的结点。</param>
        private void Delete(Node node)
        {
            Node prev = node.Prev;
            Node next = node.Next;
            if (prev == null)
                this.first = next;
            else
                prev.Next = next;

            if (next == null)
                this.tail = prev;
            this.n--;
        }

        /// <summary>
        /// 删除最大的键。
        /// </summary>
        public void DeleteMax()
        {
            if (this.n == 0)
                throw new Exception("ST Underflow");
            Delete(this.tail);
        }

        /// <summary>
        /// 删除最小的键。
        /// </summary>
        public void DeleteMin()
        {
            if (this.n == 0)
                throw new Exception("ST Underflow");
            Delete(this.first);
        }

        /// <summary>
        /// 小于等于 Key 的最大值。
        /// </summary>
        /// <returns></returns>
        public Key Floor(Key key)
        {
            Node pointer = this.first;
            while (pointer != null && Less(key, pointer.Key))
                pointer = pointer.Next;
            return pointer == null ? default(Key) : pointer.Key;
        }

        /// <summary>
        /// 获取键 <paramref name="key"/> 对应的值，不存在则返回 null。
        /// </summary>
        /// <param name="key">键。</param>
        /// <returns></returns>
        public Value Get(Key key)
        {
            Node pointer = this.first;
            while (pointer != null && Greater(key, pointer.Key))
                pointer = pointer.Next;

            if (pointer == null)
                return default(Value);
            else if (pointer.Key.Equals(key))
                return pointer.Value;
            else
                return default(Value);
        }

        /// <summary>
        /// 符号表是否为空。
        /// </summary>
        /// <returns></returns>
        public bool IsEmpty() => this.n == 0;

        /// <summary>
        /// 获得符号表中所有键的集合。
        /// </summary>
        /// <returns></returns>
        public IEnumerable<Key> Keys() => this.n == 0 ? new List<Key>() : Keys(this.first.Key, this.tail.Key);

        /// <summary>
        /// 获得符号表中 [<paramref name="lo"/>, <paramref name="hi"/>] 之间的键。
        /// </summary>
        /// <param name="lo">范围起点。</param>
        /// <param name="hi">范围终点。</param>
        /// <returns></returns>
        public IEnumerable<Key> Keys(Key lo, Key hi)
        {
            List<Key> list = new List<Key>();
            Node pointer = this.first;
            while (pointer != null && Less(pointer.Key, lo))
                pointer = pointer.Next;
            while (pointer != null && Less(pointer.Key, hi))
            {
                list.Add(pointer.Key);
                pointer = pointer.Next;
            }
            if (pointer.Key.Equals(hi))
                list.Add(pointer.Key);
            return list;
        }

        /// <summary>
        /// 最大的键。
        /// </summary>
        /// <returns></returns>
        public Key Max() => this.tail == null ? default(Key) : this.tail.Key;

        /// <summary>
        /// 最小的键。
        /// </summary>
        /// <returns></returns>
        public Key Min() => this.first == null ? default(Key) : this.first.Key;

        /// <summary>
        /// 向符号表插入键值对，重复值将被替换。
        /// </summary>
        /// <param name="key">键。</param>
        /// <param name="value">值。</param>
        public void Put(Key key, Value value)
        {
            Delete(key);

            Node temp = new Node()
            {
                Key = key,
                Value = value,
                Prev = null,
                Next = null
            };

            Node left = null, right = this.first;
            while (right != null && Less(right.Key, temp.Key))
            {
                left = right;
                right = right.Next;
            }

            Insert(left, right, temp);

            if (left == null)
                this.first = temp;
            if (right == null)
                this.tail = temp;
            this.n++;
        }

        /// <summary>
        /// 小于 Key 的键的数量。
        /// </summary>
        /// <returns></returns>
        public int Rank(Key key)
        {
            int counter = 0;
            Node pointer = this.first;
            while (pointer != null && Less(pointer.Key, key))
            {
                pointer = pointer.Next;
                counter++;
            }
            return counter;
        }

        /// <summary>
        /// 获得排名为 k 的键（从 0 开始）。
        /// </summary>
        /// <param name="k">排名</param>
        /// <returns></returns>
        public Key Select(int k)
        {
            if (k >= this.n)
                throw new Exception("k must less than ST size!");

            Node pointer = this.first;
            for (int i = 0; i < k; i++)
                pointer = pointer.Next;
            return pointer.Key;
        }

        /// <summary>
        /// 获得符号表中键值对的数量。
        /// </summary>
        /// <returns></returns>
        public int Size() => this.n;

        /// <summary>
        /// [<paramref name="lo"/>, <paramref name="hi"/>] 之间键的数量。
        /// </summary>
        /// <param name="lo">范围起点。</param>
        /// <param name="hi">范围终点。</param>
        /// <returns></returns>
        public int Size(Key lo, Key hi)
        {
            int counter = 0;
            Node pointer = this.first;
            while (pointer != null && Less(pointer.Key, lo))
                pointer = pointer.Next;
            while (pointer != null && Less(pointer.Key, hi))
            {
                pointer = pointer.Next;
                counter++;
            }
            return counter;
        }

        /// <summary>
        /// 键 <paramref name="a"/> 是否小于 <paramref name="b"/>。
        /// </summary>
        /// <param name="a">检查是否较小的键。</param>
        /// <param name="b">检查是否较大的键。</param>
        /// <returns></returns>
        private bool Less(Key a, Key b) => a.CompareTo(b) < 0;

        /// <summary>
        /// 键 <paramref name="a"/> 是否大于 <paramref name="b"/>。
        /// </summary>
        /// <param name="a">检查是否较大的键。</param>
        /// <param name="b">检查是否较小的键。</param>
        /// <returns></returns>
        private bool Greater(Key a, Key b) => a.CompareTo(b) > 0;

        /// <summary>
        /// 将结点 <paramref name="k"/> 插入到 <paramref name="left"/> 和 <paramref name="right"/> 之间。
        /// </summary>
        /// <param name="left">作为前驱的结点。</param>
        /// <param name="right">作为后继的结点。</param>
        /// <param name="insert">待插入的结点。</param>
        private void Insert(Node left, Node right, Node k)
        {
            k.Prev = left;
            k.Next = right;
            if (left != null)
                left.Next = k;

            if (right != null)
                right.Prev = k;
        }
    }
}

另请参阅

SymbolTable 库

3.1.4

解答

利用 Time 类型记录时间，用 Event 来记录事件内容。

Time 类型包含时分秒三个 int 变量，同时实现 IComparable 接口。
Event 类型只包含事件的名称，相当于对 string 做了一个封装。

随后以 Time 为键类型，Event 为值类型，利用上一题编写的有序符号表进行操作。

代码

Time 类

using System;
using System.Text;

namespace _3._1._4
{
    /// <summary>
    /// 时间类。
    /// </summary>
    public class Time : IComparable<Time>
    {
        public int Hour { get; set; }
        public int Minute { get; set; }
        public int Second { get; set; }

        public Time() : this(0, 0, 0) { }

        public Time(int hour, int minute, int second)
        {
            this.Hour = hour;
            this.Minute = minute;
            this.Second = second;
        }

        public int CompareTo(Time other)
        {
            int result = this.Hour.CompareTo(other.Hour);
            if (result == 0)
                result = this.Minute.CompareTo(other.Minute);
            if (result == 0)
                result = this.Second.CompareTo(other.Second);
            return result;
        }

        public override bool Equals(object obj)
        {
            if (this == obj)
                return true;
            return CompareTo((Time)obj) == 0;
        }

        public override int GetHashCode()
        {
            int result = 1;
            result += this.Hour;
            result *= 31;
            result += this.Minute;
            result *= 31;
            result += this.Second;
            return result;
        }

        public override string ToString()
        {
            StringBuilder sb = new StringBuilder();
            sb.Append(this.Hour < 10 ? "0" + this.Hour : this.Hour.ToString());
            sb.Append(":");
            sb.Append(this.Minute < 10 ? "0" + this.Minute : this.Minute.ToString());
            sb.Append(":");
            sb.Append(this.Second < 10 ? "0" + this.Second : this.Second.ToString());
            return sb.ToString();
        }
    }
}

Event 类

namespace _3._1._4
{
    public class Event
    {
        public string EventMessage { get; set; }

        public Event() : this(null) { }

        public Event(string message)
        {
            this.EventMessage = message;
        }

        public override string ToString()
        {
            return this.EventMessage;
        }
    }
}

另请参阅

SymbolTable 库

3.1.5

解答

官方解答：https://algs4.cs.princeton.edu/31elementary/SequentialSearchST.java.html

size() 方法只需要直接返回当前的 n 值即可。
delete() 方法需要遍历链表，找到对应结点并删除。
keys() 方法只需要根据当前的 n 新建一个数组，把链表中的键值存入即可。

代码

/// <summary>
/// 从表中删去键 <paramref name="key"/> 及其对应的值。
/// </summary>
/// <param name="key">要删除的键。</param>
public void Delete(Key key)
{
    if (key == null)
        throw new ArgumentNullException("key can't be null");
    Node before = null, target = this.first;
    while (target != null && !target.Key.Equals(key))
    {
        before = target;
        target = target.Next;
    }
    if (target != null)
        Delete(before, target);
}

/// <summary>
/// 从链表中删除指定的结点。
/// </summary>
/// <param name="before"><paramref name="target"/> 的前驱。</param>
/// <param name="target">准备删除的结点。</param>
/// <exception cref="ArgumentNullException">当 <paramref name="target"/> 为 <c>null</c> 时抛出此异常。</exception>
private void Delete(Node before, Node target)
{
    if (target == null)
        throw new ArgumentNullException("target can't be null");

    if (before == null)
        this.first = target.Next;
    else
        before.Next = target.Next;
    this.n--;
}

/// <summary>
/// 获得所有的键。
/// </summary>
/// <returns>包含所有键的集合。</returns>
public IEnumerable<Key> Keys()
{
    Key[] keys = new Key[this.n];
    Node pointer = this.first;
    for (int i = 0; i < this.n; i++)
    {
        keys[i] = pointer.Key;
        pointer = pointer.Next;
    }
    return keys;
}

/// <summary>
/// 获取符号表中的键值对数量。
/// </summary>
/// <returns>当前符号表中的键值对数量。</returns>
public int Size() => this.n;

另请参阅

SymbolTable 库

3.1.6

解答

FrequencyCounter 的官方实现：https://algs4.cs.princeton.edu/31elementary/FrequencyCounter.java.html
每个单词都会被放进符号表一次，
因此 Put 的调用次数就等于单词总数 W +1（注意寻找最大值的时候有一次 Put 调用）
对于重复的单词，输入时会先调用 Get 获得当前计数之后再 Put 回去。
寻找最大值时，对于符号表中的每个键值都会调用两次 Get。
重复的单词数量 = (W - D)。
因此 Get 方法的调用次数 = (W - D) + 2D

3.1.7

解答

在 FrequencyCounter 中添加一个 CountDistinct 方法，计算不重复的键数。

public static int CountDistinct<TKey>(TKey[] keys, IST<TKey, int> st)
{
    int distinct = 0;
    for (int i = 0; i < keys.Length; i++)
    {
        if (!st.Contains(keys[i]))
            st.Put(keys[i], distinct++);
    }
    return distinct;
}

结果如下：

另请参阅

SymbolTable 库

3.1.8

解答

FrequencyCounter 的官方实现：https://algs4.cs.princeton.edu/31elementary/FrequencyCounter.java.html
《双城记》：https://introcs.cs.princeton.edu/java/data/tale.txt

官网给出的数据末尾有完整的版权说明，因此使用频率最高的单词变成了版权方的名字 Gutenberg-tm。
去掉末尾的版权声明之后，获得的单词是：Monseigneur

另请参阅

SymbolTable 库

3.1.9

解答

FrequencyCounter 的官方实现：https://algs4.cs.princeton.edu/31elementary/FrequencyCounter.java.html
《双城记》：https://introcs.cs.princeton.edu/java/data/tale.txt

对 FrequencyCounter 做修改，在调用 Put 方法之前，将单词记录在字符串变量 lastPut 中。
在读入单词结束之后输出 lastPut 和 words 变量。

将末尾的版权信息删除后，得到的结果如下：

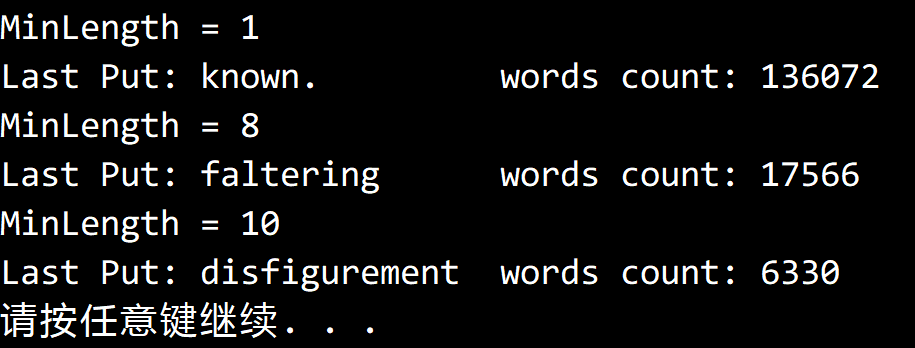
代码

public static string MostFrequentlyWord(string filename, int minLength, IST<string, int> st)
{
    int distinct = 0, words = 0;
    StreamReader sr = new StreamReader(File.OpenRead(filename));

    string[] inputs = 
        sr
        .ReadToEnd()
        .Split(new char[] { ' ', '
', '
' }, 
        StringSplitOptions.RemoveEmptyEntries);

    string lastPut = "";
    foreach (string s in inputs)
    {
        if (s.Length < minLength)
            continue;
        words++;
        if (st.Contains(s))
        {
            lastPut = s;
            st.Put(s, st.Get(s) + 1);
        }
        else
        {
            lastPut = s;
            st.Put(s, 1);
            distinct++;
        }
    }

    Console.WriteLine("Last Put: " + lastPut + "	 words count: " + words);

    string max = "";
    st.Put(max, 0);
    foreach (string s in st.Keys())
        if (st.Get(s) > st.Get(max))
            max = s;

    return max;
}

另请参阅

SymbolTable 库

3.1.10

解答

如图所示：

插入新的键值对需要遍历整个链表，比较次数等于链表在插入前的键值对数目。
修改已有的键值对则需要遍历链表直到找到该键值对，比较次数等于该键值对以及它之前所有键值对的数目。
共比较 0 + 1 + 2 + 3 + 4 + 5 + 6 + 4 + 6 + 7 + 8 + 9 = 55 次。

3.1.11

解答

键的轨迹如下图所示：

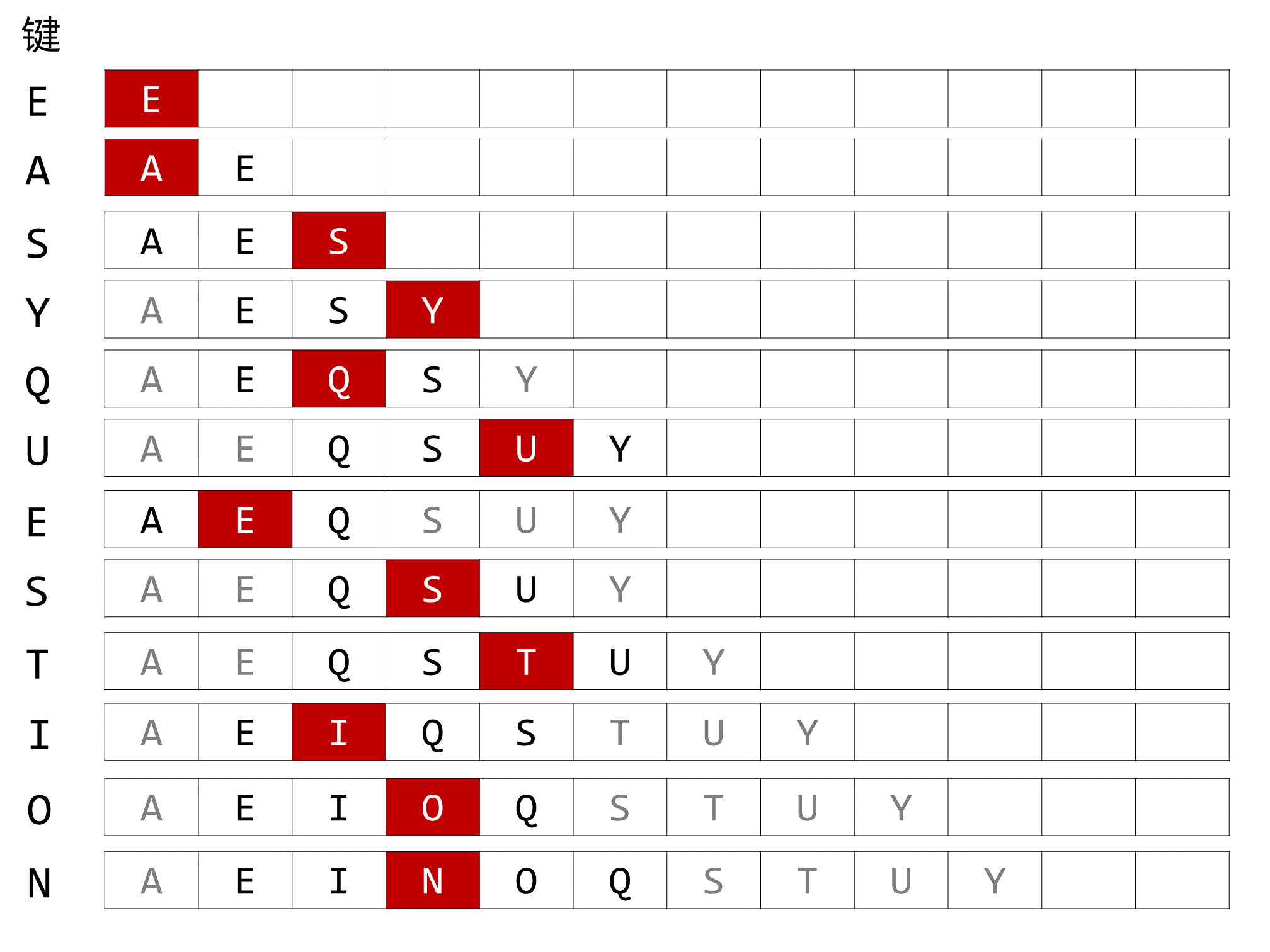
键查找使用二分查找优化，插入新的键时不必与每个键都进行比较。
共进行了 0 + 1 + 2 + 2 + 2 + 3 + 3 + 3 + 3 + 3 + 3 + 4 = 29 次比较。

3.1.12

解答

建立类 Item：

public class Item<TKey, TValue> : IComparable<Item<TKey, TValue>>
    where TKey : IComparable<TKey>
{
    public TKey Key { get; set; }
    public TValue Value { get; set; }

    public int CompareTo(Item<TKey, TValue> other)
    {
        return this.Key.CompareTo(other.Key);
    }
}

之后修改 BinarySearchST，将其中的 TKey[] keys 和 TValue[] values 数组用 Item[] items 数组代替。
例如 keys[i] 变为 items[i].Key，values[i] 变为 items[i].Value。

添加一个构造函数，调用之前编写的归并排序实现。

/// <summary>
/// 根据已有的键值对构造一个符号表。
/// </summary>
/// <param name="items">已有的键值对。</param>
public ItemBinarySearchST(Item<TKey, TValue>[] items)
{
    this.items = new Item<TKey, TValue>[items.Length];
    Array.Copy(items, this.items, items.Length);
    this.n = items.Length;
    MergeSort merge = new MergeSort();
    merge.Sort(this.items);
}

另请参阅

Merge 库
SymbolTable 库

3.1.13

解答

Get() 调用次数比 Put() 调用次数多了三个数量级，
BinarySearchST 和 SequentialSearchST 的平均 Put() 开销是一样的，
因此选择平均 Get() 开销更小的 BinarySearchST。

3.1.14

解答

根据上题给出的结论，选择 BinarySearchST。
由于 BinarySearchST 和 SequentialSearchST 执行 Put() 的开销相同
因此选择 Get() 开销更低的 BinarySearchST。

3.1.15

解答

假设先全部 Put()，再进行查找操作。
即分别进行 $ 1 $, $ 10 ^ 3 $, $ 10 ^ 6 $ 次插入
$ N = 1 $ 时，可以直接得出比例 $ 0.1 % (。 ) N = 10 ^ 3 $ 时，
插入耗时 $ = 1 + 2 + ... + 10 ^ 3 = 500500 $，
查询耗时 $ = 10 ^ 6 * lg(10 ^ 3) = 9965784 $，
比例为 $ 4.782 % (。 ) N = 10 ^ 6 $ 时
插入耗时 $ = 1 + 2 + ... + 10 ^ 6 = 500000500000 $，
查询耗时 $ = 10 ^ 9 * lg(10 ^ 6) = 19931568569 $，
比例为 $ 96.17 % ​$。

3.1.16

解答

官方实现：https://algs4.cs.princeton.edu/31elementary/BinarySearchST.java.html

先通过二分查找获得下标，然后后面的元素依次向前移动一位。

public void Delete(TKey key)
{
    if (key == null)
        throw new ArgumentNullException("argument to Delete() is null");
    if (IsEmpty())
        return;

    int i = Rank(key);

    if (i == this.n && this.keys[i].CompareTo(key) != 0)
        return;

    for (int j = i; j < this.n - 1; j++)
    {
        this.keys[j] = this.keys[j + 1];
        this.values[j] = this.values[j + 1];
    }

    this.n--;
    this.keys[this.n] = default(TKey);
    this.values[this.n] = default(TValue);

    if (this.n > 0 && this.n == this.keys.Length / 4)
        Resize(this.n / 2);
}

另请参阅

SymbolTable 库

3.1.17

解答

官方实现：https://algs4.cs.princeton.edu/31elementary/BinarySearchST.java.html

先通过二分查找大于等于 key 的键下标 i，
如果 keys[i] 和 key 相等则直接返回 keys[i]，
否则返回 keys[i-1]。

public TKey Floor(TKey key)
{
    if (key == null)
        throw new ArgumentNullException("argument to Floor() is null");
    int i = Rank(key);
    if (i < this.n && this.keys[i].CompareTo(key) == 0)
        return this.keys[i];
    if (i == 0)
        return default(TKey);
    else
        return this.keys[i - 1];
}

另请参阅

SymbolTable 库

3.1.18

解答

设 key 为目标键。
算法初始时 lo = 0, hi = n - 1，数组已排序。
当找到目标键时，返回的下标 mid 显然是正确的。
（0...a[mid - 1] 都小于 a[mid]，同时 a[mid] = key）

接下来证明：当目标键不存在时，lo 可以代表小于 key 的键的个数。
由算法内容，当循环退出时，一定有 lo 和 hi 交叉，即 lo > hi。
考虑最后一次循环，必然执行了 lo = mid + 1 或者 hi = mid - 1。
即最后一次循环之后 lo = mid + 1 > hi 或 hi = mid - 1 < lo。
又由于 mid = (lo + hi) / 2，代入有：
即(lo + hi) / 2 + 1 > hi 或(lo + hi) / 2 - 1 < lo
(lo - hi) / 2 + 1 > 0 或(hi - lo) / 2 - 1 < 0
(hi - lo) / 2 < 1
hi - lo < 2
由于 hi 和 lo 都是整数，故有 hi -lo <= 1

由算法的内容可以得出，最后一次循环时，
下标小于 lo 的元素都小于 key，下标大于 hi 的元素都大于 key
且下标小于 lo 的元素正好有 lo 个 （0...lo - 1)。

当 lo = hi 时，mid = lo
若 key > lo，则 lo = lo + 1，即 a[lo] 本身也小于 key。
若 key < lo，lo 不变，即 a[lo] 就是大于 key 的第一个元素。

当 lo = hi - 1 时，mid = lo
若 key > lo，则 lo = lo + 1 = hi，变为上一种情况。
若 key < lo，则 hi = lo - 1，a[lo] 是大于 key 的第一个元素。

综上，Rank() 是正确的。

3.1.19

解答

将频率和当前最大频率相同的单词都放到一个队列里即可。

string max = "";
Queue<string> queue = new Queue<string>();
st.Put(max, 0);
foreach (string s in st.Keys())
{
    if (st.Get(s) > st.Get(max))
    {
        max = s;
        queue.Clear();
        queue.Enqueue(s);
    }
    else if (st.Get(s) == st.Get(max))
    {
        queue.Enqueue(s);
    }
}

另请参阅

SymbolTable 库

3.1.20

解答

国内的书中关于命题 B 的证明有错误，新版的证明如下：

虽然新版还是有个小错误，$ n-2 $ 应该改为 $ k-2 $。
勘误见：https://algs4.cs.princeton.edu/errata/errata-printing11.php。

先证单调性，利用数学归纳法：
已知对于 $ N=0 ​$，满足 $ C(0) le C(1) ​$。
假设对于 $ N=n ​$，满足 $ C(n) le C(n+1) ​$。
根据递归式，有：

[egin{eqnarray*} & C(n) & le C(lfloor n/2 floor) + 1 \ \ & C(n+1) & le egin{cases} C(lfloor n/2 floor) +1 & ext{$ n $ 是偶数} \ C(lfloor n/2 floor + 1) + 1 & ext{$ n $ 是奇数} end{cases}\ \ & C(n+2) & le C(lfloor n/2 floor + 1) + 1 end{eqnarray*} ]

又 $ C(n) le C(n+1) ​$ ，推出 $ C(lfloor n/2 floor) + 1 le C(lfloor n/2 floor + 1) + 1 ​$。
故 $ C(n+1) le C(n+2) ​(，由数学归纳法，) C(n) le C(n+1) ​$ 成立。

已知当 $ N = 2^k - 1 $ 时，有 $ C(N) le k = lg(N+1) le lg N + 1$。
接下来证明在 $ (2^k - 1, 2^{k + 1} -1) $ 范围内上式仍然成立。
不妨设 $ 0 < M < 2^k $ ，则有 $ 2^k - 1 < N + M < 2^{k + 1} -1 (。 转变为证：) C(N+M) le lg (N+M) + 1 $ 。
由于 $ C(N+M) $ 是一个整数，则 $ lfloor lg(N+M) +1 floor = k+1 $。
即求证： $ C(N+M) le k+1 $。
由单调性可得 $ C(N+M) le C(2^{k+1} - 1) le k+1 ​$，得证。

3.1.21

解答

BinarySearchST
包含一个键数组和一个值数组，以及一个 int 变量。
数组长度变化范围为 N~4N ，故总大小：
从 2 × (24 + 8N) +4 = 52 + 16N 字节 （100 %），
到 2 × (24 + 32N) +4 = 52 + 64N 字节（25 %）之间变动。
SequentialSearchST
包含 N 个结点以及一个 int 变量
(16 + 8 + 8 + 8)N + 4 = 4 + 40N 字节

3.1.22

解答

对 Get() 做修改，得到 MoveToFrontArrayST。

public TValue Get(TKey key)
{
    int i;
    for (i = 0; i < this.n; i++)
        if (this.keys[i].Equals(key))
            break;

    if (i == this.n)
        return default(TValue);

    TKey toFrontKey = this.keys[i];
    TValue toFrontValue = this.values[i];

    for (int j = i; j > 0; j--)
        this.keys[j] = this.keys[j - 1];
    for (int j = i; j > 0; j--)
        this.values[j] = this.values[j - 1];

    this.keys[0] = toFrontKey;
    this.values[0] = toFrontValue;

    return this.values[0];
}

另请参阅

SymbolTable 库

3.1.23

解答

这里的右移操作可以理解为 「小数点前移一位」
即数字依次向右退一位，个位上的数字被舍弃。
对于十进制，小数点前移一位会使 $ n $ 变为 $ lfloor n / 10 floor $。
同样对于二进制就会使 $ n $ 变为 $ lfloor n / 2 floor $。
当需要除以 $ 2 $ 的 $ k $ 次幂的时候，可以用右移 $ k $ 位代替并减少时间开销。
同理可以用左移 $ k $ 位来代替乘以 $ 2 $ 的 $ k $ 次幂。
注：
这样会降低程序可读性，
并且某些语言（C / C++）的编译器已经可以自动执行这项优化了。
请充分考虑你的代码受众之后再决定是否采用这种写法。

二分查找的最大查找次数 = $ lg N + 1$ （见 3.1.20 的证明）
一个数最多被左移的次数也正好等于 $ lfloor lg N floor + 1 $
（任意正整数都能被表示为 $ 2 ^ k + m $ 的形式，即 $ k +1 $ 位二进制数）
因此一次二分查找所需的最大比较次数正好是 $ N $ 的二进制表示的位数。

3.1.24

解答

FrequencyCounter 的官方实现：https://algs4.cs.princeton.edu/31elementary/FrequencyCounter.java.html

二分查找总是与中间值进行比较，现在改为与数组中第 x% 位置上的元素比较。
具体而言，$ frac{k_x-k_{lo}}{k_{hi}-k_{lo}} $ 代表数组在均匀情况下目标值 $ k_x $ 的相对位置（一个比率，在数组第 x% 的位置上）。
那么相对应的下标就等于 $ lo+frac{k_x-k_{lo}}{k_{hi}-k_{lo}} imes (hi - lo) $。
用这个式子代替原来的 $ mid=lo + (hi-lo)/2 $ 即可。

不难看出这种方法对于分布相对均匀的数组比较有利，相对于二分查找而言迭代次数会少很多。
但如果数组分布不够均匀，也可能表现出不如二分查找的性能。

实验结果也证实了这一判断，就随机数组而言，插值查找相对于二分查找只有 1% 左右的性能提升。

代码

SearchCompare 在书中没有出现，但可以简单的实现为调用 FrequencyCounter 并计时的方法：

public static long Time<TKey>(IST<TKey, int> st, TKey[] keys)
{
    Stopwatch sw = new Stopwatch();
    sw.Start();
    FrequencyCounter.MostFrequentlyKey(st, keys);
    sw.Stop();
    return sw.ElapsedMilliseconds;
}

由于这里需要使用数字而非字符串作为键值，需要对官方给出的 FrequencyCounter 做一些修改：

public static TKey MostFrequentlyKey<TKey> (IST<TKey, int> st, TKey[] keys)
{
    foreach (TKey s in keys)
    {
        if (st.Contains(s))
            st.Put(s, st.Get(s) + 1);
        else
            st.Put(s, 1);
    }

    TKey max = keys[0];
    foreach (TKey s in st.Keys())
        if (st.Get(s) > st.Get(max))
            max = s;

    return max;
}

另请参阅

SymbolTable 库

3.1.25

解答

英文原文指的是 most recently accessed key，因此指的是最近访问的键。

实现比较简单，先在类中定义一个新的成员 cache 作为缓存，
然后修改 Get 方法，在实际查找之前先检查缓存，如果缓存未命中则在查找之后更新它。
要注意的是缓存指向内容的有效性，在数组中指的是下标是否有效，在链表中指的是结点是否为空。

利用《双城记》测试的结果：

代码

BinarySearchST

cache 是一个 int 类型的变量，代表下标。
在二分查找前先检查缓存，要注意cache超出数组大小的情况。
如果缓存未命中，则进行二分查找，并在返回结果前更新缓存。

public TValue Get(TKey key)
{
    if (key == null)
        throw new ArgumentNullException("argument to Get() is null");
    if (IsEmpty())
        return default(TValue);
    if (this.cache < this.n && this.keys[this.cache].Equals(key)) // 缓存检查
        return this.values[this.cache];
    int rank = Rank(key);
    if (rank < this.n && this.keys[rank].Equals(key))
    {
        this.cache = rank;                                        // 更新缓存
        return this.values[rank];
    }

    return default(TValue);
}

SequentialSearchST

cache 是一个结点类型的变量，代表一个键值对。
类似的，在顺序查找前先检查缓存，如果缓存未命中则更新缓存。
要注意的是如果缓存的结点被删除，需要将缓存置为 null。

Get() 方法

public TValue Get(TKey key)
{
    if (key == null)
        throw new ArgumentNullException("key can't be null");

    if (this.cache != null && this.cache.Key.Equals(key)) // 检查缓存
        return this.cache.Value;
    for (Node pointer = this.first; pointer != null; pointer = pointer.Next)
    {
        if (pointer.Key.Equals(key))
        {
            this.cache = pointer;                         // 更新缓存
            return pointer.Value;
        }
    }
    return default(TValue);
}

Delete() 方法

public void Delete(TKey key)
{
    if (key == null)
        throw new ArgumentNullException("key can't be null");
    Node before = null, target = this.first;
    while (target != null && !target.Key.Equals(key))
    {
        before = target;
        target = target.Next;
    }
    if (target == this.cache)           // 删除缓存
        this.cache = null;
    if (target != null)
        Delete(before, target);
}

另请参阅

SymbolTable 库

3.1.26

解答

字典文件：https://introcs.cs.princeton.edu/java/data/web2.txt
《双城记》：https://introcs.cs.princeton.edu/java/data/tale.txt
浏览器可能会直接打开 txt，此时右键链接-目标另存为即可下载。

FrequencyCounter 的官方实现：https://algs4.cs.princeton.edu/31elementary/FrequencyCounter.java.html

我们利用 BinarySearchST 会自动对键排序的性质来实现字典序排序。
首先将字典存到一个符号表中，按照 “单词-序号” 的形式保存。
然后读入文件，如果读入的单词存在于字典中，
则将其以 “序号-单词” 的形式存到 BinarySearchST 中去。
读入完毕后，遍历 BinarySearchST 即可获得字典序的单词列表。

对于按频率排序，我们基于已有的实现修改。
在每次取得最大值之后，输出并删除最大值，如此循环即可获得频率排序的单词序列。
也可以将单词-频率序列全部读出来存放到数组之中，然后用第二章的排序算法排序。

测试结果，取 minLength = 13，只截取了部分。

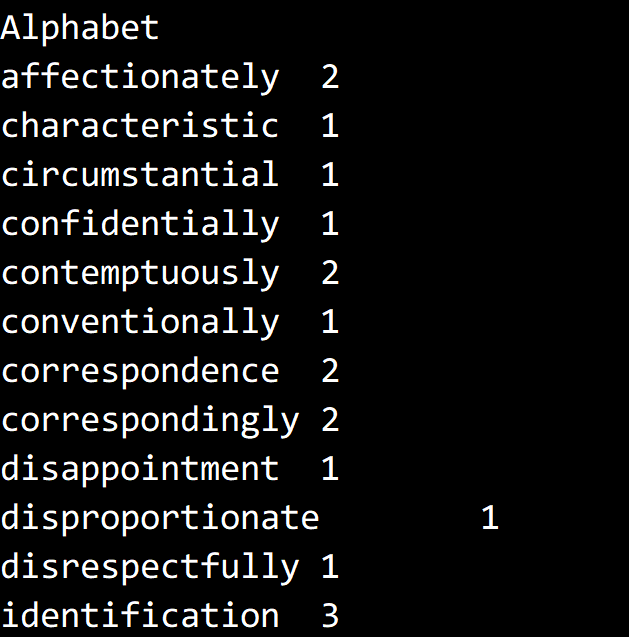
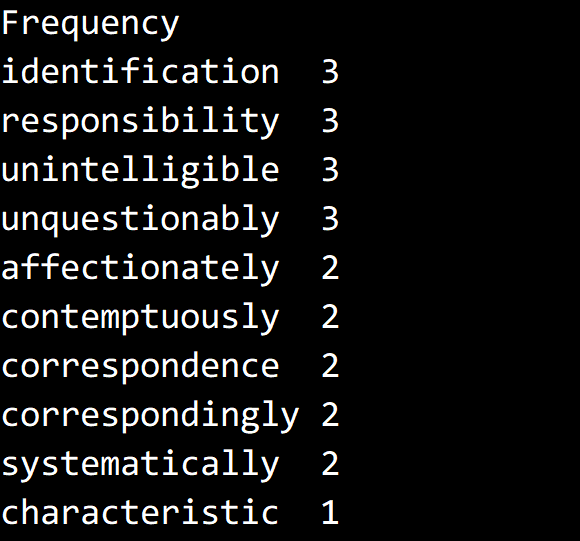
代码

public static void LookUpDictionary(string filename, string dictionaryFile, int minLength)
{
    // 初始化字典
    StreamReader sr = new StreamReader(File.OpenRead(dictionaryFile));
    string[] words = sr.ReadToEnd().Split(new char[] { ' ', '
', '
' }, StringSplitOptions.RemoveEmptyEntries);
    BinarySearchST<string, int> dictionary = new BinarySearchST<string, int>();
    for (int i = 0; i < words.Length; i++)
    {
        if (words[i].Length > minLength)
            dictionary.Put(words[i], i);
    }
    sr.Close();

    // 读入单词
    StreamReader srFile = new StreamReader(File.OpenRead(filename));
    string[] inputs = srFile.ReadToEnd().Split(new char[] { ' ', '
', '
' }, StringSplitOptions.RemoveEmptyEntries);
    srFile.Close();

    BinarySearchST<int, string> stDictionary = new BinarySearchST<int, string>();
    BinarySearchST<string, int> stFrequency = new BinarySearchST<string, int>();
    foreach (string s in inputs)
    {
        if (stFrequency.Contains(s))
            stFrequency.Put(s, stFrequency.Get(s) + 1);
        else if (dictionary.Contains(s))
        {
            stFrequency.Put(s, 1);
            stDictionary.Put(dictionary.Get(s), s);
        }
    }

    // 输出字典序
    Console.WriteLine("Alphabet");
    foreach (int i in stDictionary.Keys())
    {
        string s = stDictionary.Get(i);
        Console.WriteLine(s + "	" + stFrequency.Get(s));
    }

    // 频率序
    Console.WriteLine("Frequency");
    int n = stFrequency.Size();
    for (int i = 0; i < n; i++)
    {
        string max = "";
        stFrequency.Put(max, 0);
        foreach (string s in stFrequency.Keys())
            if (stFrequency.Get(s) > stFrequency.Get(max))
                max = s;
        Console.WriteLine(max + "	" + stFrequency.Get(max));
        stFrequency.Delete(max);
    }
}

另请参阅

SymbolTable 库

3.1.27

解答

事实上就是说，先构造一个包含 N 个不重复键的符号表，然后进行 S 次查找。
给出 S 的增长数量级，使得构造符号表的成本和查找的成本相同。

这里假设一次数组交换和一次比较的成本是相同的。
先考虑构造符号表的成本，一次 Put() 需要调用一次 Rank() 和一次插入操作。
2.1 节插入排序的命题 B 给出了每次插入平均需要移动一半的数组元素的结论。
于是构造符号表所需的成本约为：$nlg n + frac{1}{2}sum_{k=1}^{n} k=nlg n + frac{n(n-1)}{4} $ 。
这里查找的成本是这么计算的：$ lg0+lg1+cdots+lg n < nlg n $
查找所需的成本比较简单，一次二分查找的比较次数约为 $ lg n $，总成本就是 $ Slg n $ 。
令两边相等，解方程即可得到 $ S=n+frac{n(n-1)}{4lg n} $ 。

如果用大 O 记法，也可以记为 $ O(n^2 / lg n) $，如果要选择一个比较常用的上界则可以选择 $ O(n^2) $。

实验结果，两边的成本是很接近的：

另请参阅

SymbolTable 库

3.1.28

解答

将重新分配数组空间的代码提前，然后添加判断语句即可。
BinarySearchSTOrderedInsertion：

/* 省略 */

if (this.n == this.keys.Length)
    Resize(this.n * 2);

// 如果插入的键比所有键都大则直接插入末尾。
if (this.n == 0 || this.keys[this.n - 1].CompareTo(key) < 0)
{
    this.keys[this.n] = key;
    this.values[this.n] = value;
    this.n++;
    return;
}

int i = Rank(key);

/* 省略 */

另请参阅

SymbolTable 库

3.1.29

解答

官方实现：https://algs4.cs.princeton.edu/31elementary/TestBinarySearchST.java.html

官方实现中有几处错误，需要做一些修改。

/* 省略 */

Console.WriteLine("Testing Select()");
Console.WriteLine("-----------------------------------");
for (int i = 0; i < st.Size(); i++) // 循环条件不能有 '='
    Console.WriteLine(i + " " + st.Select(i));
Console.WriteLine();

/* 省略 */

while (!st.IsEmpty())
    st.Delete(st.Select(st.Size() / 2));
Console.WriteLine("After deleting the remaining keys");
Console.WriteLine("-----------------------------------");
// 异常处理
try
{
    foreach (string s in st.Keys())
        Console.WriteLine(s + " " + st.Get(s));
}
catch (Exception ex)
{
    Console.WriteLine("Exception: " + ex.Message);
}
Console.WriteLine();

/* 省略 */

结果如下：

size = 10
min = A
max = X

Testing Keys()
-----------------------------------
A 8
C 4
E 12
H 5
L 11
M 9
P 10
R 3
S 0
X 7

Testing Select()
-----------------------------------
0 A
1 C
2 E
3 H
4 L
5 M
6 P
7 R
8 S
9 X

key Rank Floor Ceil
-----------------------------------
A 0 A A
B 1 A C
C 1 C C
D 2 C E
E 2 E E
F 3 E H
G 3 E H
H 3 H H
I 4 H L
J 4 H L
K 4 H L
L 4 L L
M 5 M M
N 6 M P
O 6 M P
P 6 P P
Q 7 P R
R 7 R R
S 8 S S
T 9 S X
U 9 S X
V 9 S X
W 9 S X
X 9 X X
Y 10 X
Z 10 X

After deleting the smallest 3 keys
-----------------------------------
H 5
L 11
M 9
P 10
R 3
S 0
X 7

After deleting the remaining keys
-----------------------------------
Exception: called Min() with empty table

After adding back N keys
-----------------------------------
A 8
C 4
E 12
H 5
L 11
M 9
P 10
R 3
S 0
X 7

另请参阅

SymbolTable 库

3.1.30

解答

官方实现：https://algs4.cs.princeton.edu/31elementary/BinarySearchST.java.html。

首先在 BinarySearchST 中添加如下方法。

/// <summary> 检查符号表结构是否有效。 </summary>
private bool Check() => IsSorted() && RankCheck();

/// <summary> 检查 <see cref="keys"/> 数组是否有序。 </summary>
private bool IsSorted()
{
    for (int i = 1; i < Size(); i++)
        if (this.keys[i].CompareTo(this.keys[i - 1]) < 0)
            return false;
    return true;
}

/// <summary> 检查 Rank(Select(i)) = i 是否成立。 </summary>
private bool RankCheck()
{
    for (int i = 0; i < Size(); i++)
        if (i != Rank(Select(i)))
            return false;
    for (int i = 0; i < Size(); i++)
        if (keys[i].CompareTo(Select(Rank(this.keys[i]))) != 0)
            return false;
    return true;
}

然后在 Put() 和 Delete() 方法的末尾添加：Debug.Assert(Check()); 即可。

另请参阅

SymbolTable 库

3.1.31

解答

性能测试方法构造如下：
先编写一个随机字符串方法，生成一个长度大于 50 的字符串（作为未命中访问）。
然后随机生成符合要求的字符串数组，将它们全部放入符号表中。
然后遍历 10 次生成的字符串数组，对于数组中的每个元素都进行一次命中查询。
同时在每次命中查询的同时都进行一次未命中查询即可。

测试结果：

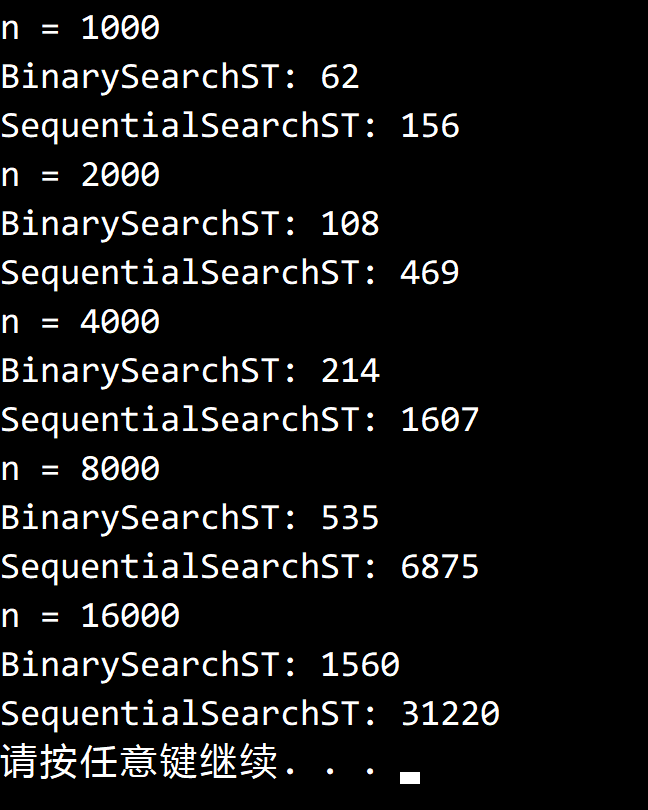
代码

按照要求编写代码，在 SearchCompare 类里添加一个 Random random 成员，并添加如下方法：
随机字符串发生器：

public static string GetRandomString(int minLength, int maxLength)
{
    int length = random.Next(minLength, maxLength);
    StringBuilder sb = new StringBuilder();
    for (int i = 0; i < length; i++)
    {
        double choice = random.NextDouble();
        if (choice < 0.333)
            sb.Append((char)random.Next('A', 'Z'));
        else if (choice < 0.666)
            sb.Append((char)random.Next('a', 'z'));
        else
            sb.Append((char)random.Next('0', '9'));
    }
    return sb.ToString();
}

生成随机字符串数组：

public static string[] GetRandomArrayString(int n, int minLength, int maxLength)
{
    string[] result = new string[n];
    for (int i = 0; i < n; i++)
    {
        result[i] = GetRandomString(minLength, maxLength);
    }
    return result;
}

测试方法：

public static long Performance(IST<string, int> st, int n, int averageHit)
{
    string[] keys = GetRandomArrayString(n, 2, 50);
    string keyNotExist = GetRandomString(51, 52);
    Stopwatch sw = Stopwatch.StartNew();
    // 构建
    for (int i = 0; i < n; i++)
        st.Put(keys[i], i);
    // 查询
    for (int i = 0; i < averageHit; i++)
    {
        for (int j = 0; j < n; j++)
        {
            st.Get(keys[j]);
            st.Get(keyNotExist);
        }
    }
    sw.Stop();
    return sw.ElapsedMilliseconds;
}

另请参阅

SymbolTable 库

3.1.32

解答

编码实现即可，实验结果如下：

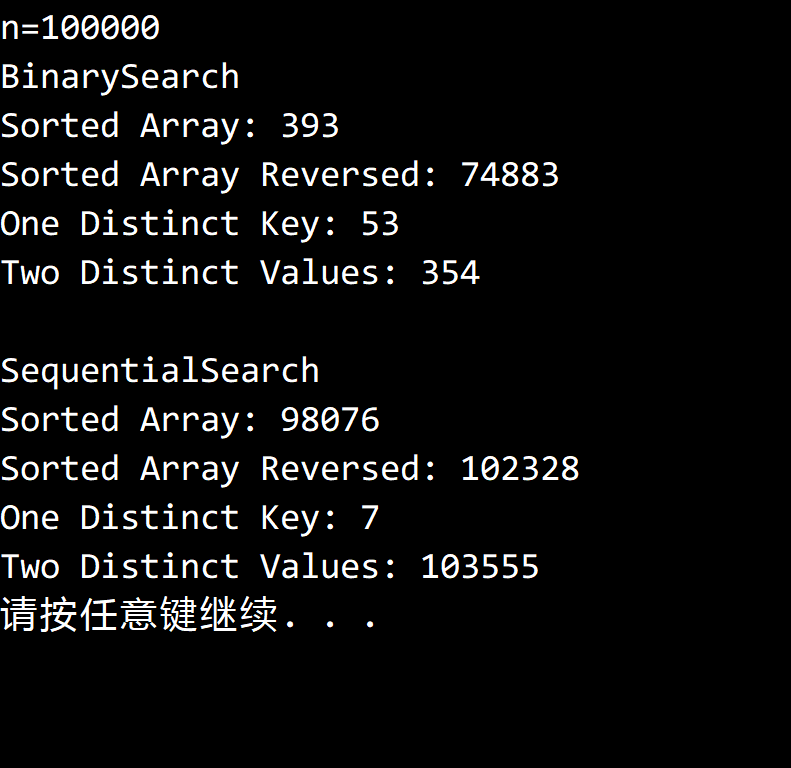
对于保持键有序的 BinarySearchST 来说，逆序输入是最坏情况，顺序输入则是最好情况。
而对于键无序的 SequentialSearchST 来说，输入顺序对于性能的影响不大。
只有一种键的时候，每次 Put 都只需要比较一次，值一直在被替换。
只有两种值对性能的影响不大，性能主要由输入的键决定。

代码

测试方法，IST 代表一个符号表。

static void Test(IST<string, int>[] sts, int n)
{
    Stopwatch sw = new Stopwatch();
    string[] data = SearchCompare.GetRandomArrayString(n, 3, 10);
    string item1 = "item1";
    Array.Sort(data);

    // 有序的数组
    Console.Write("Sorted Array: ");
    sw.Start();
    for (int i = 0; i < n; i++)
    {
        sts[0].Put(data[i], i);
    }
    sw.Stop();
    Console.WriteLine(sw.ElapsedMilliseconds);

    // 逆序的数组
    Console.Write("Sorted Array Reversed: ");
    sw.Restart();
    for (int i = n - 1; i >= 0; i--)
    {
        sts[1].Put(data[i], i);
    }
    sw.Stop();
    Console.WriteLine(sw.ElapsedMilliseconds);

    // 只有一种键
    Console.Write("One Distinct Key: ");
    sw.Restart();
    for (int i = 0; i < n; i++)
    {
        sts[2].Put(item1, i);
    }
    sw.Stop();
    Console.WriteLine(sw.ElapsedMilliseconds);

    // 只有两种值
    Console.Write("Two Distinct Values: ");
    sw.Restart();
    for (int i = 0; i < n; i++)
    {
        sts[3].Put(data[i], i % 2);
    }
    sw.Stop();
    Console.WriteLine(sw.ElapsedMilliseconds);
}

另请参阅

SymbolTable 库

3.1.33

解答

概率分布的实现方式：
假设存有键的数组为 keys，对 keys 排序。
然后再建立一个长度为 10N 的数组 querys，
前 1/2 置为 keys[0]，1/2 到 3/4 置为 keys[1]，以此类推，直到数组填满。
然后遍历 query 数组，对符号表进行 Get() 操作。

实验结果如下：

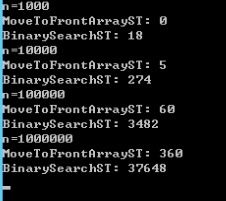
代码

static void Main(string[] args)
{
    int n = 1000;
    int multiplyBy10 = 3;
    for (int i = 0; i < multiplyBy10; i++)
    {
        Console.WriteLine("n=" + n);
        // 构造表
        BinarySearchST<string, int> bst = new BinarySearchST<string, int>(n);
        MoveToFrontArrayST<string, int> mst = new MoveToFrontArrayST<string, int>(n);
        string[] keys = SearchCompare.GetRandomArrayString(n, 3, 20);
        for (int j = 0; j < n; j++)
        {
            bst.Put(keys[j], j);
            mst.Put(keys[j], j);
        }
        // 构造查询
        Array.Sort(keys);
        string[] querys = new string[10 * n];
        int queryIndex = 0, keyIndex = 0;
        while (queryIndex < querys.Length)
        {
            int searchTimes = (int)Math.Ceiling((Math.Pow(0.5, keyIndex + 1) * querys.Length));
                    
            for (int j = 0; j < searchTimes && queryIndex < querys.Length; j++)
            {
                querys[queryIndex++] = keys[keyIndex];
            }
            keyIndex++;
        }
        Shuffle(querys);

        Stopwatch sw = new Stopwatch();
        // 测试 MoveToFrontArrayST
        sw.Start();
        for (int j = 0; j < querys.Length; j++)
        {
            mst.Get(querys[j]);
        }
        sw.Stop();
        Console.WriteLine("MoveToFrontArrayST: " + sw.ElapsedMilliseconds);

        // 测试 BinarySearchST
        sw.Restart();
        for (int j = 0; j < querys.Length; j++)
        {
            bst.Get(querys[j]);
        }
        sw.Stop();
        Console.WriteLine("BinarySearchST: " + sw.ElapsedMilliseconds);

        n *= 10;
    }
}

static void Shuffle<T>(T[] data)
{
    for (int i = 0; i < data.Length; i++)
    {
        int r = i + random.Next(data.Length - i);
        T temp = data[r];
        data[r] = data[i];
        data[i] = temp;
    }
}

另请参阅

SymbolTable 库

3.1.34

解答

在上一题的基础上进行修改即可，链接：{% post_link 3.1.33 %}。

调和级数 $ H_n = 1+frac{1}{2}+frac{1}{3} + cdots+frac{1}{n} $ 。
查询数组变为前 1/2 为 key[0]，随后的 1/3 为 key[1]，以此类推。
和上一题中的序列进行比较即可，注意删除最后的打乱步骤。

实验结果如下：

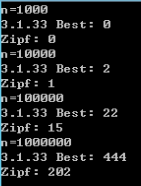
代码

首先建立一个数组计算调和级数，就像这样：

// 调和级数
double[] harmonicNumber = new double[1000 * (int)Math.Pow(10, 4)];
harmonicNumber[0] = 1;
for (int i = 1; i < harmonicNumber.Length; i++)
{
    harmonicNumber[i] = harmonicNumber[i - 1] + 1 / (i + 1);
}

然后修改构造查询的代码：

// 构造查询
Array.Sort(keys);
string[] queryZipf = new string[10 * n];
int queryIndex = 0, keyIndex = 0;
while (queryIndex < queryZipf.Length)
{
    int searchTimes = (int)Math.Ceiling(queryZipf.Length / (harmonicNumber[keyIndex + 1] * (i + 1)));

    for (int j = 0; j < searchTimes && queryIndex < queryZipf.Length; j++)
    {
        queryZipf[queryIndex++] = keys[keyIndex];
    }
    keyIndex++;
}

另请参阅

SymbolTable 库

3.1.35

解答

实验结果：

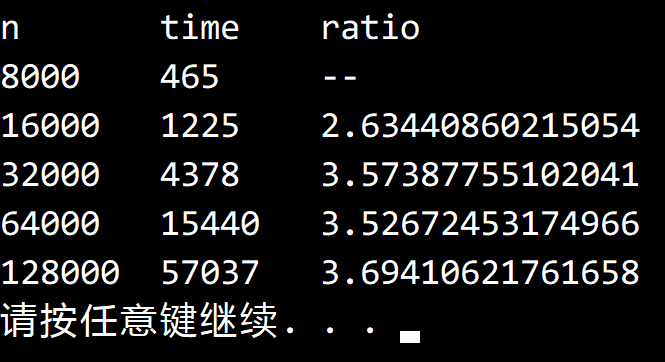
由于包含重复单词，因此结果会比 4 略低一些。
需要对 FrequencyCounter 做一些修改，令其只取前 n 个单词。

代码

static void Main(string[] args)
{
    int n = 8000;
    int multiplyBy2 = 5;
    int repeatTimes = 5;
    double lastTime = -1;
    Console.WriteLine("n	time	ratio");
    for (int i = 0; i < multiplyBy2; i++)
    {
        Console.Write(n + "	");
        long timeSum = 0;
        for (int j = 0; j < repeatTimes; j++)
        {
            SequentialSearchST<string, int> st = new SequentialSearchST<string, int>();
            Stopwatch sw = Stopwatch.StartNew();
            FrequencyCounter.MostFrequentlyWord("tale.txt", n, 0, st);
            sw.Stop();
            timeSum += sw.ElapsedMilliseconds;
        }
        timeSum /= repeatTimes;
        Console.Write(timeSum + "	");
        if (lastTime < 0)
            Console.WriteLine("--");
        else
            Console.WriteLine(timeSum / lastTime);
        lastTime = timeSum;
        n *= 2;
    }
}

另请参阅

SymbolTable 库

3.1.36

解答

实验结果如下，增长级为 O(N) ，但速度很快。

其实只要列出《双城记》不同长度的单词数目，原因就一目了然了。

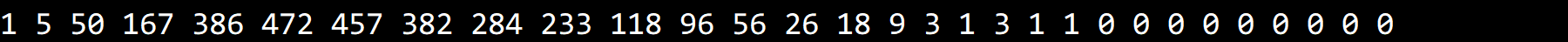
大部分单词都集中在中间长度，因此大部分访问也集中在数组中部。
二分查找在访问数组中部的元素时速度很快，因此结果好于预期。

代码

static void Main(string[] args)
{
    int n = 8000;
    int multiplyBy2 = 5;
    int repeatTimes = 5;
    double lastTime = -1;
    Console.WriteLine("n	time	ratio");
    for (int i = 0; i < multiplyBy2; i++)
    {
        Console.Write(n + "	");
        long timeSum = 0;
        for (int j = 0; j < repeatTimes; j++)
        {
            BinarySearchST<string, int> st = new BinarySearchST<string, int>();
            Stopwatch sw = Stopwatch.StartNew();
            FrequencyCounter.MostFrequentlyWord("tale.txt", n, 0, st);
            sw.Stop();
            timeSum += sw.ElapsedMilliseconds;
        }
        timeSum /= repeatTimes;
        Console.Write(timeSum + "	");
        if (lastTime < 0)
            Console.WriteLine("--");
        else
            Console.WriteLine(timeSum / lastTime);
        lastTime = timeSum;
        n *= 2;
    }
}

另请参阅

SymbolTable 库

3.1.37

解答

实验结果如下：

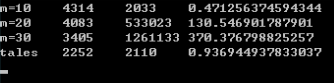
M=10 的时候随机的数字集中在 1024 到 2048 之间，重复值较多，因此 Put 耗时较少。
随着重复值的减少 Put 的耗时会大幅度提高，和实验结果显示的一样。
M=20 的时候数字在 1048576~2097152 之间随机，基本上没有重复值了。
M=30 的时候和 M=20 的情况类似，都是重复值几乎没有的情况。

随机数可以通过如下的方式产生：

result[i] = min + (long)(random.NextDouble() * (max - min));

代码

这里构造了 BinarySearchSTAnalysis 类，在类中声明了两个 Stopwatch 对象，
一个在 Put 方法的开始和结束部分进行计时，
另一个在 Get 方法的开始和结束部分进行计时。

static void Main(string[] args)
{
    int n = 1000000;
    int m = 10;
    int addBy10 = 3;

    for (int i = 0; i < addBy10; i++)
    {
        BinarySearchSTAnalysis<long, int> bst = new BinarySearchSTAnalysis<long, int>(n);
        long[] data = SearchCompare.GetRandomArrayLong(n, (long)Math.Pow(2, m), (long)Math.Pow(2, m + 1));
        FrequencyCounter.MostFrequentlyKey(bst, data);
        Console.WriteLine("m=" + m + "	" + bst.GetTimer.ElapsedMilliseconds + "	" + bst.PutTimer.ElapsedMilliseconds + "	" + bst.PutTimer.ElapsedMilliseconds / (double)bst.GetTimer.ElapsedMilliseconds);
        m += 10;
    }

    BinarySearchSTAnalysis<string, int> st = new BinarySearchSTAnalysis<string, int>();
    FrequencyCounter.MostFrequentlyWord("tale.txt", 0, st);
    Console.WriteLine("tales	" + st.GetTimer.ElapsedMilliseconds + "	" + st.PutTimer.ElapsedMilliseconds + "	" + st.PutTimer.ElapsedMilliseconds / (double)st.GetTimer.ElapsedMilliseconds);
    Console.ReadLine();
}

另请参阅

SymbolTable 库

3.1.38

解答

实验结果如下：
BinarySearchST

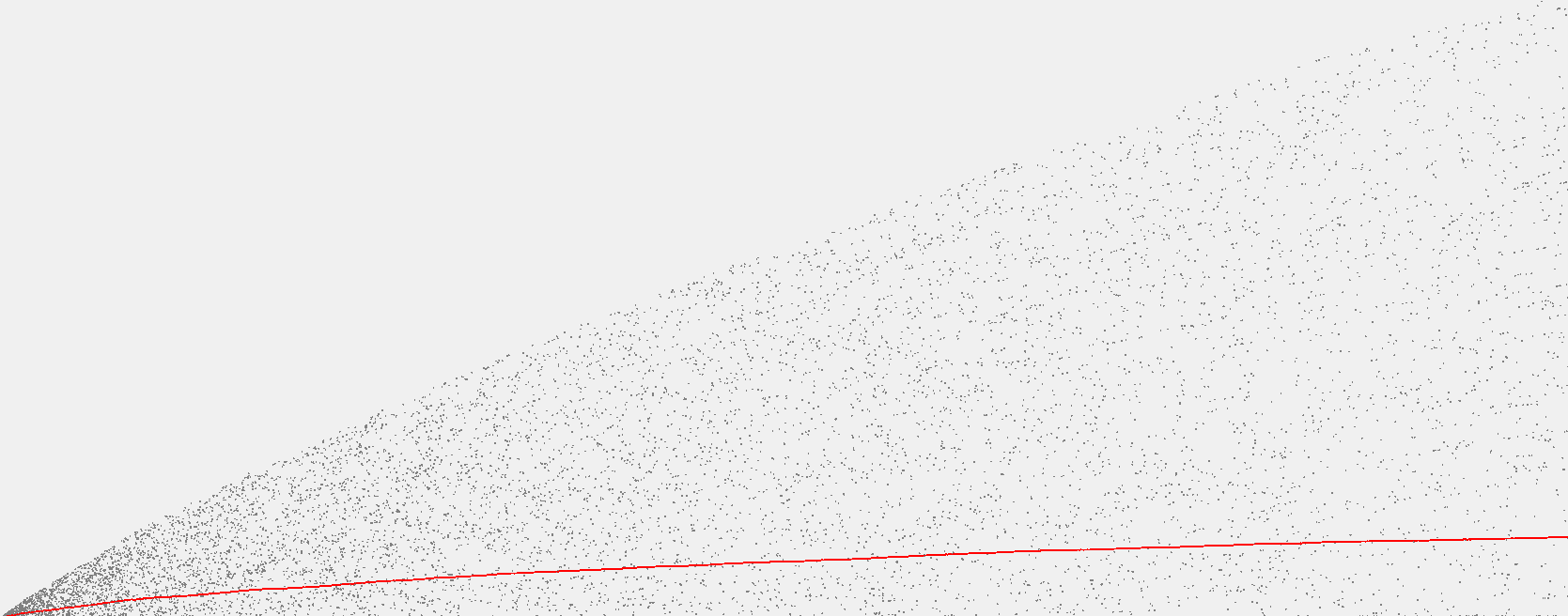
SequentialSearchST

对于 BinarySearchST ，每次比较之后以及移动元素时令 Cost 增加。
对于 SequentialSearchST，统计每次的查找次数即可。
然后绘制成散点图即可。

代码

有关绘图的函数，传入的参数为第 i 次 Put() 的开销。

public void Draw(int[] data)
{
    Graphics panel = this.CreateGraphics();
    float unitX = (float)this.ClientRectangle.Width / data.Length;
    float unitY = (float)this.ClientRectangle.Height / data.Max();

    int accumulation = 0;
    for (int i = 0; i < data.Length; i++)
    {
        // Gray
        panel.FillEllipse(Brushes.Gray, (i + 1) * unitX, this.ClientRectangle.Bottom - data[i] * unitY, 2, 2);
        // Red
        panel.FillEllipse(Brushes.Red, (i + 1) * unitX, this.ClientRectangle.Bottom - accumulation / (i + 1) * unitY, 2, 2);
        accumulation += data[i];
    }
}

另请参阅

SymbolTable 库

3.1.39

解答

实验结果如下：
BinarySearchST

SequentialSearchST

图像分为两段，分别代表不断向符号表中加入单词和寻找频率最大的单词两个部分。
第一段两个图像的形状类似（注意它们的 y 轴比例不同）。
第二段中 BinarySearchST 的表现要比 SequentialSearchST 稳定的多。

代码

绘图部分代码：

public void Draw(int[] x, long[] y)
{
    Graphics panel = this.CreateGraphics();

    float unitX = (float)this.ClientRectangle.Width / x.Max();
    float unitY = (float)this.ClientRectangle.Height / y.Max();

    for (int i = 0; i < x.Length; i++)
    {
        panel.FillEllipse(
            Brushes.Black,
            x[i] * unitX,
            this.ClientRectangle.Height - y[i] * unitY,
            2, 2);
    }
}

另请参阅

SymbolTable 库

3.1.40

解答

顺序查找平均需要进行 $ N/2 $ 次比较，二分查找则是 $ lg N $ 次。
列出方程可以解出 N 的大小

[egin {eqnarray*} 1000 log_2 N &=& N / 2 \ log_2 N &=& N / 2000\ frac{ln N}{ln 2} &=& N/2000 \ N &=& e^{frac{ln 2}{2000}N}\ 1 &=& Ne^{-frac{ln 2}{2000}N}\ N_1 = e^{-W(-frac{ln 2}{2000})}=1 & & N_2= e^{-W_{-1}(-frac{ln 2}{2000})}=29718\ \ end {eqnarray*} ]

这个方程是一个超越方程，最后的结果中出现了朗伯 W 函数。
同理可以求得 10000 倍的 N=369939。

实验结果如下：

由于存在缓存优化，每次比较的耗时并不相同。
因此实际耗时并未达到预期，但比较次数是符合预期的。

另请参阅

朗伯 W 函数-维基百科

3.1.41

解答

英文版描述为 1, 2, and 10 times faster。
即一样快，快一倍和快十倍（一个例子）。

和上题类似，也是解超越方程。
插值查找的平均查找次数为 $ lg(lg(N)) $。
可以解得 N = 1, 4, 58。

实验结果如下：

由于 N 太小，可以看到插值查找的运行时间几乎没有变化。