算法（第四版）C# 习题题解——1.1

写在前面

整个项目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp

善用 Ctrl + F 查找题目。

本节你可能会需要的两个测试数据文件：

largeW: http://algs4.cs.princeton.edu/11model/largeW.txt

largeT: http://algs4.cs.princeton.edu/11model/largeT.txt

习题 & 题解

练习（1.1.1~1.1.25）

1.1.1

解答

a.7
b.1562500.0015625
c.True

代码

        static void Main(string[] args)
        {
            int a = (0 + 15) / 2;
            double b = Math.Pow(2.0, -6) * 100000000.1; //Math.Pow(double x, double y) 求x的y次方
            bool c = true && false || true && true;

            //Console.WriteLine 向控制台窗口输出一行
            Console.WriteLine($"a.{a}");
            Console.WriteLine($"b.{b}");
            Console.WriteLine($"c.{c}");
        }

1.1.2

解答

        Name    Type            Value
        a       System.Double   1.618
        b       System.Double   10
        c       System.Boolean  True
        d       System.String   33

代码

        static void Main(string[] args)
        {
            //var 变量名 = 初始值  根据初始值自动判断变量类型
            var a = (1 + 2.236) / 2;
            var b = 1 + 2 + 3 + 4.0;
            var c = 4.1 >= 4;
            var d = 1 + 2 + "3";

            //Console.WriteLine 向控制台输出一行
            //变量名.GetType() 返回变量类型
            //Type.ToString() 将类型名转换为字符串

            Console.WriteLine("	Name	Type     	Value");
            Console.WriteLine($"	a	{a.GetType().ToString()}	{a}");
            Console.WriteLine($"	b	{b.GetType().ToString()}	{b}");
            Console.WriteLine($"	c	{c.GetType().ToString()}	{c}");
            Console.WriteLine($"	d	{d.GetType().ToString()}	{d}");
        }

1.1.3

解答

简单的 if 判断即可

代码

        static void Main(string[] args)
        {
            //Console.ReadLine() 从控制台读入一整行（返回int）
            //string.Split(char) 根据提供的分隔符将字符串分割，返回字符串数组
            //Int32.Parse(string) 将字符串转换为相应的整型数据
            string input = Console.ReadLine();
            int a = Int32.Parse(input.Split(' ')[0]);
            int b = Int32.Parse(input.Split(' ')[1]);
            int c = Int32.Parse(input.Split(' ')[2]);

            //Console.WriteLine() 向控制台输出一行
            if (a == b && b == c)
            {
                Console.WriteLine("equal");
            }
            else
            {
                Console.WriteLine("not equal");
            }
        }

1.1.4

解答

a. if 后跟 then 的语法不能在 C# 中使用。

b. if 后的判断语句需要在括号内。

c. 正确，只有一条语句时大括号可以省略。

d. c = 0 后缺少分号。

代码

static void Main(string[] args)
        {
            int a = 1;
            int b = 2;
            int c = 0;

            //if (a > b) then c = 0; 
            //if 后不能跟 then

            //if a > b { c = 0; } 
            //if后必须跟括号

            if (a > b) c = 0;
            //正确

            //if (a > b) c = 0 else b = 0; 
            //c = 0后缺少分号

        }

1.1.5

解答

比较简单，直接判断即可。

代码

static void Main(string[] args)
        {
            //修改这两个值进行测试
            double x = 0.05;
            double y = 0.01;

            if (x > 0 && x < 1 && y > 0 && y < 1)
            {
                Console.WriteLine("true");
            }
            else
            {
                Console.WriteLine("false");
            }
        }

1.1.6

解答

输出斐波那契数列。

将书中的代码直接实现即可。

代码

//输出斐波那契数列
        static void Main(string[] args)
        {
            int f = 0;
            int g = 1;
            for (int i = 0; i <= 15; i++)
            {
                //Console.WriteLine与StdOut.println功能相同
                //实现向控制台输出一行
                Console.WriteLine(f);
                f = f + g;
                g = f - g;
            }
        }

1.1.7

解答

同上题，直接实现即可。

a
3.00009

double计算存在误差，并不精确。

b
499500

1000 + 999 + 998……

c
10000

1000 * 10，外层循环的结束条件为 2ⁱ > 1000。

代码

private static void a()
        {
            Console.WriteLine("a");
            double t = 9.0;
            while (Math.Abs(t - 9.0 / t) > .001)
            {
                t = (9.0 / t + t) / 2.0;
            }
            Console.Write($"{t:N5}
");//:N5代表保留5位小数，同理可使用N1、N2……
        }

        private static void b()
        {
            Console.WriteLine("
b");
            int sum = 0;
            for (int i = 1; i < 1000; i++)
            {
                for (int j = 0; j < i; j++)
                {
                    sum++;
                }
            }
            Console.WriteLine(sum);
        }

        private static void c()
        {
            Console.WriteLine("
c");
            int sum = 0;
            for (int i = 1; i < 1000; i *= 2)
            {
                for (int j = 0; j < 1000; j++)
                {
                    sum++;
                }
            }
            Console.WriteLine(sum);
        }

        static void Main(string[] args)
        {
            //a double 计算存在误差
            a();

            //b 1000+999+998……
            b();

            //c 由于2^10 = 1024 > 1000，最终sum = 1000 * 10 = 10000
            c();
        }

1.1.8

解答

b
197
e

代码

static void Main(string[] args)
        {
            Console.WriteLine('b');
            Console.WriteLine('b' + 'c'); //char 被隐式转为为 int 类型，取 ascii 码
            Console.WriteLine((char)('a' + 4)); //强制转换后，ascii 码被转换为相应的字符
        }

1.1.9

解答

有两种方法，要么直接调用库函数，要么用书中给出的代码转换。

代码

static void Main(string[] args)
        {
            int N = 4;

            //1.直接转换 Convert.ToString(int, int) 第一个为要转换的数，第二个为要转换的进制
            Console.WriteLine($"{Convert.ToString(N, 2)}");

            //2.转换为二进制数
            string s = "";
            for (int n = N; n > 0; n /= 2)
            {
                s = (n % 2) + s;
            }
            Console.WriteLine(s);
        }

1.1.10

解答

变量使用前需要先赋值。

代码

static void Main(string[] args)
        {
            int[] a;
            for (int i = 0; i < 10; i++)
            {
                a[i] = i * i; //不允许使用未赋值的局部变量
            }
        }

1.1.11

解答

注意，二维数组 bool[M, N] 代表 M 行 N 列的布尔数组。

使用二重循环即可实现。

输出使用制表符 ’ ’ 作为分隔。

代码

static void PrintArray2D(bool[,] array)
        {
            int rows = array.GetLength(0);//获取行数
            int columns = array.GetLength(1);//获取列数

            //输出列号
            for (int i = 0; i < columns; i++)
            {
                Console.Write($"	{i + 1}");
            }

            Console.Write("
");

            for (int i = 0; i < rows; i++)
            {
                //输出行号
                Console.Write($"{i + 1}");
                for (int j = 0; j < columns; j++)
                {
                    if (array[i, j])
                    {
                        Console.Write($"	*");
                    }
                    else
                    {
                        Console.Write($"	 ");
                    }
                }
                Console.Write("
");
            }
        }

1.1.12

解答

第一个循环初始化数组{9, 8, 7, 6, 5, 4, 3, 2, 1, 0}

第二个循环用相应位置的值作为下标取值，例如：a[0] = a[a[0]] = a[9] = 0

最后结果为：0,1,2,3,4,4,3,2,1,0

代码

static void Main(string[] args)
        {
            int[] a = new int[10];
            for (int i = 0; i < 10; i++)
            {
                a[i] = 9 - i;
            }
            //a[10] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0}
            for (int i = 0; i < 10; i++)
            {
                a[i] = a[a[i]];
            }
            //a[0] = a[9] = 0; a[1] = a[8] = 1; a[2] = a[7] = 2;......
            for (int i = 0; i < 10; i++)
            {
                Console.WriteLine(a[i]);
            }
        }

1.1.13

解答

转置输出只需要在二重循环的时候将行、列输出顺序取反即可。

代码

static void Main(string[] args)
        {
            int M = 2;
            int N = 3;
            int[,] array = new int[M, N];

            //新建一个二维数组
            for (int i = 0; i < M; i++)
            {
                for (int j = 0; j < N; j++)
                {
                    array[i, j] = i + j;
                }
            }

            Console.WriteLine("Origin");
            PrintArray2D(array, M, N);

            Console.WriteLine("Transposed");
            PrintArrayTranspose2D(array, M, N);
        }

        //转置输出
        private static void PrintArrayTranspose2D(int[,] array, int rows, int columns)
        {
            //交换行、列输出顺序
            for (int i = 0; i < columns; i++)
            {
                for (int j = 0; j < rows; j++)
                {
                    Console.Write($"	{array[j, i]}");
                }
                Console.Write("
");
            }
        }

        //正常输出
        private static void PrintArray2D(int[,] array, int rows, int columns)
        {
            for (int i = 0; i < rows; i++)
            {
                for (int j = 0; j < columns; j++)
                {
                    Console.Write($"	{array[i, j]}");
                }
                Console.Write("
");
            }
        }

1.1.14

解答

简单使用 log 的定义逼近即可。

代码

static void Main(string[] args)
        {
            int N = 9;
            Console.WriteLine($"{ lg(N)}");
        }

        //利用循环逼近 N，得到 log2(N) 的值
        static int lg(int N)
        {
            int baseNumber = 2;
            int pow = 1;
            int sum = 2;

            for (pow = 1; sum < N; ++pow)
            {
                sum *= baseNumber;
            }

            return pow - 1;
        }

1.1.15

解答

利用二重循环，查找每个值在数组中出现的次数。

代码

static void Main(string[] args)
        {
            int[] a = new int[10];
            int M = 10;
            for (int i = 0; i < 10; ++i)
            {
                a[i] = i;
            }

            int[] result = Histogram(a, M);

            Console.WriteLine($"a.length: {a.Length}");
            Console.WriteLine($"sum of result array: {result.Sum()}");
        }

        static int[] Histogram(int[] a, int M)
        {
            int[] result = new int[M];

            for (int i = 0; i < M; ++i)
            {
                //初始化
                result[i] = 0;

                //遍历数组，计算数组中值为 i 的元素个数
                for (int j = 0; j < a.Length; ++j)
                {
                    if (a[j] == i) //值为 i 的元素
                    {
                        result[i]++;
                    }
                }
            }

            return result;
        }

1.1.16

解答

填入代码测试即可。

用字符串拼接的方式展示递归。

类似于这个：

代码

static void Main(string[] args)
        {
            Console.WriteLine($"{exR1(6)}");
        }

        //exR1(6) = 
        //exR1(3) + 6 + exR1(4) + 6
        //exR1(0) + 3 + exR1(1) + 3 + 6 + exR1(4) + 6
        //"" + 3 + exR1(-2) + 1 + exR1(-1) + 1 + 3 + 6 + exR1(4) + 6
        //"" + 3 + "" + 1 + "" + 1 + 3 + 6 + exR1(4) + 6
        //"31136" + exR1(4) + 6
        //......

        public static string exR1(int n)
        {
            if (n <= 0)
            {
                return "";
            }

            return exR1(n - 3) + n + exR1(n - 2) + n;
        }

1.1.17

解答

书中已经给出了解释。

递归时结束条件必须放在递归语句的前面，否则会不断展开而无法结束。

代码

static void Main(string[] args)
        {
            Console.WriteLine($"{exR2(6)}");//抛出 StackOverflow Exception
        }

        public static string exR2(int n)
        {
            string s = exR2(n - 3) + n + exR2(n - 2) + n;//运行到 exR2 即展开，不会再运行下一句
            if (n <= 0) return "";
            return s;
        }

1.1.18

解答

其实就是一种快速乘法的实现，换成乘号之后就变成了快速乘幂。

例如对于乘法 2 * 4，可以用 2 + 2 + 2 + 2 做四次加法计算；也可以变为 (2 + 2) * 2 = (2 + 2) + (2 + 2) 的形式，用两次加法就可以完成（先计算 2 + 2 的值，再计算 4 + 4 的值）。

同理对于乘幂 2⁸，既可以用 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 做 8 次乘法，也可以只用三次乘法就计算出来：

2² = 2 * 2

2⁴ = 2² * 2²

2⁸ = 2⁴ * 2⁴

这样时间复杂度就从 O(n) 变为了 O(log n)。

代码

static void Main(string[] args)
        {
            Console.WriteLine($"mystery(2, 25): {mystery(2, 25)}");
            Console.WriteLine($"mystery(3, 11): {mystery(3, 11)}");

            Console.WriteLine($"mysteryChanged(2, 8): {mysteryChanged(2, 8)}");
            Console.WriteLine($"mysteryChanged(3, 2): {mysteryChanged(3, 2)}");
        }

        //mystery(a, b) = a * b
        //利用等式：a * b = 2a * b/2 = (2a * (b-1) / 2) + a
        //示例：
        //mystery(2, 25) =
        //mystery(2 + 2, 12) + 2 =
        //mystery(4 + 4, 6) + 2 =
        //mystery(8 + 8, 3) =
        //mystery(16 + 16, 1) + 16 + 2 =
        //mystery(32 + 32, 0) + 32 + 16 + 2 =
        //0 + 32 + 16 + 2 =
        //50
        public static int mystery(int a, int b)
        {
            if (b == 0) return 0;
            if (b % 2 == 0) return mystery(a + a, b / 2);
            return mystery(a + a, b / 2) + a;
        }

        //mysteryChanged(a, b) = a ^ b
        //同理（乘方与乘法，乘法与加法之间具有类似的性质）
        //a ^ b = (a ^ 2) ^ (b / 2) = (a ^ 2) ^ ((b - 1) / 2) * a
        public static int mysteryChanged(int a, int b)
        {
            if (b == 0) return 1;
            if (b % 2 == 0) return mysteryChanged(a * a, b / 2);
            return mysteryChanged(a * a, b / 2) * a;
        }

1.1.19

解答

普通的递归算法效率很低，原因是越到后面重复运算的数目越多。

比如：

F(2) = F(1) + F(0)

F(3) = F(2) + F(1) = F(1) + F(1) + F(0)

可以看到 F(1) 被重复计算了两次。

改进的方式是将每次运算的结果保存在数组中，之后计算过的数据直接从数组中提取。

代码

class Fibnacci
    {
        //long 类型不够大，换成 UINT64 类型
        //用于保存计算结果的数组，UInt64? 代表可以赋值为普通 UInt64 类型的值以及 null 值
        private static UInt64?[] fibnacciResults = new UInt64?[100];
        
        static void Main(string[] args)
        {
            /*
             * 测试环境
             * 
             * Surface Pro3 i7
             * i7 4650U + 8G
             * 
             */
            Stopwatch timer = Stopwatch.StartNew();
            for (int N = 0; N < 100; ++N)
            {
                //书本中的代码，非常慢，1小时后 N = 50
                //Console.WriteLine($"{N} {F(N)}");

                //利用已知结果加速
                //全部计算完毕耗时 84ms
                Console.WriteLine($"{N} {BetterF(N)}");
            }
            Console.WriteLine($"{timer.ElapsedMilliseconds} ms");
        }

        //书中提供的代码
        public static UInt64 F(int N)
        {
            if (N == 0)
                return 0;
            if (N == 1)
                return 1;

            return F(N - 1) + F(N - 2);
        }

        //更好的实现，将已经计算的结果保存，不必重复计算
        public static UInt64? BetterF(int N)
        {
            if (N == 0)
                return 0;
            if (N == 1)
                return 1;

            if (fibnacciResults[N] != null)     //如果已经计算过则直接读取已知值
            {
                return fibnacciResults[N];
            }
            else
            {
                fibnacciResults[N] = BetterF(N - 1) + BetterF(N - 2);
                return fibnacciResults[N];
            }
        }
    }

1.1.20

解答

根据对数的性质可以得到：

ln(N!) = ln(N) + ln(N – 1) + ln(N – 2)…

代码

static void Main(string[] args)
        {
            int N = 4;
            Console.WriteLine($"{factorialLn(N)}");
        }

        //ln(N!) =
        //ln(N * (N - 1) * ... * 1) =
        //ln(N) + ln((N - 1)!)
        public static double factorialLn(int N)
        {
            if (N == 1)
            {
                return 0;
            }

            return Math.Log(N) + factorialLn(N - 1);
        }

1.1.21

解答

实现上没什么难度，打印表格的部分可以参考之前打印二位布尔数组的方法。

注意整型数据之间相除得到的仍然是整型，小数部分会直接舍去，例如 2 / 3 = 0。

代码

static void Main(string[] args)
        {
            int columns = 2;
            int rows = int.Parse(Console.ReadLine());   //行号

            string[] names = new string[rows];          //姓名
            int[,] array = new int[rows, columns];      //输入的两个整数
            double[] results = new double[rows];        //计算结果

            for (int i = 0; i < rows; ++i)
            {
                string temp = Console.ReadLine();
                names[i] = temp.Split(' ')[0];
                for (int j = 0; j < columns; ++j)
                {
                    array[i, j] = int.Parse(temp.Split(' ')[j + 1]);
                }
                results[i] = (double)array[i, 0] / array[i, 1];
            }

            PrintArray2D(names, array, results);
        }

        static void PrintArray2D(string[] names, int[,] array, double[] results)
        {
            int rows = array.GetLength(0);//获取行数
            int columns = array.GetLength(1);//获取列数

            for (int i = 0; i < rows; i++)
            {
                Console.Write($"	{names[i]}");
                for (int j = 0; j < columns - 1; j++)
                {
                    Console.Write($"	{array[i, j]}");
                }
                Console.Write($"	{array[i, columns - 1]}");
                Console.Write($"	{results[i]:N3}");    //变量名:N3 保留三位小数
                Console.Write("
");
            }
        }

1.1.22

解答

按照书中的提示增加一个保存深度的参数。

代码

class BinarySearch
    {
        static void Main(string[] args)
        {
            int[] array = new int[10] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };

            rank(9, array);
        }

        //重载方法，用于启动二分查找
        public static int rank(int key, int[] a)
        {
            return rank(key, a, 0, a.Length - 1, 1);
        }

        //二分查找
        public  static int rank(int key, int[] a, int lo, int hi, int number)
        {

            for (int i = 0; i < number; ++i)
            {
                Console.Write(" ");
            }
            Console.WriteLine($"{number}: {lo} {hi}");

            if (lo > hi)
            {
                return -1;
            }

            int mid = lo + (hi - lo) / 2;

            if (key < a[mid])
            {
                return rank(key, a, lo, mid - 1, number + 1);
            }
            else if (key > a[mid])
            {
                return rank(key, a, mid + 1, hi, number + 1);
            }
            else
            {
                return mid;
            }
        }
    }

1.1.23

解答

在主函数里做一下判断就可以了，加号则输出所有找不到的值，减号则相反。

代码

static void Main(string[] args)
        {
            //从largeW.txt中读取数据
            string[] whiteList = File.ReadAllLines("largeW.txt");
            int[] WhiteList = new int[whiteList.Length];
            
            for (int i = 0; i < whiteList.Length; ++i)
            {
                WhiteList[i] = int.Parse(whiteList[i]);
            }

            Array.Sort<int>(WhiteList);

            Console.WriteLine("Type the numbers you want to query: ");
            //输入样例：5 824524 478510 387221
            string input = Console.ReadLine();
            int[] Query = new int[input.Split(' ').Length];
            for (int i = 0; i < Query.Length; ++i)
            {
                Query[i] = int.Parse(input.Split(' ')[i]);
            }

            Console.WriteLine("Type '+' to get the numbers that not in the whitelist," + 
                "'-' to get the numbers that in the whitelist.");
            char operation = Console.ReadLine()[0];

            foreach (int n in Query)
            {
                if (rank(n, WhiteList) == -1)
                {
                    if (operation == '+')
                    {
                        Console.WriteLine(n);
                    }
                }
                else if (operation == '-')
                {
                    Console.WriteLine(n);
                }
            }
        }

        //重载方法，用于启动二分查找
        public static int rank(int key, int[] a)
        {
            return rank(key, a, 0, a.Length - 1);
        }

        //二分查找
        public static int rank(int key, int[] a, int lo, int hi)
        {

            if (lo > hi)
            {
                return -1;
            }

            int mid = lo + (hi - lo) / 2;

            if (key < a[mid])
            {
                return rank(key, a, lo, mid - 1);
            }
            else if (key > a[mid])
            {
                return rank(key, a, mid + 1, hi);
            }
            else
            {
                return mid;
            }
        }

1.1.24

解答

在书本中 GCD 的基础上，在函数开始时增加一条输出语句即可。

代码

static void Main(string[] args)
        {
            GCD(105, 24);
            Console.WriteLine();
            GCD(111111, 1234567);
        }

        public static int GCD(int a, int b)
        {
            Console.WriteLine($"{a} {b}");
            if (b == 0)
            {
                return a;
            }

            return GCD(b, a % b);
        }

1.1.25

解答

证明见代码。

也可以访问维基百科：辗转相除法

代码

namespace _1._1._25
{
    /*
     * 1.1.25
     * 
     * 用数学归纳法证明欧几里得算法能够计算出任意一对非负整数 p 和 q 的最大公约数
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            /* 证明：
             * 
             * 已知： a, b 皆为正整数，且 a > b。g 是 a、b 的最大公约数
             * 设 r0 = a % b, rk = rk-2 % rk-1
             * 那么有 gcd(a, b) = gcd(b, r0) = gcd(r0, r1)... = gcd(rn-1, rn)
             * 且 rn = 0 （此时算法终止）
             * 
             * 由于 rn-2 = qn * rn - 1 + rn = qn * rn-1 （qn = [rn-2 / rn-1] []代表向下取整)
             * 可得 rn-2 能被 rn-1 整除
             * 则 
             * rn-3 = qn-1 * rn-2 + rn-1 
             * = qn-1 * (qn * rn-1) + rn-1 （代入 rn-2 = qn * rn-1）
             * = qn-1 * qn * rn-1 + rn-1
             * = (qn-1 * qn + 1) * rn-1
             * 可得 rn-3 也能被 rn-1 整除
             * 以此类推，rn-1 可以整除 a 和 b，即 rn-1 是 a 和 b 的公约数
             * 则 rn-1 <= g
             * 
             * 因为 g 是 a、b 的最大公约数，由性质可得：
             * a = mg, b = ng （m、n 是自然数）
             * 
             * r0 
             * = a % b 
             * = a - q0 * b （q0 = [a / b] []代表向下取整）
             * = mg - q0 * ng （代入 34 行的结论）
             * = (m - q0 * n)g
             * 
             * 可得 r0 能被 g 整除
             * 同理 r1, r2, r3, ..., rn-1 都可以被 g 整除
             * 因此 g <= rn-1
             * 
             * 综合 31 行和 44 行的结论可得 rn-1 = g
             * 
             * 证明完毕
             */
        }

        static int gcd(int p, int q)
        {
            if (q == 0)
            {
                return p;
            }

            int r = p % q;

            return gcd(q, r);
        }
    }
}

提高题（1.1.26~1.1.34）

1.1.26

解答

见代码部分。

代码

static void Main(string[] args)
        {
            int a = 3;
            int b = 2;
            int c = 1;
            int t = 0;

            if (a > b) { t = a; a = b; b = t; } //如果 a > b，那么 a, b 交换，保证b >= a
            if (a > c) { t = a; a = c; c = t; } //如果 b >= a > c，那么 a, c 交换，保证 c >= a
            if (b > c) { t = b; b = c; c = t; } //如果 b > c >= a，那么 b, c 交换，保证 c >= b
            Console.WriteLine($"{a} {b} {c}");  //最终结果为 c >= b >= a，保证升序排列
        }

1.1.27

解答

与之前的斐波那契数列类似，都是重复计算的问题。

7751次。

代码

class Program
    {
        static int BinomialCalled = 0;  //计算递归调用次数
        static double?[,] BinomialCache;    //保存计算结果的数组

        static void Main(string[] args)
        {
            BinomialCache = new double?[101, 51];
            Console.WriteLine(Binomial(100, 50, 0.25));
            Console.WriteLine(BinomialCalled);
        }

        public static double? Binomial(int N, int k, double p)
        {
            BinomialCalled++;
            if (N == 0 && k == 0)
                return 1.0;
            if (N < 0 || k < 0)
                return 0.0;
            if (BinomialCache[N, k] != null)
            {
                return BinomialCache[N, k];
            }
            else
            {
                BinomialCache[N, k] = (1.0 - p) * Binomial(N - 1, k, p) + p * Binomial(N - 1, k - 1, p);
                return BinomialCache[N, k];
            }
        }
    }

1.1.28

解答

实现方法有很多，这里是使用一个 HashSet 做中转，删除所有的重复元素。

也可以使用 Linq 里的 Distinct() 方法，

也可以排序后直接遍历一遍，遇到相同的就删除，遇到不同的就保存起来用于之后的比较。

代码

static void Main(string[] args)
        {
            //从largeW.txt中读取数据
            //用 HashSet 的不可重复性去除重复
            HashSet<string> h = new HashSet<string>(File.ReadAllLines("largeW.txt"));
            string[] whiteList = new string[h.Count];
            h.CopyTo(whiteList);
            int[] WhiteList = new int[whiteList.Length];

            for (int i = 0; i < whiteList.Length; ++i)
            {
                WhiteList[i] = int.Parse(whiteList[i]);
            }

            Array.Sort<int>(WhiteList);

            Console.WriteLine("Type the numbers you want to query: ");
            //输入样例：5 824524 478510 387221
            string input = Console.ReadLine();
            int[] Query = new int[input.Split(' ').Length];
            for (int i = 0; i < Query.Length; ++i)
            {
                Query[i] = int.Parse(input.Split(' ')[i]);
            }

            Console.WriteLine("Irrelevant:");
            foreach (int n in Query)
            {
                if (rank(n, WhiteList) == -1)
                {
                    Console.WriteLine(n);
                }
            }
        }

        //重载方法，用于启动二分查找
        public static int rank(int key, int[] a)
        {
            return rank(key, a, 0, a.Length - 1);
        }

        //二分查找
        public static int rank(int key, int[] a, int lo, int hi)
        {

            if (lo > hi)
            {
                return -1;
            }

            int mid = lo + (hi - lo) / 2;

            if (key < a[mid])
            {
                return rank(key, a, lo, mid - 1);
            }
            else if (key > a[mid])
            {
                return rank(key, a, mid + 1, hi);
            }
            else
            {
                return mid;
            }
        }

1.1.29

解答

查找小于指定值的元素数量可以多次使用二分查找实现。

例如：

序号：0 1 2 3 4 5 6 7 8

元素：1 2 2 2 2 2 2 2 3

二分查找返回 4

再次在 0~3 之间查找

二分查找返回 1

再次在 0~1 之间查找

二分查找返回 -1，没有指定值了

因此小于该值的元素数量就是 1 – 0 = 1 个

用同样的方法可以找到大于指定值的元素个数，从总数中减去这两个数值就是等于指定值的元素数量。

代码

static void Main(string[] args)
        {
            int[] WhiteList = new int[] { 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6 };

            Array.Sort<int>(WhiteList);

            Console.WriteLine("Type the numbers you want to query: ");
            string input = Console.ReadLine();
            int[] Query = new int[input.Split(' ').Length];
            for (int i = 0; i < Query.Length; ++i)
            {
                Query[i] = int.Parse(input.Split(' ')[i]);
            }

            Console.WriteLine("Result:");
            foreach (int n in Query)
            {
                int less = rank(n, WhiteList);
                int equal = count(n, WhiteList);
                Console.WriteLine($"Less: {less} Equal: {equal}");
            }
        }

        //返回数组中相等元素的个数
        public static int count(int key, int[] a)
        {
            int lowerBound = rank(key, a);
            int upperBound = lowerBound;

            if (lowerBound == -1)
                return 0;

            int result = 0;
            while (true)
            {
                result = rank(key, a, upperBound + 1, a.Length - 1);
                if (result == -1)
                    break;
                if (result > upperBound)
                {
                    upperBound = result;
                }
            }

            return upperBound - lowerBound + 1;
        }

        //返回数组中小于该数的数字个数
        public static int rank(int key, int[] a)
        {
            int mid = rank(key, a, 0, a.Length - 1);
            if (mid == -1)
                return 0;
            int result = mid;
            while (true)
            {
                result = rank(key, a, 0, mid - 1);

                if (result == -1)
                    break;
                if (result < mid)
                    mid = result;
            }
            return mid;
        }

        //二分查找
        public static int rank(int key, int[] a, int lo, int hi)
        {

            if (lo > hi)
            {
                return -1;
            }

            int mid = lo + (hi - lo) / 2;

            if (key < a[mid])
            {
                return rank(key, a, lo, mid - 1);
            }
            else if (key > a[mid])
            {
                return rank(key, a, mid + 1, hi);
            }
            else
            {
                return mid;
            }
        }
    }

1.1.30

解答

互质可以用之前的 GCD 最大公因数算法判断，如果最大公因数是 1 则两数互质。

代码

//互质 = 最大公约数为 1 = gcd(i, j) == 1
        static void Main(string[] args)
        {
            int N = int.Parse(Console.ReadLine());

            bool[,] a = new bool[N, N];

            for (int i = 0; i < N; ++i)
            {
                for (int j  = 0; j < N; ++j)
                {
                    a[i, j] = (gcd(i, j) == 1);
                }
            }

            PrintArray2D(a, N, N);
        }

        static int gcd(int a, int b)
        {
            if (b == 0)
                return a;

            return gcd(b, a % b);
        }

        private static void PrintArray2D(bool[,] array, int rows, int columns)
        {
            for (int i = 0; i < rows; i++)
            {
                for (int j = 0; j < columns; j++)
                {
                    Console.Write($"	{array[i, j]}");
                }
                Console.Write("
");
            }
        }
    }

1.1.31

解答

概率的实现方法：

例如概率是 60 %，就在 [0, 100) 之间随机一个值，小于等于 60 则执行操作，反之不执行。

需要更精确的情况可以增大随机的范围，例如 [0, 1000)。

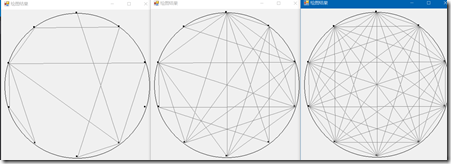
绘图结果：

N = 10,p = 0.2, 0.5, 1

完整项目可以到 Github 上下载。

代码（绘图部分）

/// <summary>
        /// 主绘图函数
        /// </summary>
        /// <param name="N">点的总数目</param>
        /// <param name="p">每对点之间连接的概率</param>
        public static void StartDrawing(int N, double p)
        {
            int pointSize = 5;//每个点绘制的大小
            int precious = 1000;//概率判断的精度

            //新建一个绘图窗口
            Form2 DrawPad = new Form2();
            //显示绘图窗口
            DrawPad.Show();

            //新建画布
            Graphics graphics = DrawPad.CreateGraphics();

            //建立绘图区域（矩形）
            Rectangle rect = new Rectangle(10, 10, 400, 400);
            
            //画圆
            graphics.DrawEllipse(Pens.Black, rect);

            //计算旋转角度
            double rotateDgree = 360.0 / N;

            //计算点的坐标
            Point Center = new Point(rect.Top + rect.Height / 2, rect.Top + rect.Height / 2);
            Point[] points = new Point[N];
            points[0].X = rect.Left + rect.Width / 2;
            points[0].Y = rect.Top;

            for (int i = 1; i < N; ++i)
            {
                points[i] = Rotate(Center, points[i - 1], rotateDgree);
            }

            //绘制点
            foreach (Point point in points)
            {
                graphics.FillEllipse(Brushes.Black, point.X - pointSize, point.Y - pointSize, pointSize, pointSize);
            }

            //按照概率绘制直线
            Random random = new Random();
            for (int i = 0; i < N; ++i)
            {
                for (int j = i + 1; j < N; ++j)
                {
                    //举例：输入概率为 0.6，精度为 1000
                    //在 0~1000 范围内等概率取值，如果小于等于 600 则视为事件发生
                    if (random.Next(0, precious) <= p * precious)
                    {
                        graphics.DrawLine(Pens.Gray, points[i], points[j]);
                    }
                }
            }

            //释放资源
            graphics.Dispose();
        }

        /// <summary>
        /// 计算一个点绕某点旋转之后的坐标值
        /// </summary>
        /// <param name="origin">旋转的圆心</param>
        /// <param name="point">需要旋转的点</param>
        /// <param name="dgree">旋转的角度（逆时针）</param>
        /// <returns>返回旋转后的坐标</returns>
        public static Point Rotate(Point origin, Point point, double dgree)
        {
            Point rotated = new Point();
            double dgreePi = dgree / 180 * Math.PI;

            rotated.X = (int)((point.X - origin.X) * Math.Cos(dgreePi) -
                (point.Y - origin.Y) * Math.Sin(dgreePi) + origin.X);
            rotated.Y = (int)((point.X - origin.X) * Math.Sin(dgreePi) +
                (point.Y - origin.Y) * Math.Cos(dgreePi) + origin.Y);

            return rotated;
        }

1.1.32

解答

绘图结果：

完整的项目代码可以去 Github 上下载。

代码（绘图部分）

public static void StartDrawing(double[] array, int N, double l, double r)
        {
            //创建并显示绘图窗口
            Form2 DrawPad = new Form2();
            DrawPad.Show();

            //新建画布
            Graphics graphics = DrawPad.CreateGraphics();
            
            //翻转默认坐标系
            graphics.TranslateTransform(0, DrawPad.Height);
            graphics.ScaleTransform(1, -1);

            //对原始数组排序
            Array.Sort(array);

            //计算各区域的值
            int[] counts = new int[N];
            int index = 0;
            for (int i = 0; i < N; ++i)
            {
                for (int j = index; j < array.Length; ++j)
                {
                    if (array[j] <= (r - l) * (i + 1) / N)
                    {
                        counts[i]++;
                        index++;
                    }
                    else
                    {
                        break;
                    }
                }
            }

            //获取最大值
            double max = counts.Max();
            //计算间距
            double unit = DrawPad.Width / (3.0 * N + 1);
            //计算直方图的矩形
            Rectangle[] rects = new Rectangle[N];
            rects[0].X = (int)unit;
            rects[0].Y = 0;
            rects[0].Width = (int)(2 * unit);
            rects[0].Height = (int)((counts[0] / max) * DrawPad.Height);
            for (int i = 1; i < N; ++i)
            {
                rects[i].X = (int)(rects[i - 1].X + 3 * unit);
                rects[i].Y = 0;
                rects[i].Width = (int)(2 * unit);
                rects[i].Height = (int)((counts[i] / (max + 1)) * DrawPad.Height);
            }

            //绘图
            graphics.FillRectangles(Brushes.Black, rects);

            //释放资源
            graphics.Dispose();
        }

1.1.33

解答

这里矩阵使用交错数组实现（方便取行向量），不是普通的二维数组。

矩阵和矩阵、矩阵和向量、向量和矩阵都使用行向量点乘列向量的方式计算。

代码

public class Matrix
    {
        /// <summary>
        /// 计算两个向量的点积
        /// </summary>
        /// <param name="x">需要点乘的向量</param>
        /// <param name="y">需要点乘的另一个向量</param>
        /// <returns>返回点乘的结果</returns>
        /// <exception cref="FormatException"></exception>
        public static double Dot(double[] x, double[] y)
        {
            //确保两向量等长
            if (x.Length != y.Length)
            {
                throw new FormatException("the length of two vectors must be equal");
            }

            //点乘
            double result = 0;
            for (int i = 0; i < x.Length; ++i)
            {
                result += x[i] * y[i];
            }

            return result;
        }

        /// <summary>
        /// 计算两个矩阵相乘的结果，返回一个矩阵
        /// </summary>
        /// <param name="a">用交错数组表示的 m * p 矩阵</param>
        /// <param name="b">用交错数组表示的 p * n 矩阵</param>
        /// <returns>返回 m * n 的矩阵</returns>
        /// <exception cref="FormatException"></exception>
        /// <example>
        ///     a = {(1,2,3),(4,5,6)}
        ///     b = {(1,4),(2,5),(3,6)}
        ///     Mult(a, b) = {(14,32),(32,77)}
        /// </example>
        public static double[][] Mult(double[][] a, double[][] b)
        {
            if (a[0].Length != b.GetLength(0))
            {
                throw new FormatException("a's column number must be equal to b's row number");
            }

            int m = a.GetLength(0);
            int n = b[0].Length;
            int p = a[0].Length;

            double[][] result = new double[m][];

            for (int i = 0; i < m; ++i)
            {
                double[] resultrow = new double[n];
                for (int j = 0; j < n; ++j)
                {
                    //result[i][j] = 行向量 a[i] 与列向量 b[j] 的点积
                    double[] row = a[i];
                    double[] col = new double[p];
                    //取得列向量
                    for (int k = 0; k < p; ++k)
                    {
                        col[k] = b[k][j];
                    }
                    //点积
                    resultrow[j] = Dot(row, col);
                }
                result[i] = resultrow;
            }
            return result;
        }

        /// <summary>
        /// 将一个矩阵转置
        /// </summary>
        /// <param name="a">待转置的矩阵</param>
        /// <returns>返回转置后的数组</returns>
        public static double[][] Transpose(double[][] a)
        {
            double[][] trans = new double[a[0].Length][];
            for (int i = 0; i < a[0].Length; ++i)
            {
                double[] row = new double[a.GetLength(0)];
                for (int j = 0; j < a.GetLength(0); ++j)
                {
                    row[j] = a[j][i];
                }
                trans[i] = row;
            }
            return trans;
        }

        /// <summary>
        /// 计算矩阵与向量的乘积
        /// </summary>
        /// <param name="a">左乘的矩阵</param>
        /// <param name="x">列向量</param>
        /// <returns>返回一个向量</returns>
        /// <exception cref="FormatException"></exception>
        public static double[] Mult(double[][] a, double[] x)
        {
            if (a[0].Length != x.Length)
            {
                throw new FormatException("a's column number must be equal to x's length");
            }

            double[] result = new double[a.GetLength(0)];

            for (int i = 0; i < a.GetLength(0); ++i)
            {
                result[i] = Dot(a[i], x);
            }

            return result;
        }

        /// <summary>
        /// 计算向量与矩阵的乘积
        /// </summary>
        /// <param name="x">行向量</param>
        /// <param name="a">矩阵</param>
        /// <returns>返回一个向量</returns>
        /// <exception cref="FormatException"></exception>
        public static double[] Mult(double[] x, double[][] a)
        {
            if (a.GetLength(0) != x.Length)
            {
                throw new FormatException("a's column number must be equal to x's length");
            }

            double[] result = new double[a[0].Length];

            for (int i = 0; i < a[0].Length; ++i)
            {
                double[] colVector = new double[a.GetLength(0)];
                for (int j = 0; j < colVector.Length; ++j)
                {
                    colVector[j] = a[j][i];
                }
                result[i] = Dot(x, colVector);
            }

            return result;
        }

        /// <summary>
        /// 在控制台上输出矩阵
        /// </summary>
        /// <param name="a">需要输出的矩阵</param>
        public static void PrintMatrix(double[][] a)
        {
            for (int i = 0; i < a.GetLength(0); ++i)
            {
                for (int j = 0; j < a[i].Length; ++j)
                {
                    Console.Write($"	{a[i][j]}");
                }
                Console.Write("
");
            }
        }

        /// <summary>
        /// 在控制台上输出一行向量
        /// </summary>
        /// <param name="a">需要输出的向量</param>
        public static void PrintVector(double[] a)
        {
            for (int i = 0; i < a.Length; ++i)
            {
                Console.Write($"	{a[i]}");
            }
            Console.Write("
");
        }
    }

1.1.34

解答

第二个以及最后三个需要，其他都可以设计成过滤器的模式。

这里的 largeW.txt 只需要保留前 100 个数字就可以了，太多的话最后两个测试会刷屏。

代码

static void Main(string[] args)
        {
            string[] AllNumbers = File.ReadAllLines("largeW.txt");
            int N = AllNumbers.Length;
            int[] input = new int[N];

            for (int i = 0; i < N; ++i)
            {
                input[i] = int.Parse(AllNumbers[i]);
            }

            MinAndMax(input);
            Console.WriteLine();

            MidNumber(input);
            Console.WriteLine();

            NumberK(4, input);
            Console.WriteLine();

            SquareSum(input);
            Console.WriteLine();

            AboveAverage(input);
            Console.WriteLine();

            Ascending(input);
            Console.WriteLine();

            Shuffle(input);
            Console.WriteLine();
        }

        /// <summary>
        /// 获取最大值和最小值
        /// </summary>
        /// <param name="input">输入流</param>
        static void MinAndMax(int[] input)
        {
            //只用到了两个变量
            int min = input[0];
            int max = input[0];

            //只对输入值正向遍历一遍，不需要保存
            for (int i = 1; i < input.Length; ++i)
            {
                if (input[i] > max)
                {
                    max = input[i];
                }

                if (input[i] < min)
                {
                    min = input[i];
                }
            }

            Console.WriteLine("Min and Max:");
            Console.WriteLine($"Min: {min}
Max: {max}");
        }

        /// <summary>
        /// 获取中位数
        /// </summary>
        /// <param name="input">输入流</param>
        /// <returns>中位数</returns>
        static int MidNumber(int[] input)
        {
            //需要对输入值进行去重 & 排序，故需要保存
            List<int> DistinctNumbers = new List<int>(input.Distinct());
            DistinctNumbers.Sort();
            Console.WriteLine("MidNumber:");
            Console.WriteLine(DistinctNumbers[DistinctNumbers.Count / 2]);

            return DistinctNumbers[DistinctNumbers.Count / 2];
        }

        /// <summary>
        /// 获取第 k 小的数
        /// </summary>
        /// <param name="k">需要获取的排名</param>
        /// <param name="input">输入流</param>
        /// <returns>第 k 小的数</returns>
        static int NumberK (int k, int[] input)
        {
            int[] temp = new int[101];

            //只正向遍历一遍，不需要保存
            for (int i = 0; i < input.Length; ++i)
            {
                if (i < 100)
                {
                    temp[i] = input[i];
                }
                else
                {
                    temp[100] = input[i];
                    Array.Sort(temp);
                }
            }

            Console.WriteLine("NumberK");
            Console.WriteLine($"No.k: {temp[k - 1]}");

            return temp[k - 1];
        }

        /// <summary>
        /// 计算输入流中所有数的平方和
        /// </summary>
        /// <param name="input">输入流</param>
        /// <returns>所有数的平方和</returns>
        static long SquareSum(int[] input)
        {
            long sum = 0;
            //只正向遍历一遍，不需要保存
            for (int i = 0; i < input.Length; ++i)
            {
                sum += input[i] * input[i];
            }

            Console.WriteLine("Sum Of Square:");
            Console.WriteLine(sum);

            return sum;
        }

        /// <summary>
        /// 计算所有输入数据的平均值
        /// </summary>
        /// <param name="input">输入流</param>
        /// <returns>所有输入数据的平均值</returns>
        static double Average(int[] input)
        {
            long sum = 0;

            //只遍历一遍，且不保存整个数组
            for (int i = 0; i < input.Length; ++i)
            {
                sum += input[i];
            }

            double ave = sum / (double)input.Length;

            Console.WriteLine("Average:");
            Console.WriteLine(ave);

            return ave;
        }

        /// <summary>
        /// 计算大于平均值的元素数量
        /// </summary>
        /// <param name="input">输入流</param>
        /// <returns>大于平均值的元素数量</returns>
        static double AboveAverage(int[] input)
        {
            double ave = Average(input);
            Console.WriteLine();
            double count = 0;

            for (int i = 0; i < input.Length; ++i)
            {
                if (input[i] > ave)
                {
                    count++;
                }
            }


            Console.WriteLine("AboveAverage:");
            Console.WriteLine($"{(count / input.Length) * 100}%");

            return count;
        }

        /// <summary>
        /// 升序打印数组
        /// </summary>
        /// <param name="input">输入流</param>
        static void Ascending(int[] input)
        {
            Array.Sort(input);

            Console.WriteLine("Ascending:");
            for (int i = 0; i < input.Length; ++i)
            {
                Console.Write($" {input[i]}");
            }
            Console.Write("
");
        }

        /// <summary>
        /// 随机打印数组
        /// </summary>
        /// <param name="input">输入流</param>
        static void Shuffle(int[] input)
        {
            Random random = new Random();
            List<int> All = new List<int>(input);
            int N = input.Length;
            int temp = 0;

            Console.WriteLine("Shuffle:");
            for (int i = 0; i < N; ++i)
            {
                temp = random.Next(0, All.Count - 1);
                Console.Write($" {All[temp]}");
                All.RemoveAt(temp);
            }
        }

实验题（1.1.35~1.1.39）

1.1.35

解答

这里用 Random 类模拟掷骰子并计算概率，最后和程序得出的比较。

代码

//程序运行大概需要十几秒时间（也可能更长，看运气）
        //我的数据：
        //24098 44448 37776 44401 32541
        static void Main(string[] args)
        {
            //书中给出的程序
            int SIDES = 6;
            double[] dist = new double[2 * SIDES + 1];
            for (int i = 1; i <= SIDES; i++)
                for (int j = 1; j <= SIDES; j++)
                    dist[i + j] += 1.0;

            for (int k = 2; k <= 2 * SIDES; k++)
                dist[k] /= 36.0;

            //不断进行模拟，直至误差小于 0.001
            int N = 36;
            bool isAccepted = false;
            double[] disttemp = null;
            double error = 0.001;
            while (isAccepted == false)
            {
                disttemp = PlayDice(N);
                isAccepted = true;
                for (int i = 0; i < disttemp.Length; ++i)
                {
                    if (Math.Abs(disttemp[i] - dist[i]) >= error)
                        isAccepted = false;
                }
                N++;
            }

            Console.WriteLine($"N:{N}
");
            for (int i = 0; i < dist.Length; ++i)
            {
                Console.WriteLine($"{i}:
 Standerd:{dist[i]}
Simulated:{disttemp[i]}
Offset:{Math.Abs(disttemp[i] - dist[i])}");
            }
        }

        //利用随机数模拟掷骰子
        static double[] PlayDice(int N)
        {
            Random random = new Random();

            int SIDES = 6;
            double[] dist = new double[2 * SIDES + 1];

            //掷 N 次
            int sumtemp = 0;
            for (int i = 0; i < N; ++i)
            {
                sumtemp = random.Next(1, 7) + random.Next(1, 7);
                dist[sumtemp]++;
            }

            //计算概率
            for (int i = 0; i < dist.Length; ++i)
            {
                dist[i] /= N;
            }

            return dist;
        }

1.1.36

解答

N 取到 1000 左右数据就比较明显了。

N = 1000， M = 10

代码

static void Main(string[] args)
        {
            int M = 10;//数组大小
            int N = 1000;//打乱次数
            int[] a = new int[10];

            int[,] result = new int[M, M];

            for (int i = 0; i < N; ++i)
            {
                //初始化
                for (int j = 0; j < a.Length; ++j)
                {
                    a[j] = j;
                }

                //打乱
                Shuffle(a, i);

                //记录
                for (int j = 0; j < M; ++j)
                {
                    result[a[j], j]++;
                }
            }

            PrintMatrix(result);
        }

        /// <summary>
        /// 打乱数组
        /// </summary>
        /// <param name="a">需要打乱的数组</param>
        /// <param name="seed">用于生成随机数的种子值</param>
        static void Shuffle(int[] a, int seed)
        {
            int N = a.Length;
            Random random = new Random(seed);
            for (int i = 0; i < N; ++i)
            {
                int r = i + random.Next(N - i);//等于StdRandom.uniform(N-i)
                int temp = a[i];
                a[i] = a[r];
                a[r] = temp;
            }
        }

        /// <summary>
        /// 在控制台上输出矩阵
        /// </summary>
        /// <param name="a">需要输出的矩阵</param>
        public static void PrintMatrix(int[,] a)
        {
            for (int i = 0; i < a.GetLength(0); ++i)
            {
                for (int j = 0; j < a.GetLength(1); ++j)
                {
                    Console.Write($"	{a[i,j]}");
                }
                Console.Write("
");
            }
        }

1.1.37

解答

使用 0~N-1 的随机数会导致每次交换的数字可能相同。
例如：
原数组： 1 2 3 4。
第一次： 2 1 3 4 random = 1，第 0 个和第 1 个交换。
第二次： 1 2 3 4 random = 0，第 1 个和第 0 个交换。

代码

static void Main(string[] args)
        {
            int M = 10;//数组大小
            int N = 100000;//打乱次数
            int[] a = new int[10];

            int[,] result = new int[M, M];

            for (int i = 0; i < N; ++i)
            {
                //初始化
                for (int j = 0; j < a.Length; ++j)
                {
                    a[j] = j;
                }

                //打乱
                Shuffle(a, i);

                //记录
                for (int j = 0; j < M; ++j)
                {
                    result[a[j], j]++;
                }
            }

            PrintMatrix(result);
        }

        /// <summary>
        /// 打乱数组（不够好的版本）
        /// </summary>
        /// <param name="a">需要打乱的数组</param>
        /// <param name="seed">用于生成随机数的种子值</param>
        static void Shuffle(int[] a, int seed)
        {
            int N = a.Length;
            Random random = new Random(seed);
            for (int i = 0; i < N; ++i)
            {
                //int r = i + random.Next(N - i);
                int r = random.Next(N); //返回的是 0 ~ N-1 之间的随机整数
                int temp = a[i];
                a[i] = a[r];
                a[r] = temp;
            }
        }

        /// <summary>
        /// 在控制台上输出矩阵
        /// </summary>
        /// <param name="a">需要输出的矩阵</param>
        public static void PrintMatrix(int[,] a)
        {
            for (int i = 0; i < a.GetLength(0); ++i)
            {
                for (int j = 0; j < a.GetLength(1); ++j)
                {
                    Console.Write($"	{a[i, j]}");
                }
                Console.Write("
");
            }
        }

1.1.38

解答

为了使差距比较明显，故意取了比较靠后的数字。

代码

static void Main(string[] args)
        {
            string[] largeWString = File.ReadAllLines("largeW.txt");
            int[] largeW = new int[largeWString.Length];
            for (int i = 0; i < largeW.Length; ++i)
            {
                largeW[i] = int.Parse(largeWString[i]);
            }
            Stopwatch timer = Stopwatch.StartNew();
            BruteForceSearch(111111, largeW);
            Console.WriteLine($"BruteForceSearch: {timer.ElapsedMilliseconds} ms");

            timer.Restart();
            rank(111111, largeW);
            Console.WriteLine($"BinarySearch: {timer.ElapsedMilliseconds} ms");

            string[] largeTString = File.ReadAllLines("largeT.txt");
            int[] largeT = new int[largeTString.Length];
            for (int i = 0; i < largeW.Length; ++i)
            {
                largeT[i] = int.Parse(largeTString[i]);
            }

            timer.Restart();
            BruteForceSearch(111111, largeT);
            Console.WriteLine($"BruteForceSearch: {timer.ElapsedMilliseconds} ms");

            timer.Restart();
            rank(111111, largeT);
            Console.WriteLine($"BinarySearch: {timer.ElapsedMilliseconds} ms");
        }

        //暴力查找
        public static int BruteForceSearch(int key, int[] a)
        {
            for (int i = 0; i < a.Length; ++i)
            {
                if (a[i] == key)
                    return i;
            }

            return -1;
        }

        //重载方法，用于启动二分查找
        public static int rank(int key, int[] a)
        {
            return rank(key, a, 0, a.Length - 1, 1);
        }

        //二分查找
        public static int rank(int key, int[] a, int lo, int hi, int number)
        {
            if (lo > hi)
            {
                return -1;
            }

            int mid = lo + (hi - lo) / 2;

            if (key < a[mid])
            {
                return rank(key, a, lo, mid - 1, number + 1);
            }
            else if (key > a[mid])
            {
                return rank(key, a, mid + 1, hi, number + 1);
            }
            else
            {
                return mid;
            }
        }

1.1.39

解答

按照要求编程就好，视机器不同需要的时间也不同。

代码

//需要 6 秒左右的运算时间
        static void Main(string[] args)
        {
            Random r = new Random();
            int baseNum = 10;
            int powNum = 3;
            int T = 10;
            int M = 4;

            double[,] Matrix = new double[M,2];

            for (int i = 0; i < M; ++i)
            {
                int N = (int)Math.Pow(baseNum, powNum + i);
                double sum = 0;
                for (int j = 0; j < T; ++j)
                {
                    sum += Test(N, r.Next());
                }
                Matrix[i, 0] = N;
                Matrix[i, 1] = sum / T;
            }

            PrintMatrix(Matrix);
        }

        /// <summary>
        /// 执行一次“实验”
        /// </summary>
        /// <param name="N">数组的大小</param>
        /// <param name="seed">随机种子</param>
        /// <returns>返回相同数字的数目</returns>
        static int Test(int N, int seed)
        {
            Random random = new Random(seed);
            int[] a = new int[N];
            int[] b = new int[N];
            int count = 0;

            for (int i = 0; i < N; ++i)
            {
                a[i] = random.Next(100000, 1000000);
                b[i] = random.Next(100000, 1000000);
            }

            for (int i = 0; i < N; ++i)
            {
                if (rank(a[i], b) != -1)
                    count++;
            }

            return count;
        }

        //重载方法，用于启动二分查找
        public static int rank(int key, int[] a)
        {
            return rank(key, a, 0, a.Length - 1, 1);
        }

        //二分查找
        public static int rank(int key, int[] a, int lo, int hi, int number)
        {
            if (lo > hi)
            {
                return -1;
            }

            int mid = lo + (hi - lo) / 2;

            if (key < a[mid])
            {
                return rank(key, a, lo, mid - 1, number + 1);
            }
            else if (key > a[mid])
            {
                return rank(key, a, mid + 1, hi, number + 1);
            }
            else
            {
                return mid;
            }
        }

        /// <summary>
        /// 在控制台上输出矩阵
        /// </summary>
        /// <param name="a">需要输出的矩阵</param>
        public static void PrintMatrix(double[,] a)
        {
            for (int i = 0; i < a.GetLength(0); ++i)
            {
                for (int j = 0; j < a.GetLength(1); ++j)
                {
                    Console.Write($"	{a[i, j]}");
                }
                Console.Write("
");
            }
        }