线段树学习资料

前言：

本来决定学完数据结构就去学习的东西，结果一直咕到现在。。

线段树是一种高级数据结构。

是一种二叉树，也就是对于一个线段，我们会用一个二叉树来表示。

正文：

线段树可以做单点查询，单点修改，区间查询，区间修改......

一般线段树都是

我们来举个例子

现在我有这么一串数字：

把他放入一棵线段树中，就变成这样了：

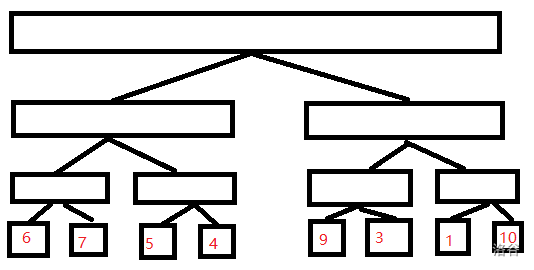
然后每个叶子节点的父亲都是他的儿子的值的和，这就是一棵普通的线段树：

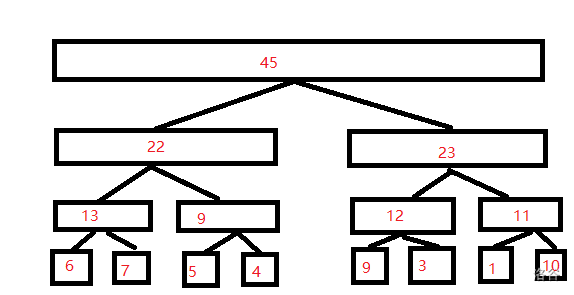
我们把每一个节点都按顺序标上序号：

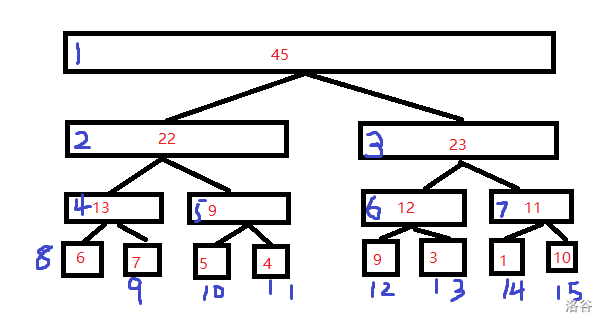
我们发现，每个节点的儿子的序号和它本身的序号是有关系的----它本身的序号是a，左儿子的序号2a，而右儿子的序号是2a+1。
所以，我们就可以递归的从下往上造一棵线段树。

定义

int input[500005];//用来存放输入的数组。
struct node{
    int l,r,sum;//l和r分别表示当前节点表示的范围，sum是这个节点的值。
}tree[4*500005];//线段树的空间要开到原数组的4倍，否则会死的很惨。

建树

void build(int i,int l,int r){//递归建树，一般来说，调用的时候，i的位置填1，l和r分别填输入的数组的第一个序号和最后一个序号。
   tree[i].l=l;tree[i].r=r;
   if(l==r){//如果这个节点是叶子节点
       tree[i].sum=input[l];
       return ;
   }
   int mid=(l+r)>>1;
   build(i*2,l,mid);
   build(i*2+1,mid+1,r);//分别构造左子树和右子树
   tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//然后由儿子推到父亲。
	return ;
}

接下来我们来学习一些基本操作

区间修改

如果这个区间被完全包括在目标区间里面，讲这个区间标记k

代码

inline void add(int i,int l,int r,int k){
    if(tree[i].l>=l && tree[i].r<=r){//如果这个区间被完全包括在目标区间里面，讲这个区间标记k
        tree[i].sum+=k;
        return ;
    }
    if(tree[i*2].r>=l)
        add(i*2,l,r,k);
    if(tree[i*2+1].l<=r)
        add(i*2+1,l,r,k);
}

单点查询

所谓单点查询，就是在一顿加加减减的操作后问你第*个数当前的值是多少。

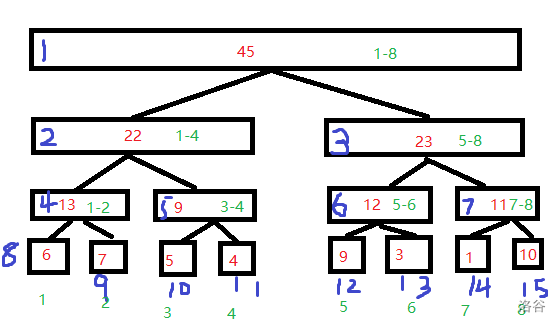
就在这张图上，举个例子：我现在想知道第5个数的数值。

于是就产生了如下的搜索

搜索是根据节点的范围来判断的，如果正好是这个节点，就直接输出。如果被包含在这个节点里，就继续细化。

代码

void search(int i,int dis){
    if(tree[i].l==tree[i].r) {
    	 return tree[i].sum;
	}
	int mid=(tree[i].l+tree[i].r)/2;
    if(dis<=mid) return search(i*2,dis);
    else return search(i*2+1,dis);
}

---------------------------------------------------分割线------------------------------------------------------------------------------

区间查询

和单点查询差不多，可以理解成（有范围的）单点的查询。有些节点正好包含这一个区间，就可以直接加上去。

代码

int search(int i,int l,int r){
    if(tree[i].l>=l&&tree[i].r<=r)
        return tree[i].sum;
    if(tree[i].r<l||tree[i].l>r) return 0;
    int s=0;
    if(tree[i*2].r>=1) s+=search(i*2,l,r);
    if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
    return s;
}

单点修改

我们建树是从下往上建，单点修改的时候则是从上往下修改，只要包含目标点的节点都加上一个同样的数，就可以了。

代码

inline void add(int i,int dis,int k){
    if(tree[i].l==tree[i].r){
        tree[i].sum+=k;
        return;
    }
    if(dis<=tree[i*2].r&&dis>=tree[i*2].l) tree[i].sum+=k,add(i*2,dis,k);
    else if(dis<=tree[i*2+1].r&&dis>=tree[i*2+1].l) tree[i].sum+=k,add(i*2+1,dis,k);
}

注意：上面的区间修改和区间查询不能共用，看下去你会知道原因

现在我们要实现间修改和区间查询。如果用把上面的2个拼起来就会出现一个问题，当要查询的区间没有完全包含在修改过的区间中，就会出现问题，所以我们需要用到懒标记。

原理：当出现上面的情况时，则先下传懒标记，再进行判断。

代码（即线段树模板题1的代码）

void pushdown(ll i){
	if(tree[i].lazy!=0){
		tree[i*2].lazy+=tree[i].lazy;
		tree[i*2+1].lazy+=tree[i].lazy;
		ll mid=(tree[i].l+tree[i].r)/2;
		tree[i*2].num+=tree[i].lazy*(mid-tree[i*2].l+1);
		tree[i*2+1].num+=tree[i].lazy*(tree[i*2+1].r-mid);
		tree[i].lazy=0;
	}
	return ;
}
void add(ll i,ll l,ll r,ll k){
	if(tree[i].r<=r&&tree[i].l>=l) {
		tree[i].num+=k*(tree[i].r-tree[i].l+1);
		tree[i].lazy+=k;
		return;
	}
	pushdown(i);
	if(tree[i*2].r>=l)
		add(i*2,l,r,k);
	if(tree[i*2+1].l<=r)
		add(i*2+1,l,r,k);
	tree[i].num=tree[i*2].num+tree[i*2+1].num;
	return;
} 

ll search(ll i,ll l,ll r)
{
	if(tree[i].l>=l && tree[i].r<=r)
	return tree[i].num;
	if(tree[i].r<l||tree[i].l>r) return 0;
	pushdown(i);
	ll s=0;
	if(tree[i*2].r>=l) s+=search(i*2,l,r);
	if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
	return s; 
}

在线段树模板2中出现了乘法

这时候，不能像加法一样做了，因为运算符不同，运算的顺序也是不一样的。

这就要当懒标记下标传递的时候，我们需要考虑，是先加再乘还是先乘再加。我们只需要对懒标记做这样一个处理。

懒标记分为两种，分别是加法的plz和乘法的mlz。

代码和上面相似，多了一个函数

（线段树模板题2）代码

 void pushdown(ll i){
    ll k1=tree[i].mlz,k2=tree[i].plz;
    tree[i<<1].sum=(tree[i<<1].sum*k1+k2*(tree[i<<1].r-tree[i<<1].l+1))%p;
    tree[i<<1|1].sum=(tree[i<<1|1].sum*k1+k2*(tree[i<<1|1].r-tree[i<<1|1].l+1))%p;
    tree[i<<1].mlz=(tree[i<<1].mlz*k1)%p;
    tree[i<<1|1].mlz=(tree[i<<1|1].mlz*k1)%p;
    tree[i<<1].plz=(tree[i<<1].plz*k1+k2)%p;
    tree[i<<1|1].plz=(tree[i<<1|1].plz*k1+k2)%p;
    tree[i].plz=0;
    tree[i].mlz=1;
    return ;
}
inline void mul(ll i,ll l,ll r,ll k){
    if(tree[i].r<l || tree[i].l>r)  return ;
    if(tree[i].l>=l && tree[i].r<=r){
        tree[i].sum=(tree[i].sum*k)%p;
        tree[i].mlz=(tree[i].mlz*k)%p;
        tree[i].plz=(tree[i].plz*k)%p;
        return ;
    }
    pushdown(i);
    if(tree[i<<1].r>=l)  mul(i<<1,l,r,k);
    if(tree[i<<1|1].l<=r)  mul(i<<1|1,l,r,k);
    tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
    return ;
}
void add(ll i,ll l,ll r,ll k){
    if(tree[i].r<l || tree[i].l>r)  return ;
    if(tree[i].l>=l && tree[i].r<=r){
        tree[i].sum+=((tree[i].r-tree[i].l+1)*k)%p;
        tree[i].plz=(tree[i].plz+k)%p;
        return ;
    }
    pushdown(i);
    if(tree[i<<1].r>=l)  add(i<<1,l,r,k);
    if(tree[i<<1|1].l<=r)  add(i<<1|1,l,r,k);
    tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
    return ;
}
ll search(ll i,ll l,ll r){
    if(tree[i].r<l || tree[i].l>r)  return 0;
    if(tree[i].l>=l && tree[i].r<=r)
        return tree[i].sum;
    pushdown(i);
    ll sum=0;
    if(tree[i<<1].r>=l)  sum+=search(i<<1,l,r)%p;
    if(tree[i<<1|1].l<=r)  sum+=search(i<<1|1,l,r)%p;
    return sum%p;
}

最后把4道模板题的代码都放一下

【模板】树状数组 1

#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x) {
    x = 0;
    int f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + (ch ^ 48);
        ch = getchar();
    }
    x *= f;
    return;
}
template <typename T>
inline void write(T x)
{
    if(x < 0) {
        putchar('-');
        x = -x;
    }
    if(x > 9)
        write(x/10);
    putchar(x % 10 + '0');
    return;
}
int n,m,p;
int input[500005];
struct node{
    int l,r,sum;
}tree[4*500005];
inline void build(int i,int l,int r){
    tree[i].l=l,tree[i].r=r;
    if(l==r){
        tree[i].sum=input[l];
        return;
    }
    int mid=(l+r)>>1;
    build(i*2,l,mid);build(i*2+1,mid+1,r);
    tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
    return;
}
inline int search(int i,int l,int r){
    if(tree[i].l>=l&&tree[i].r<=r)
        return tree[i].sum;
    if(tree[i].r<l||tree[i].l>r) return 0;
    int s=0;
    if(tree[i*2].r>=1) s+=search(i*2,l,r);
    if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
    return s;
}
inline void add(int i,int dis,int k){
    if(tree[i].l==tree[i].r){
        tree[i].sum+=k;
        return;
    }
    if(dis<=tree[i*2].r) add(i*2,dis,k);
    else add(i*2+1,dis,k);
    tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
}

int main(){
    int a,b,c,d;
    read(n),read(m);
    for(int i=1;i<=n;i++)
        read(input[i]);
    build(1,1,n);
    for(int i=1;i<=m;i++){
        read(a),read(b),read(c);
        if(a==1){
            add(1,b,c);
        }
        else{
            write(search(1,b,c)),cout<<endl;
        }
    }
}

【模板】树状数组 2

#include<bits/stdc++.h>
using namespace std;
template <typename T>
void read(T &x) {
    x = 0;
    int f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + (ch ^ 48);
        ch = getchar();
    }
    x *= f;
    return;
}
template <typename T>
void write(T x)
{
    if(x < 0) {
        putchar('-');
        x = -x;
    }
    if(x > 9)
        write(x/10);
    putchar(x % 10 + '0');
    return;
}

int n,m,a,b,c,ans,f;
struct Tree{
	int l,r,num;
}tree[500005*4]; 
int input[500005];
inline void build(int i,int l,int r){
	tree[i].l=l,tree[i].r=r;
	if(l==r){
		tree[i].num=input[l];
		return;
	}
	int mid=(l+r)/2;
	build(i*2,l,mid);build(i*2+1,mid+1,r);
	tree[i].num=tree[i*2].num+tree[i*2+1].num;
}

inline void add(int i,int l,int r,int k)
{
	if(tree[i].l>=l&&tree[i].r<=r){
        tree[i].num+=k;
        return;
    }
    if(tree[i*2].r>=l)
        add(i*2,l,r,k);
    if(tree[i*2+1].l<=r)
        add(i*2+1,l,r,k);
}
inline void search(int i,int dis){//此处的代码和上文讲的不太一样，都可以。
	ans+=tree[i].num;
    if(tree[i].l==tree[i].r) {
    	 return ;
	}
	int mid=(tree[i].l+tree[i].r)/2;
    if(dis<=mid) search(i*2,dis);
    if(dis>mid) search(i*2+1,dis);
}
int main(){
    read(n),read(m);
	build(1,1,n);
    for(int i=1;i<=n;i++)
        read(input[i]);
    for(int i=1;i<=m;i++)
    {
        read(f);
        if(f==1){
            read(a),read(b),read(c);
            add(1,a,b,c);
        }
        else{
            ans=0;
            read(a);
            search(1,a);
            cout<<ans+input[a]<<endl;
        }
        
    }
}

【模板】线段树 1

#include<bits/stdc++.h>
#define ll long long
using namespace std;

template <typename T>
inline void read(T &x) {
    x = 0;
    ll f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = x * 10 + (ch ^ 48);
        ch = getchar();
    }
    x *= f;
    return;}
template <typename T>
inline void write(T x){
    if(x < 0) {
        putchar('-');
        x = -x;
    }
    if(x > 9)
        write(x/10);
    putchar(x % 10 + '0');
    return;
}

ll n,m,input[500005],a,b,c,d;
struct Tree{
	ll l,r,num,lazy;
}tree[500005*4];
inline void build(ll i,ll l,ll r){
	tree[i].l=l,tree[i].r=r;
	if(l==r){
		tree[i].num=input[l];
		return;
	}
	ll mid=(l+r)/2;
	build(i*2,l,mid);
	build(i*2+1,mid+1,r);
	tree[i].num=tree[i*2].num+tree[i*2+1].num;
}
inline void pushdown(ll i){
	if(tree[i].lazy!=0){
		tree[i*2].lazy+=tree[i].lazy;
		tree[i*2+1].lazy+=tree[i].lazy;
		ll mid=(tree[i].l+tree[i].r)/2;
		tree[i*2].num+=tree[i].lazy*(mid-tree[i*2].l+1);
		tree[i*2+1].num+=tree[i].lazy*(tree[i*2+1].r-mid);
		tree[i].lazy=0;
	}
	return ;
}
inline void add(ll i,ll l,ll r,ll k){
	if(tree[i].r<=r&&tree[i].l>=l) {
		tree[i].num+=k*(tree[i].r-tree[i].l+1);
		tree[i].lazy+=k;
		return;
	}
	pushdown(i);
	if(tree[i*2].r>=l)
		add(i*2,l,r,k);
	if(tree[i*2+1].l<=r)
		add(i*2+1,l,r,k);
	tree[i].num=tree[i*2].num+tree[i*2+1].num;
	return;
} 

inline ll search(ll i,ll l,ll r)
{
	if(tree[i].l>=l && tree[i].r<=r)
	return tree[i].num;
	if(tree[i].r<l||tree[i].l>r) return 0;
	pushdown(i);
	ll s=0;
	if(tree[i*2].r>=l) s+=search(i*2,l,r);
	if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
	return s; 
}
int main(){
    read(n),read(m);
    for(register ll i=1;i<=n;i++)	
    	read(input[i]);
    build(1,1,n);
    for(register ll i=1;i<=m;i++){
		read(d);
		if(d==1) read(a),read(b),read(c),add(1,a,b,c);
		else read(a),read(b),write(search(1,a,b)),cout<<'\n';
	}
} 

【模板】线段树 2

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,p;
ll input[100010];
struct node{
    ll l,r;
    ll sum,mlz,plz;
}tree[4*100010];
inline void build(ll i,ll l,ll r){
    tree[i].l=l;
    tree[i].r=r;
    tree[i].mlz=1;
    if(l==r){
        tree[i].sum=input[l]%p;
        return ;
    }
    ll mid=(l+r)>>1;
    build(i<<1,l,mid);
    build(i<<1|1,mid+1,r);
    tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
    return ;
}
inline void pushdown(ll i){
    ll k1=tree[i].mlz,k2=tree[i].plz;
    tree[i<<1].sum=(tree[i<<1].sum*k1+k2*(tree[i<<1].r-tree[i<<1].l+1))%p;
    tree[i<<1|1].sum=(tree[i<<1|1].sum*k1+k2*(tree[i<<1|1].r-tree[i<<1|1].l+1))%p;
    tree[i<<1].mlz=(tree[i<<1].mlz*k1)%p;
    tree[i<<1|1].mlz=(tree[i<<1|1].mlz*k1)%p;
    tree[i<<1].plz=(tree[i<<1].plz*k1+k2)%p;
    tree[i<<1|1].plz=(tree[i<<1|1].plz*k1+k2)%p;
    tree[i].plz=0;
    tree[i].mlz=1;
    return ;
}
inline void mul(ll i,ll l,ll r,ll k){
    if(tree[i].r<l || tree[i].l>r)  return ;
    if(tree[i].l>=l && tree[i].r<=r){
        tree[i].sum=(tree[i].sum*k)%p;
        tree[i].mlz=(tree[i].mlz*k)%p;
        tree[i].plz=(tree[i].plz*k)%p;
        return ;
    }
    pushdown(i);
    if(tree[i<<1].r>=l)  mul(i<<1,l,r,k);
    if(tree[i<<1|1].l<=r)  mul(i<<1|1,l,r,k);
    tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
    return ;
}
inline void add(ll i,ll l,ll r,ll k){
    if(tree[i].r<l || tree[i].l>r)  return ;
    if(tree[i].l>=l && tree[i].r<=r){
        tree[i].sum+=((tree[i].r-tree[i].l+1)*k)%p;
        tree[i].plz=(tree[i].plz+k)%p;
        return ;
    }
    pushdown(i);
    if(tree[i<<1].r>=l)  add(i<<1,l,r,k);
    if(tree[i<<1|1].l<=r)  add(i<<1|1,l,r,k);
    tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
    return ;
}
inline ll search(ll i,ll l,ll r){
    if(tree[i].r<l || tree[i].l>r)  return 0;
    if(tree[i].l>=l && tree[i].r<=r)
        return tree[i].sum;
    pushdown(i);
    ll sum=0;
    if(tree[i<<1].r>=l)  sum+=search(i<<1,l,r)%p;
    if(tree[i<<1|1].l<=r)  sum+=search(i<<1|1,l,r)%p;
    return sum%p;
}
int main(){
    scanf("%lld%lld%lld",&n,&m,&p);
    for(int i=1;i<=n;i++)  scanf("%lld",&input[i]);
    build(1,1,n); 
    for(int i=1;i<=m;i++){
        ll f1,a,b,c;
        scanf("%lld",&f1);
        if(f1==1)
            scanf("%lld%lld%lld",&a,&b,&c),mul(1,a,b,c);
        if(f1==2)
            scanf("%lld%lld%lld",&a,&b,&c),add(1,a,b,c);
        if(f1==3)
            scanf("%lld%lld",&a,&b),printf("%lld\n",search(1,a,b));
    }
    return 0;
}