ctr预估简单的解释就是预测用户的点击item的概率。为什么一个回归的问题需要使用分类的方法来评估,这真是一个好问题,尝试从下面几个关键问题去回答。
1、ctr预估是特殊的回归问题
ctr预估的目标函数为
f(x)=P(+1|x)
特殊之处在于目标函数的值域为[0,1],而且由于是条件概率,具有如下特性
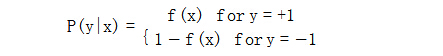
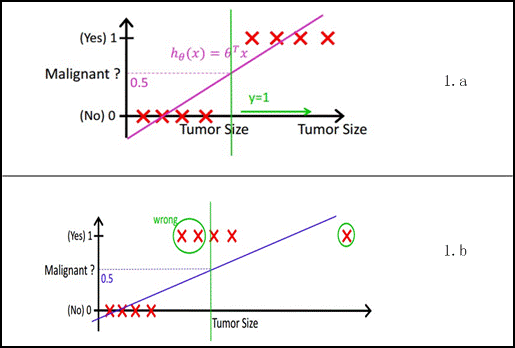
如果将ctr预估按照一般的回归问题处理(如使用Linear Regression),面临的问题是一般的linear regression的值域范围是实数域,对于整个实数域的敏感程度是相同的,所以直接使用一般的linear regression来建立ctr预估模型很容易受到noise的影响。以Andrew Ng课程中的例子图1.b所示,增加一个噪音点后,拟合的直线马上偏移。另外,由于目标函数是条件概率,训练样本中会存在特征x完全相同,y为+1和-1的样本都出现的问题,在linear regression看来是一个矛盾的问题,而Logistics Regression很好的解决了这个问题[1]。
2、LR模型的cost function不使用平方差
一般回归问题采用的cost function是预测值和实际值的平方差,而LR模型无法采用平方差作为cost function的原因是由于基于LR模型公式的平方差函数是非凸函数,无法方便的获得全局最优解。
LR模型采用的cost function是采用cross-entropy error function(也有叫做对数似然函数的),error measure是模型假设h产生训练样本D的可能性(likelihood)[2]。
假设y1=+1, y2=-1, ......., yn=-1,对应的likelihood为:


3、为什么AUC也可以用于LR模型的评估
普遍上对于AUC的认识是在分类问题中,取不同的threshold后,在横坐标false positive rate,纵坐标为true positive rate平面上绘制ROC曲线的曲线下面积,所以很难理解是如何与这里的回归问题联系起来。实际上,一个关于AUC的很有趣的性质是:它和Wilcoxon-Mann-Witney Test是等价的[3]。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本,正类样本的score有多大的概率大于负类样本的score。有了这个定义,我们就得到了另外一种计算AUC的方法:具体来说就算统计一下所有M*N(M为正类样本的数目,N为负类样本的数目)个正负样本对中,有多少个组中的正样本的score大于负样本的score。

参考文献
[1]逻辑回归模型(Logistic Regression, LR)基础。 http://www.cnblogs.com/sparkwen/p/3441197.html
[2] Machine Learning Foundation, Coursera.
[3]AUC(Area Under roc Curve )计算及其与ROC的关系 http://www.cnblogs.com/guolei/archive/2013/05/23/3095747.html