【题解】 「联合省选 2020 B」丁香之路 欧拉回路+最小生成树+贪心

Legend

Link ( extrm{to LOJ})。

Editorial

因为 siqi 哥哥出过一道欧拉回路的神仙题，所以说一下来就看出来是欧拉回路了呢！

如何判断无向图欧拉回路存在？每个点度数都是偶数且是连通图。

容易发现，题目即回答 (q) 组询问：增加边 ((s,i) (1 le i le n)) 后，再增加若干边，使得图存在欧拉回路。

并使得增加的边权尽量少。

注意到没有连边的点没必要考虑进来。

---

不难发现奇数度数的结点有偶数个，我们按大小两两贪心配对连接即可。

但这还不够，原因是可能图不联通。我们还需要把图连起来。

我们化用之前的方法，加上并查集，按编号贪心连接（获得 60分 WA）

为什么这个做法会错呢？我找到一组简易 HACK 数据：

(s=1,i=5) 时，按照上述算法会连出左图，正解是右图：

---

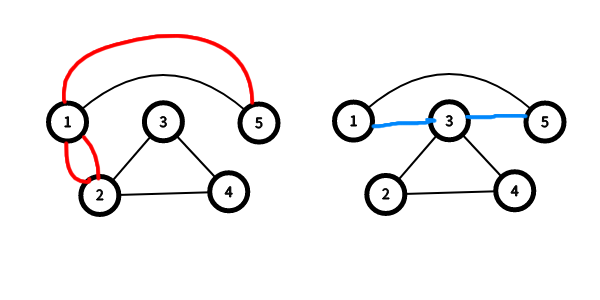
解决方法如下：

发现由于 ((i,j) (i < j)) 的边权是 (|i-j|)，((i,i+1),(i+1,i+2),cdots,(j-1,j)) 的边权和也是 (|j-i|)。

所以新增一条 ((i,j)) 边等价于连接了 ((i,i+1),(i+1,i+2),cdots,(j-1,j))。

并且这第二种方式没有改变 (i+1,i+2,cdots,j-1) 的度数奇偶性，还能连接更多的联通块，这是非常好的。

最后剩余还没有连接的联通块，也就只能贪心最小生成树了。

注意到可能成为最小生成树的边 ((l_1,r_1))，((l_2,r_2)) 如果看成区间一定不会出现相交的情况。

即最多只有 (O(n)) 条边参与生成树。

于是对每一组询问均运行此算法：复杂度 (O(n^2 log n))。

用桶代替排序，将并查集加上按秩合并和路径压缩，复杂度可以优化为 (O(n^2 alpha(n)))。

Editorial

int n, m, s, d[MX], FF[MX], fa[MX], sz[MX] ,hav[MX] ,SZ[MX];
void init() {
    for (int i = 1 ; i < MX ; ++i)
        FF[i] = fa[i] = i;
}
int find1(int x) {return FF[x] == x ? x : FF[x] = find1(FF[x]);}
void link1(int x, int y) {x = find1(x), y = find1(y), FF[x] = y;}
int find(int x) {return fa[x] == x ? x : fa[x] = find(fa[x]);}
void link(int x, int y) {
    x = find(x), y = find(y);

    if (x == y) return;

    if (sz[x] < sz[y])
        std::swap(x, y);
    sz[x] += sz[y], fa[y] = x;
}

LL ans;

struct edge {
    int u, v, w;
    bool operator <(const edge &B)const {
        return w < B.w;
    }
} e[MX];

int main() {
	__FILE([省选联考2020B卷]丁香之路);
    init();
    n = read(), m = read(), s = read();

    for (int i = 1, u, v ; i <= m ; ++i) {
        u = read(), v = read();
		++hav[u] ,++hav[v];
        link1(u, v);
        ans += std::abs(u - v);
        d[u] ^= 1, d[v] ^= 1;
    }

    for (int i = 1 ; i <= n ; ++i) find1(i);

    memcpy(fa, FF, sizeof fa);
	memcpy(SZ ,sz ,sizeof sz);

	++hav[s];
	d[s] ^= 1;
    for (int i = 1 ; i <= n ; ++i) {
		debug("%d
" ,i);
		memcpy(fa ,FF ,sizeof fa);
		memcpy(sz ,SZ ,sizeof sz);
        link(s, i);
		++hav[i];
        d[i] ^= 1;
        int tmp = 0;

        for (int j = 1, las = 0 ; j <= n ; ++j) {
            if (!d[j]) continue;
            if (las) {
                int fdj = find(j);
                tmp += j - las;
                link(fdj, las);

                for (++las ; las < j ; ++las) {
                    int k = find(las);
                    link(k, fdj);
                }
                las = 0;
            } else las = j;
        }

        d[i] ^= 1;
        int ecnt = 0;

        for (int j = 1, las = 0 ; j <= n ; ++j) {
            if (!hav[j]) continue;
            if (las) {
                if (find(j) != find(las)) {
                    e[++ecnt] = (edge) { j, las, (j - las) * 2 };
                }
            }
            las = j;
        }
        std::sort(e + 1, e + 1 + ecnt);

        for (int j = 1, u, v ; j <= ecnt ; ++j) {
            u = find(e[j].u), v = find(e[j].v);
            if (u == v) continue;
            tmp += e[j].w;
            link(u, v);
        }
		--hav[i];
        printf("%lld%c", ans + tmp, " 
"[i == n]);
    }

    return 0;
}