数据流中位数 · data stream median

［抄题］：

数字是不断进入数组的，在每次添加一个新的数进入数组的同时返回当前新数组的中位数。

［思维问题］：

［一句话思路］：

左边x个元素，右边要有x+1个元素，因此利用maxheap把左边的最大值揪出来，利用minheap把右边的最小值揪出来

如果maxHeap.peek() > minHeap.peek()，就不断流动，直到顺滑。

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

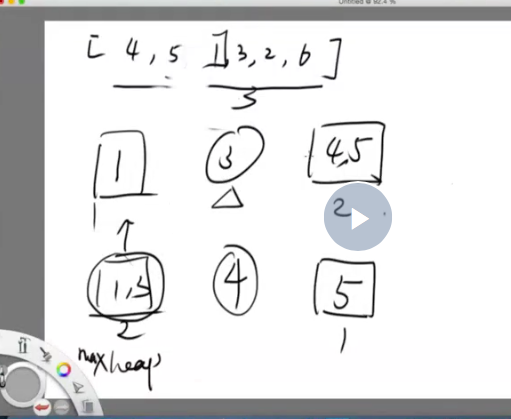
［一刷］：

1. 接口类是Queue<Integer>，指明里面的数据类型
2. compare类无参数，里面的方法有参数
3. maxheap也有参数，是cnt,cpr，因为要用到比较
   
4. 这道题要求的是 不断添加之后，返回一个ans［］

［二刷］：

1.  如果minHeap.isEmpty()，才需要讲总元素个数加一
2. MinHeap,MaxHeap,numOfElements都是几个函数公用的数据结构，要声明为private类型后放在外面

［三刷］：

［四刷］：

［五刷］：

［总结］：

［复杂度］：Time complexity: O(n个数＊add的lgn） Space complexity: O(n)

［英文数据结构，为什么不用别的数据结构］：

［其他解法］：

［Follow Up］：

［题目变变变］：

public class Solution {
    /*
     * @param nums: A list of integers
     * @return: the median of numbers
     */
     private Queue<Integer> MinHeap,MaxHeap;
     private int numOfElements = 0;
     
    public int[] medianII(int[] nums) {
        int cnt = nums.length;
        Comparator<Integer> revcmp = new Comparator<Integer>() {
            public int compare(Integer left,Integer right) {
                return right.compareTo(left);
            }
        };
        MinHeap = new PriorityQueue<Integer>(cnt);
        MaxHeap = new PriorityQueue<Integer>(cnt,revcmp);
        int[] ans = new int[cnt];
        for (int i = 0; i < cnt; i++) {
            addNumber(nums[i]);
            ans[i] = getMedian();
        }
        return ans;
    }
    
    //addNumber
    private void addNumber(int value) {
        MaxHeap.add(value);
        if (numOfElements % 2 == 0) {
            if (MinHeap.isEmpty()) {
                numOfElements = 1;
                return ;
            }
            else if (MaxHeap.peek() > MinHeap.peek()) {
                int root_Of_MaxHeap = MaxHeap.poll();
                int root_Of_MinHeap = MinHeap.poll();
                MaxHeap.add(root_Of_MinHeap);
                MinHeap.add(root_Of_MaxHeap);
            }
        }
        else {
            MinHeap.add(MaxHeap.poll());
        }
        numOfElements++;
    }
    
    //getMedian
    private int getMedian() {
        return MaxHeap.peek();
    }
}