最近几天详细的阅读了一篇经典的关于软件性能的文章,阅后解答了我很多迷惑,这篇博客就把自己阅读后的一些思考和总结分享一下,如有不能理解或想阅览具体内容的请参考原文和译文内容。。。。
原文地址:Thinking Clearly About Performance
译文下载链接:认清性能问题
1、响应时间VS吞吐量
通常来说,响应时间和吞吐量承反比例(响应时间越长吞吐量越低)。
PS:博客发布后测试群的一个大神说第一点存在描述问题,于是我们就这一点聊了些相关的话题,大概的内容和结论是这样的:
①、响应时间和吞吐量并没有直接的关系(但是有间接关系);
②、性能优化是需要多维度去衡量和优化的领域;
③、一般来说,性能优化的目标是:在尽量保持和降低响应时间的情况下,不断提高吞吐量,提高流量高峰时间的系统服务可用性(大多数情况,而非全部);
④、响应时间、吞吐量、可用性等因素有时候存在矛盾,需要综合考虑业务情况、系统模块的依赖关系、处理方式(单线程/多线程/负载均衡)等因素,做到合理取舍;
2、描述响应时间的方式
尽量用百分比的方式而非平均值来描述响应时间!————用户感知到的是差异变化,而非平均!
3、性能需求指标
性能需求指标应该是明确描述的、可量化的指标需求。
4、性能剖析思路
找到最慢的几个任务(消耗时间最多),分析它们是否有对应关系,每个任务的时间占比,得到一个明确的描述:每个任务运行消耗了多少时间!
5、阿姆达尔定律
系统对某一部件采用更快执行方式所能获得的系统性能提升程度,取决于这种执行方式被使用的频率,或所占总执行时间的比例。
6、性能优化排序
优先占用资源最多或消耗时间最多的任务,但要考虑优化的成本、收益、风险(没有最好的方案,只有最合适的方案)。
7、偏斜度
表示在一组响应时间值中的非一致性程度(比如下面两组值的对比)
①、表现值和实际值
②、平均响应时间和95%响应时间
8、最小化风险
确认问题根节点,不要让局部影响到全局。
9、提升效率
性能优化优先原则:首先专注于业务上最需要优先修正的程序,而不是从全局调优来改善性能。
10、负载
负载的一个直观测量指标:使用率(反映了资源按时间分片的使用情况);
负载会在并发任务执行时引发资源竞争;
引起负载上升系统变慢的2个原因:队列延迟和相关性延迟(资源竞争,等待,死锁等)
11、响应时间
特点:在具备完美扩展性的前提下:RT=servertime(任务执行时间)+querywaittime(队列等待时间)
12、拐点
响应时间和吞吐量之间的某个最优负载平衡点的资源使用率的值,称为拐点。
计算公式:响应时间/资源利用率=所得结果最小的值
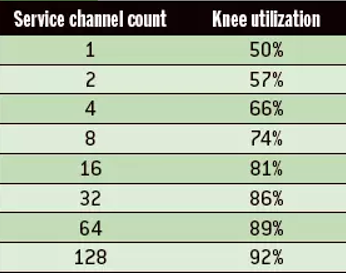
13、拐点相关性
在完美扩展性前提下,只要系统的平均负载超过拐点,那么系统依然会面临性能瓶颈,实际生产中的拐点比上图的拐点数值更小。
拐点主要有以下几个特点:
①、系统中的每一项资源都存在拐点;
②、系统的拐点都≤上图中给出的值,系统的扩展完美型越差,拐点越小;
③、对于请求随机到达的系统,如果资源负载持续超过拐点,那么将遇到性能瓶颈;
14、随机到达
随机任务请求往往会聚集等待并引发短暂的资源使用率上升,需要足够的容量来消费。这种情况下可能会引发队列延迟并导致响应时间的明显波动。(等待时间参考:2/5/8原则)
15、容量规划
容量规划特点:
①、某项资源的容量就是高峰期可以轻松运行任务而资源使用率不会超过拐点的值;
②、保持资源利用率低于拐点,系统表现则基本不会低于我们的期望值;
③、如果系统中某项资源超过它的拐点,就会遇到性能瓶颈;
④、遇到容量瓶颈,解决方式是:重新配置负载分配(减少负载OR增加容量);
关于这篇文章,最后提及到了一个很明确的观点:过早的考虑优化系统性能,是一场灾难!!!