初级模拟电路：10-2 分贝与伯德图

回到目录

      本章的主要内容，就是研究输入信号的频率的变化对放大器增益的影响，在开始正式研究之前，本小节还要介绍两个工具，一个是归一化单位，一个是伯德图。

1. 归一化单位

      通常，输入信号的频率对一个放大电路增益的影响，典型如下图所示：

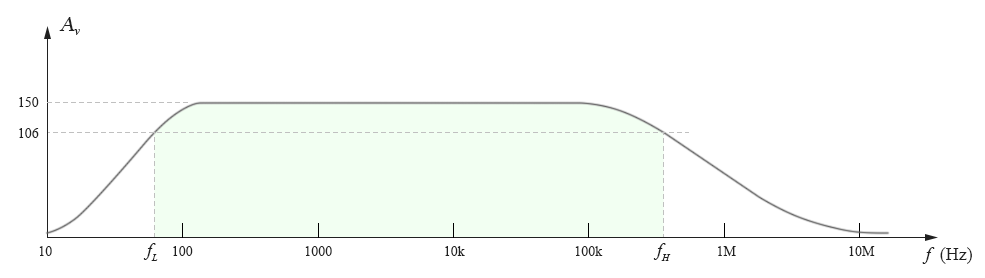
图10-2.01 

      从图中可以看到，这是一个半对数坐标图，其横坐标（频率）为对数坐标，纵坐标（电压增益）为线性坐标。在图中我们可以观察到，在中频范围内（约 100Hz~100kHz），其电压增益可达到最大值（图中为150），在输入信号低于100Hz或高于100kHz时，其电压增益都会减小。

      一般我们会比较关注电压增益减小到其最大增益的0.707（即1/√2）时的左右两个频率点（图中为f_L和f_H），因为从最原始的电路定义来看，当电压值降为0.707倍时，根据电压与功率的换算关系，输出功率会减小到原来的1/2，当输出功率降到原来的一半以下时，通常我们就认为这个电路已经不算正常工作了。

      我们把在这两个频率点之间的频率范围，称为：带宽（bandwidth）。相应的f_L和f_H称为：截止频率（cutoff frequency）或拐点频率（corner frequency）。

      在很多情况下，我们在比较不同的放大电路的性能优劣的时候，仅仅关注它们的频率带宽，而并不太关注其真正的放大倍数（因为放大倍数通常可以通过配置不同的电阻来调节，而带宽通常是由电路的设计结构或器件的性质决定，一般是无法调节的）。因此，人们在纵坐标上使用了归一化（normalized）方法，将纵坐标的值表示为每个频率点的实际增益与最大增益值的比值，这样就完成了归一化，纵坐标的最大值为1，且无量纲，如下图所示：

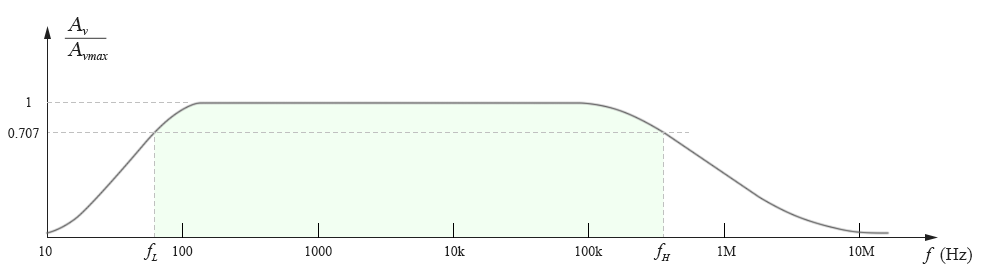
图10-2.02 

      通过归一化以后，我们就可以比较不同放大电路之间的带宽性能了。比如，通过比较下面的两个放大电路的归一化增益-频率图，我们可以明显看出左图放大器的频率性能（带宽）要好于右图：

图10-2.03 

2. 伯德图

      若将纵坐标再作进一步变化，将纵坐标也变为分贝表示，就得到了所谓的伯德图（Bode plot）。上面图10-2.02的归一化图变成伯德图后，如下图所示：

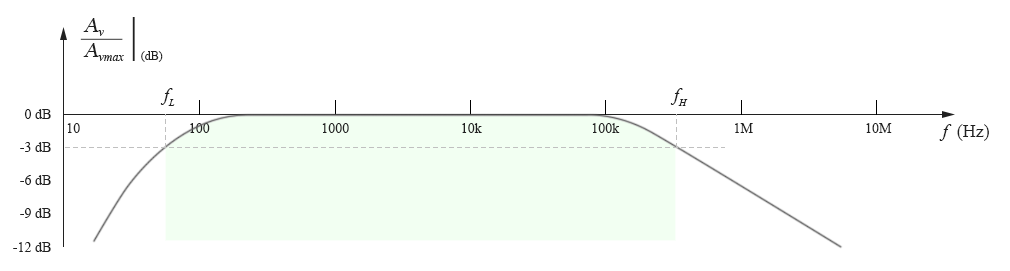
图10-2.04 

      在图中，原来纵坐标为0.707的的值，现在变为了-3dB：

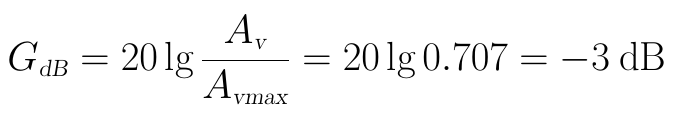
      现在，纵坐标也变成了对数坐标，成为了“全对数坐标图”。根据上一小节对于分贝的广义定义，对于衰减到0.707倍的比值，人们一般直接说成衰减了3dB（或增益为-3dB）,而不再关注这个物理量本身的性质。-3dB是个重要的指标，后面会经常碰到。

      你可能会觉得有些疑惑，归一化单位图用着也蛮好，为什么要再给自己增加麻烦，把纵坐标变为分贝表示呢？其实伯德图的好处，在于它可以把上面看上去非线性的“增益-频率”曲线图，变成线性图。我们将在下一小节实际使用一下伯德图，分析一个最简单的RC电路，你就明白伯德图的好处了。

（1）RC电路基本参数

      下图是一个简单的RC高通滤波电路，虽然不是放大电路，但我们可以将输出电压V_o与输入电压V_i的比值视为电压增益，来分析其电压增益与频率的关系。（以下关于交流电压电流的符号我们都用其相量符号表示）

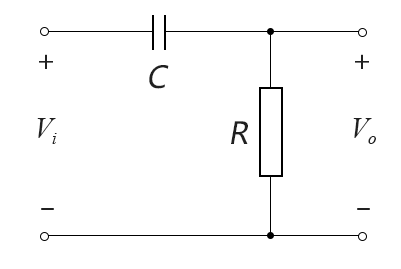
图10-2.05 

      当电路工作在中高频时，电容C可视为短路，输出V_o等于输入V_i，其增益达到最大值，为1，即：

      当电路工作在低频时，电容C会对交流电造成阻碍，使得输出V_o小于输入V_i，根据电路原理中关于电容器的基本知识，其容抗的表达式为：

      （注意：虽然容抗X_C的单位也是欧姆，但其在相量数值上是个虚数。）

      输出电压V_o的表达式为：

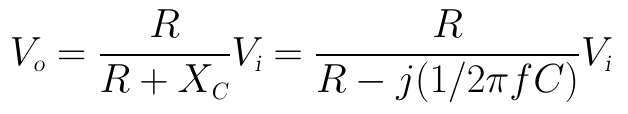
      因此输出电压的幅值表达式为：

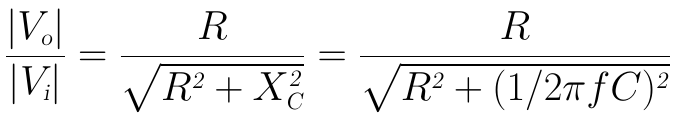
      其实际增益A_v为输出电压与输入电压幅值的比值，即：

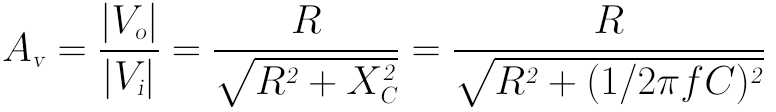
      从上式可以看出，当频率f趋于0时，X_C趋于无穷大，实际增益趋于0；当频率f趋于无穷大时，X_C趋于0，实际增益趋于1。

      现在再来计算截止频率f_L：我们希望频率为f_L时，实际增益A_v与理论上最大增益A_vmax的比值为0.707：

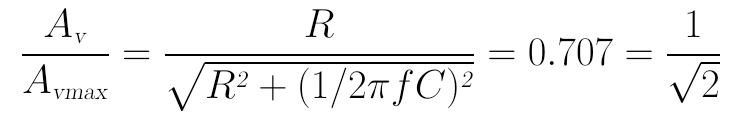
      上式可解得，当f为：

      时，电压幅值的归一化增益为0.707。电压幅值增益-频率图大致如下图所示：

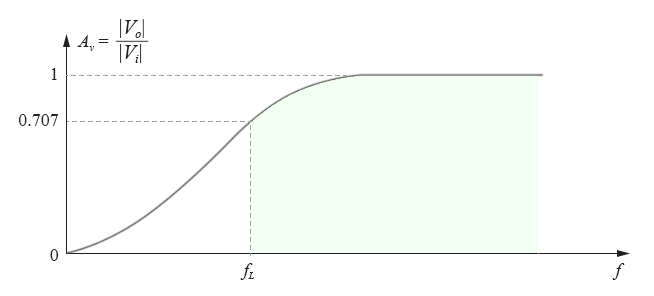
图10-2.06 

（2）使用伯德图

      好，现在来看如何利用伯德图将上面的频率图线性化。前面我们已经得到电压幅值的归一化增益的表达式为：

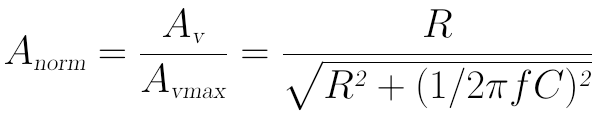
      将前面算得的f_L稍微变化一下可得：

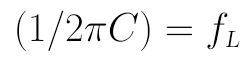
      将这个 (1/2πC) 代入上式的归一化增益，可得：

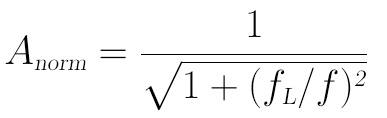
      现在将这个电压幅值的归一化增益使用分贝表示，计算过程为：

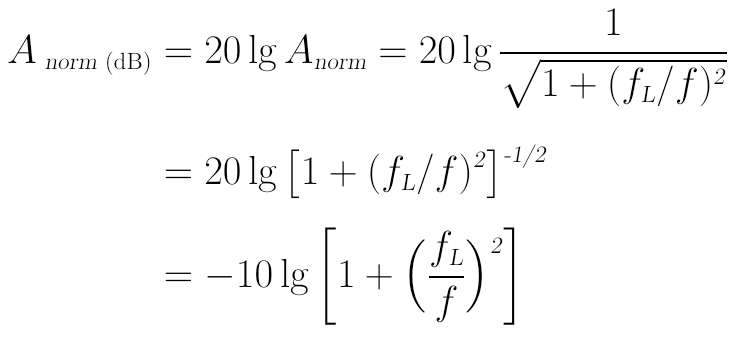
      当f远大于截止频率f_L时，上式中的(f_L/f)2项值会远小于1，因此可被近似掉；而当f远小于f_L时，上式中的1可被近似掉；而因此电压幅值的增益可写成分段函数：

      上面的分段函数若画在伯德图上，第一个式子的0dB就是一条与x轴重合的水平直线，比较简单。关键是第2个式子，还要再化简一番才能看出其线性：

      上式中，前项-20lg(f_L) 是一个常数，而后项在对数横坐标的情况下，lg(f)可视为一个整体，即为x轴因子，因此上式在对数坐标图上的纯表达式可看作：

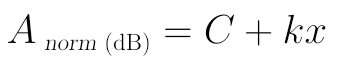
      这个就是一个线性表达式了，只不过仅在“分贝-对数图”上呈线性而已，如是将上面的分段函数画在伯德图上就如下图所示：

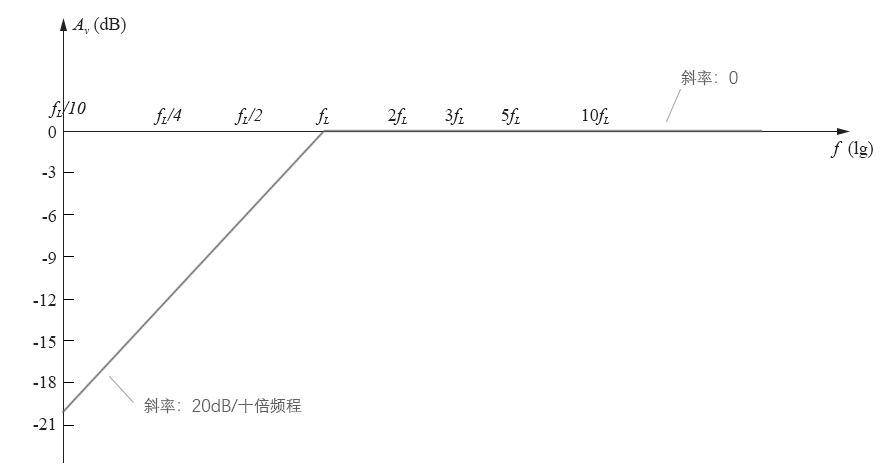
图10-2.07 

      其频率f小于f_L时，电压幅值归一化增益 Anorm近似为一条斜率k等于20、且通过横坐标上f_L点的直线；当频率f大于f_L时，。电压幅值归一化增益 Anorm近似为一条与x轴重合的水平直线。

      根据我们前面小节关于“十倍程”用法的解释，这条斜率为20的直线可以称为：20dB/十倍频程。在实际使用中，有时人们会嫌20这个系数太大了，写起来不方便；对于同样的斜率，有时会用一个更小的单位：/倍频程（即：频率增加1倍时，纵坐标的分贝变化数量）。“20dB/十倍频程”约等同于“6dB/倍频程”。换算方法如下：

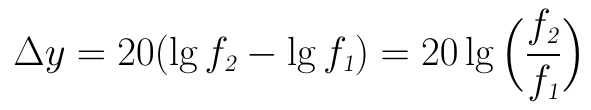
      当f2/f1=2时：

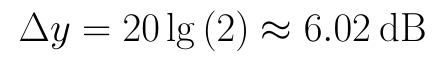
      最后的问题是，这样线性化以后，在f≫f_L和f≪f_L的情况下近似性是比较好的，但在f靠近f_L的地方不太准，需要手工修正。于是我们再算几个f比较靠近f_L时的值：

      然后将它们拟合到伯德图上，于是真正的电压幅值增益曲线就如下图中的绿色曲线所示：

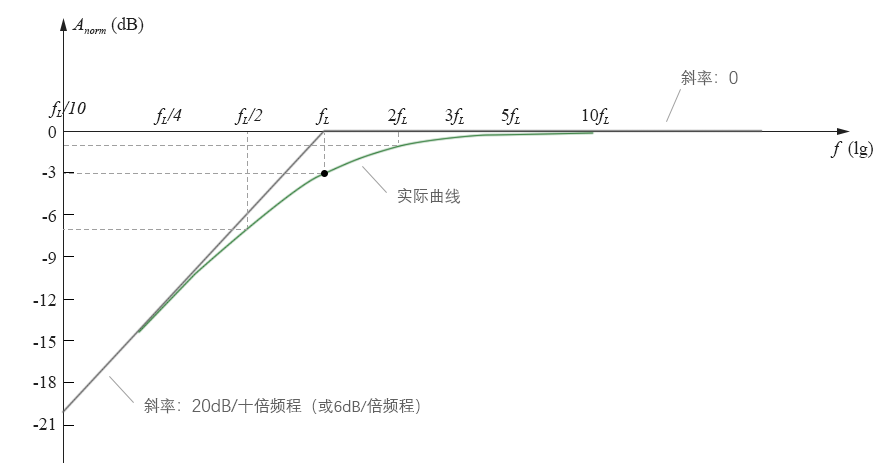
图10-2.08 

      在理解了伯德图是如何将曲线线性化后，我们以后在使用伯德图时可以不仅仅局限于归一化单位，只要纵坐标为任何比值（比如V_o/V_i），都可以将其在伯德图上进行表示。

      最后值得一提的是，这种线性近似化方法在以前没有计算机的那个时代是很有用的（伯德最初是在1945年发表了这个伯德图方法），它可以帮助人们大大减少计算量，方便对电路或系统进行分析。这种方法即便在今天也不算过时，需要很好地掌握，因为使用它可以迅速地把握住系统的主要特征。

      不过，在如今这个计算机已经普及的时代，绘制精确的增益图或响应图也不是什么难事了，比如使用Python的SciPy和Matplotlib库，可以快速地绘制出精准的伯德图和其他各种曲线，而且这么好的软件居然还是免费的。推荐学习一下，不负这个时代的好时光。

（3）相位分析

      伯德图一般只能将增益幅值线性化，对于相位响应没法线性化，只能老老实实算出若干个典型值，然后在图上将这些点拟合成一条曲线。我们这里就演示一下如何绘制上面的RC电路的相位响应对数图。

      重写上面的电压增益的原始表达式如下：

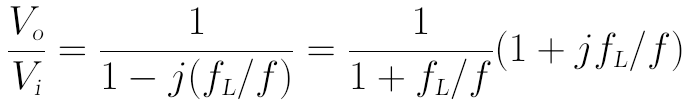
      其相位响应θ的表达式为：

      当f≪f_L时：

      当f≫f_L时：

      再计算几个典型频率时的值：

      根据这几个点位的相位值，我们可以拟合出一条大致的相位响应曲线，如下图所示：

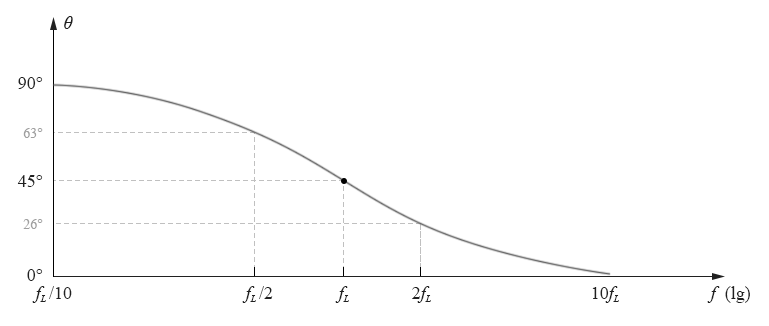
图10-2.09 

     

回到目录

欢迎关注本博公众号，可方便在手机端访问和索引本博技术文章：

（ end of 10-2）

---