Poj 2891中国剩余定理,非互素
x=a1(mod n1)
x=a2(mod n2)
n1与n2不互素。
x=n1k1+a1
x=n2k2+a2
n1k1=n2k2+a2-a1
n1k1=a2-a1(mod n2)
若k1有解,则gcd(n1,n2)|(a2-a1)
设d=gcd(n2,n1)
即 n1k1/d=(a2-a1)/d(mod n2/d)
k1=(a2-a1)/d*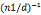 (mod n2/d)
(mod n2/d)
设k1=(a2-a1)/d*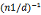 +k(n2/d)
+k(n2/d)
所以x=n1k1+a1=n1((a2-a1)/d*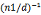 )+k(n2/d))+a1
)+k(n2/d))+a1
x=n1*(a2-a1)*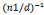 /d+a1(mod n1n2/d)
/d+a1(mod n1n2/d)
令t=(a2-a1)*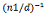 ,n=n1n2/d
,n=n1n2/d
x=tn1+a2(mod n)
故,将所有的方程可合并成一个
代码:
#include <iostream>
#include <stdio.h>
using namespace std;
typedef long long ll;
ll b[10000],w[10000];//a=b[i](%w[i]);
ll mod;
ll gcd(ll a,ll b)
{
if(b==0)
return a;
else
return gcd(b,a%b);
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{
if(0==b){x=1;y=0;return a;}
ll d=exgcd(b,a%b,x,y);
ll t=x;x=y;y=t-a/b*y;
return d;
}
ll invmod(ll a,ll n)//求a对n的乘法逆元
{
ll x,y;
if(exgcd(a,n,x,y)!=1) return -1;
return (x%n+n)%n;
}
bool merge(ll a1,ll n1,ll a2,ll n2,ll &a3,ll &n3)
{
ll d=gcd(n1,n2);
ll c=a2-a1;
if(c%d)//若不能整除,则无解
return 0;
c=(c%n2+n2)%n2;
c/=d;
n1/=d;
n2/=d;
c*=invmod(n1,n2);
c%=n2;
c*=n1*d;
c+=a1;
n3=n1*n2*d;
a3=(c%n3+n3)%n3;
return 1;
}
ll china2(ll b[],ll w[],ll k)//a=b[i](%w[i]);
{
ll b1=b[0],w1=w[0],b2,w2,bb,ww,i;
for(i=0;i<k;i++)
{
b2=b[i];
w2=w[i];
if(!merge(b1,w1,b2,w2,bb,ww))
return -1;
b1=bb;
w1=ww;
}
mod=w1;//最后的除数
return (b1%w1+w1)%w1;
}
int main()
{
ll k,i;
freopen("in.txt","r",stdin);
while(scanf("%lld",&k)!=EOF)
{
for(i=0;i<k;i++)
scanf("%lld%lld",w+i,b+i);
printf("%lld\n",china2(b,w,k));
}
return 0;
}