算法导论数论一般离散对数问题

一般离散对数问题（GDLP）（摘自天津大学PPT）

1.一般离散对数问题（GDLP）：给定一个n阶的有限循环群G和它的一个原根，以及元素b，求一个整数x（0≤x≤n-1），使得a^x=b(modn)

 

2.Baby-step Giant-step，令m=(p-1)^1/2，如果b=a^x，那么可以把x重写为x=i*m+j，其中0 ≤ i, j < m，于是b=a^i*m * a^j，两边同除得b(a^-m)ⁱ=a^j，然后可以通过下面的算法来计算x

3.例：令p=113，a=3，b=57执行算法：

m=11

计算出的二元组排好序为：

j 0 1 8 2 5 9 3 7 6 10 4

3^j(mod 113) 1 3 7 9 17 21 27 40 51 63 81

计算a^-1=3^-1(mod 113) = 38，然后计算a^-m=38¹¹(mod 113) = 58

执行循环过程中r=b*a^-mi，查找过程中的(i, r)为：

i 0 1 2 3 4 5 6 7 8 9

r 57 29 100 37 112 55 26 39 2 3

最终返回：i * m + j = 9 * 11 + 1 = 100

4.判断a是否是Z_n^*的原根：

定理：设n>1，φ(n)的所有不同素因数是p1, p2, …, pk。gcd(a, n) = 1，则a是Z_n^*的原根的充要条件是：

对于所有的i(1≤i≤k)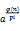，(modn)!=1；