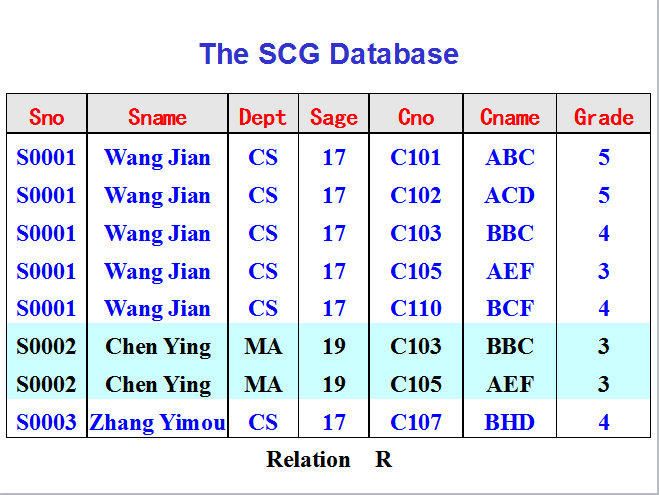


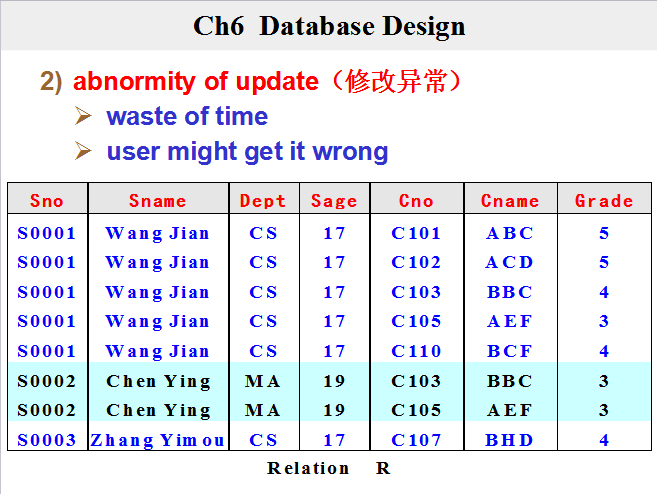
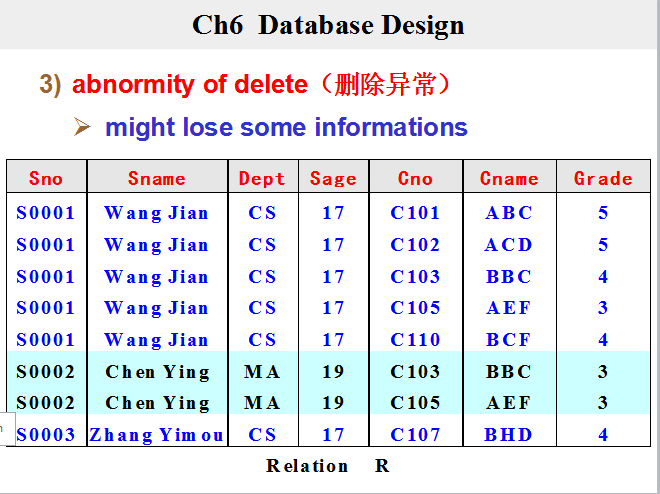

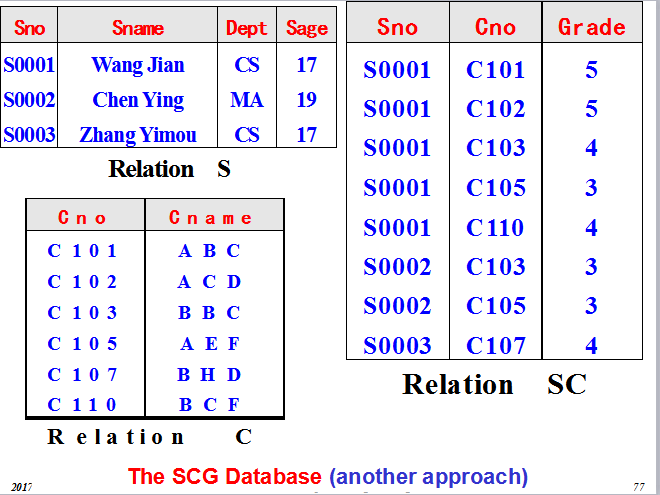



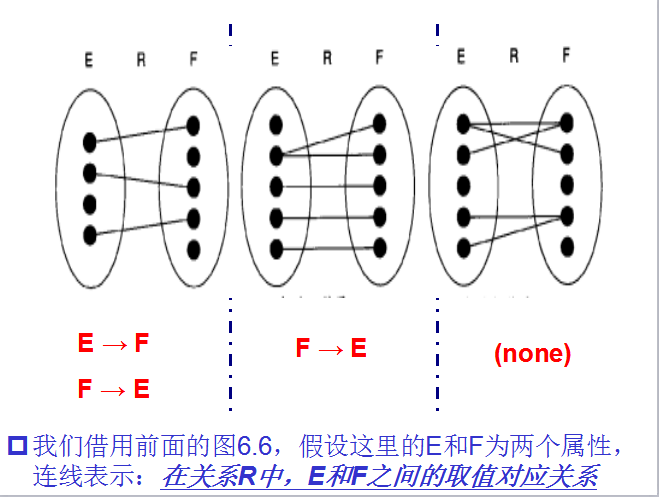
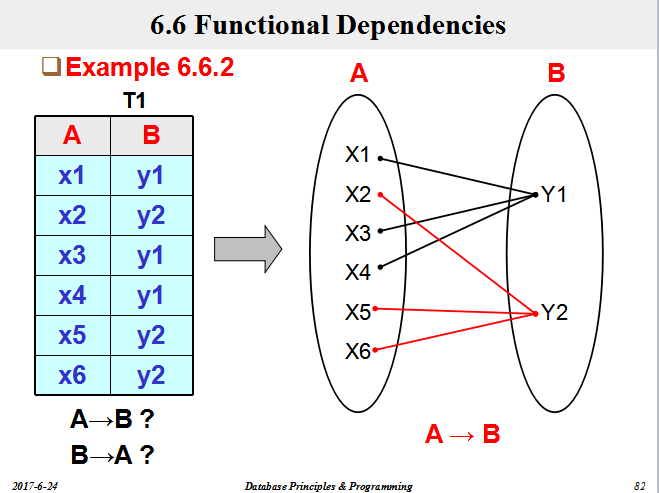
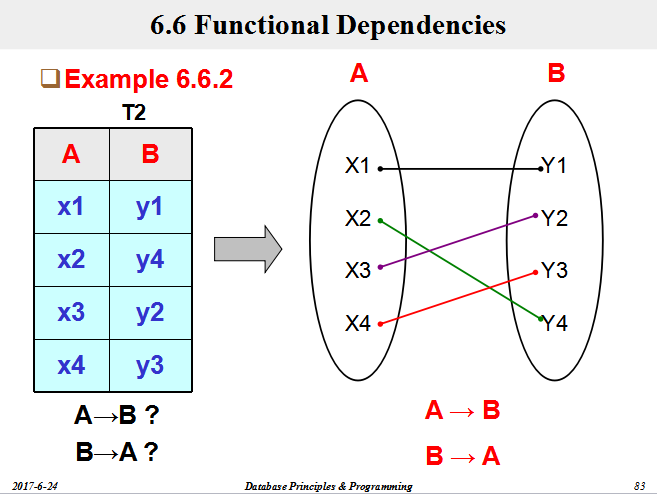



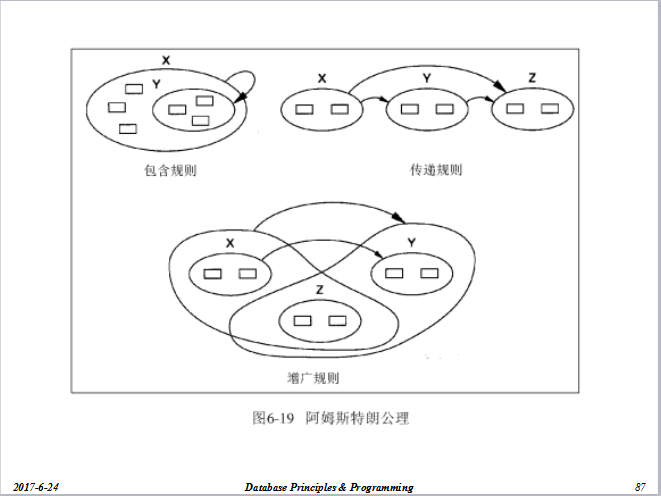























一、等价和覆盖
定义:关系模式R<u,f>上的两个依赖集F和G,如果F+=G+,则称F和G是等价的,记做F≡G。若F≡G,则称G是F的一个覆盖,反之亦然。两个等价的函数依赖集在表达能力上是完全相同的。
二、最小函数依赖集
定义:如果函数依赖集F满足下列条件,则称F为最小函数依赖集或最小覆盖。
① F中的任何一个函数依赖的右部仅含有一个属性;
② F中不存在这样一个函数依赖X→A,使得F与F-{X→A}等价;
③ F中不存在这样一个函数依赖X→A,X有真子集Z使得F-{X→A}∪{Z→A}与F等价。
算法:计算最小函数依赖集。
输入 一个函数依赖集
输出 F的一个等价的最小函数依赖集G
步骤:① 用分解的法则,使F中的任何一个函数依赖的右部仅含有一个属性;
② 去掉多余的函数依赖:从第一个函数依赖X→Y开始将其从F中去掉,然后在剩下的函数依赖中求X的闭包X+,看X+是否包含Y,若是,则去掉X→Y;否则不能去掉,依次做下去。直到找不到冗余的函数依赖;
③去掉各依赖左部多余的属性。一个一个地检查函数依赖左部非单个属性的依赖。例如XY→A,若要判Y为多余的,则以X→A代替XY→A是否等价?若A
(X)+,则Y是多余属性,可以去掉。
举例:已知关系模式R<u,f>,U={A,B,C,D,E,G},F={AB→C,D→EG,C→A,BE→C,BC→D,CG→BD,ACD→B,CE→AG},求F的最小函数依赖集。
解1:利用算法求解,使得其满足三个条件
① 利用分解规则,将所有的函数依赖变成右边都是单个属性的函数依赖,得F为:F={AB→C,D→E,D→G,C→A,BE→C,BC→D,CG→B,CG→D,ACD→B,CE→A,CE→G}
② 去掉F中多余的函数依赖
A.设AB→C为冗余的函数依赖,则去掉AB→C,得:F1={D→E,D→G,C→A,BE→C,BC→D,CG→B,CG→D,ACD→B,CE→A,CE→G}
计算(AB)F1+:设X(0)=AB
计算X(1):扫描F1中各个函数依赖,找到左部为AB或AB子集的函数依赖,因为找不到这样的函数依赖。故有X(1)=X(0)=AB,算法终止。
(AB)F1+= AB不包含C,故AB→C不是冗余的函数依赖,不能从F1中去掉。
B.设CG→B为冗余的函数依赖,则去掉CG→B,得:F2={AB→C,D→E,D→G,C→A,BE→C,BC→D,CG→D,ACD→B,CE→A,CE→G}
计算(CG)F2+:设X(0)=CG
计算X(1):扫描F2中的各个函数依赖,找到左部为CG或CG子集的函数依赖,得到一个C→A函数依赖。故有X(1)=X(0)∪A=CGA=ACG。
计算X(2):扫描F2中的各个函数依赖,找到左部为ACG或ACG子集的函数依赖,得到一个CG→D函数依赖。故有X(2)=X(1)∪D=ACDG。
计算X(3):扫描F2中的各个函数依赖,找到左部为ACDG或ACDG子集的函数依赖,得到两个ACD→B和D→E函数依赖。故有X(3)=X(2)∪BE=ABCDEG,因为X(3)=U,算法终止。
(CG)F2+=ABCDEG包含B,故CG→B是冗余的函数依赖,从F2中去掉。
C.设CG→D为冗余的函数依赖,则去掉CG→D,得:F3={AB→C,D→E,D→G,C→A,BE→C,BC→D,ACD→B,CE→A,CE→G}
计算(CG)F3+:设X(0)=CG
计算X(1):扫描F3中的各个函数依赖,找到左部为CG或CG子集的函数依赖,得到一个C→A函数依赖。故有X(1)=X(0)∪A=CGA=ACG。
计算X(2):扫描F3中的各个函数依赖,找到左部为ACG或ACG子集的函数依赖,因为找不到这样的函数依赖。故有X(2)=X(1),算法终止。(CG)F3+=ACG。
(CG)F3+=ACG不包含D,故CG→D不是冗余的函数依赖,不能从F3中去掉。
D.设CE→A为冗余的函数依赖,则去掉CE→A,得:F4={AB→C,D→E,D→G,C→A,BE→C,BC→D,CG→D,ACD→B,CE→G}
计算(CG)F4+:设X(0)=CE
计算X(1):扫描F4中的各个函数依赖,找到左部为CE或CE子集的函数依赖,得到一个C→A函数依赖。故有X(1)=X(0)∪A=CEA=ACE。
计算X(2):扫描F4中的各个函数依赖,找到左部为ACE或ACE子集的函数依赖,得到一个CE→G函数依赖。故有X(2)=X(1)∪G=ACEG。
计算X(3):扫描F4中的各个函数依赖,找到左部为ACEG或ACEG子集的函数依赖,得到一个CG→D函数依赖。故有X(3)=X(2)∪D=ACDEG。
计算X(4):扫描F4中的各个函数依赖,找到左部为ACDEG或ACDEG子集的函数依赖,得到一个ACD→B函数依赖。故有X(4)=X(3)∪B=ABCDEG。因为X(4)=U,算法终止。
(CE)F4+=ABCDEG包含A,故CE→A是冗余的函数依赖,从F4中去掉。
③ 去掉F4中各函数依赖左边多余的属性(只检查左部不是单个属性的函数依赖)由于C→A,函数依赖ACD→B中的属性A是多余的,去掉A得CD→B。
故最小函数依赖集为:F={AB→C,D→E,D→G,C→A,BE→C,BC→D,CG→D,CD→B,CE→G}
解2:利用Armstrong公理系统的推理规则求解
① 假设CG→B为冗余的函数依赖,那么,从F中去掉它后能根据Armstrong公理系统的推理规则导出。
因为CG→D (已知)
所以CGA→AD,CGA→ACD (增广律)
因为ACD→B (已知)
所以CGA→B (传递律)
因为C→A (已知)
所以CG→B (伪传递律)
故CG→B是冗余的。
② 同理可证:CE→A是多余的。
③ 又因C→A,可知函数依赖ACD→B中的属性A是多余的,去掉A得CD→B。
故最小函数依赖集为:F={AB→C,D→E,D→G,C→A,BE→C,BC→D,CG→D,CD→B,CE→G}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
//数据库编程实验//求最小覆盖Fm //输入:属性全集U,U上的函数依赖集F//输出:函数依赖集F的最小覆盖Fm #include <iostream>#include <string>using namespace std;struct FunctionDependence//函数依赖 { string X;//决定因素 string Y; };void Init (FunctionDependence FD[],int n){ //函数依赖关系初始化 int i; string x,y; cout<<"请输入F中的函数依赖(决定因素在左,被决定因素在右)"<<endl; cin="" f="" for="" i="0;i<n;i++)">>x>>y; FD[i].X=x; FD[i].Y=y; } cout<<"函数依赖集合"; cout<<"F={" ; for (i=0;i<n;i++) -="" bool="" count="=length1)" f="" flag="false;" for="" i="0;i<length1;i++)" if="" ii="0;ii<200;ii++)" int="" kk="0;kk<size;kk++)" length1="=length2)" length2="b.length();" return="" size="mm.length();" ss="�" string="">=1) ss+=(char)ii; } return ss;} bool IsIn(string f,string zz)//能够判断F中决定因素f里所有的因素是否在X中,但这样可能导致结果出现重复 { bool flag1=false; int len1=f.length(); int len2=zz.length(); int k=0,t=0,count1=0; for (k=0;k<len1;k++) count1="=len1)" else="" flag1="true;break;" for="" functiondependence="" i="0;i<n;i++)" if="" int="" left-="" return="" string="" t="0;t<len2;t++)">rightvoid Cut(FunctionDependence FD[],int n,string left,string right,FunctionDependence Dyna[]){ int i=0,j=0,count=0; for (i=0;i<n;i++) -="" .x="FD[i].X;" .y="FD[i].Y;" else="" f="{"" j="0;j<count;j++)">"<<dyna[j].y; -="" .x="Dyna1[k].X;" .y="Dyna1[k].Y;" a.y="=b.Y))"" bool="" else="" f="{";" for="" functiondependence="" i="0;i<count1;i++)" if="" int="" j="0;j<count;j++)" k="0;k<count;k++)" return="" void="" y="">"<<dyna3[i].y; -="" .x="FD[i].X;" .y="(FD[i].Y)[j];" count="0;" d="n;" f="{"" fm="<<" for="" functiondependence="" i="0;i<n;i++)" if="" int="" j="0;j<lengthR;j++)//将右部分解成单一属性,添加到属性集合的后面" k="0;k<count;k++)" lengthr="0,i=0,j=0,k=0;" static="" void="">"<<dynamicfd[k].y; cin="" d="count;" functiondependence="" if="" int="" void="">>N; FunctionDependence fd[N]; Fmin(fd,N);// SingleR(fd,N);// CutSameFD(fd,N);// FD(fd,N); return 0;} </dynamicfd[k].y;></dyna3[i].y;></dyna[j].y;></n;i++)></len1;k++)></n;i++)></endl;></string></iostream> |

很后悔没有用链式结构,导致增加删除节点很麻烦,权当作为概念理解的帮助吧。