Topological Sorting

Topological sorting/ ordering is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. We can conduct topological sorting only on DAG (directed acyclic graph). Therefore, topological sorting is often used in scheduling a sequence of jobs or tasks based on their dependencies. Another typical usage is to check whether a graph has circle.

Here is a more detailed description -> Wiki Topological sorting

Below are several algorithms to implement topological sorting. Mostly, the time complexity is O(|V| + |E|).

Algorithm 1 -- Ordinary Way

Time complexity O(|V|^2 + |E|) In Step 1, time complexity O(|V|) for each vertex.

1. Identify vertices that have no incoming edge (If no such edges, graph has cycles (cyclic graph))
2. Select one such vertex
3. Delete this vertex of in-degree 0 and all its outgoing edges from the graph. Place it in the output.
4. Repeat Steps 1 to Step 3 until graph is empty

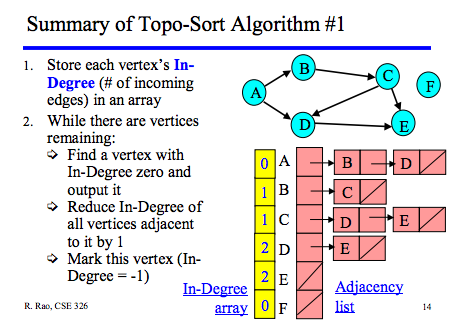
(referrence: cs.washington Topological Sorting)

Algorithm 2 -- Queue

Improve algorithm 1 by use queue to store vertex whose in-degree is 0. Time complex O(|V| + |E|).

Algorithm 3 -- DFS

When we conduct DFS on graph, we find that if we order vertices according to its complete time, the result if one topological sorting solution.

Time complexity O(|V| + |E|)

import java.util.*;

public class TopologicalSort {

  // When we use iteration to implement DFS, we only need 2 status for each vertex
  static void dfs(List<Integer>[] graph, boolean[] used, List<Integer> res, int u) {
    used[u] = true;
    for (int v : graph[u])
      if (!used[v])
        dfs(graph, used, res, v);
    res.add(u);
  }

  public static List<Integer> topologicalSort(List<Integer>[] graph) {
    int n = graph.length;
    boolean[] used = new boolean[n];
    List<Integer> res = new ArrayList<>();
    for (int i = 0; i < n; i++)
      if (!used[i])
        dfs(graph, used, res, i);
    Collections.reverse(res);
    return res;
  }
}

(referrence: DFS: Topological sorting)