洛谷模拟NOIP考试反思

洛谷模拟NOIP考试反思

想法

考了这么简单的试qwq然而依然emmmmmm成绩不好
虽然本次难度应该是大于正常PJ难度的但还是很不理想，离预估分数差很多qwq
于是就有了本反思嘤嘤嘤

比赛链接

原比赛链接（已结束但仍然可提交）

题目解析反思

第一题

超简单（虽然仍然没做对）

第二题

代码扔上来qwq（虽然还是不会）

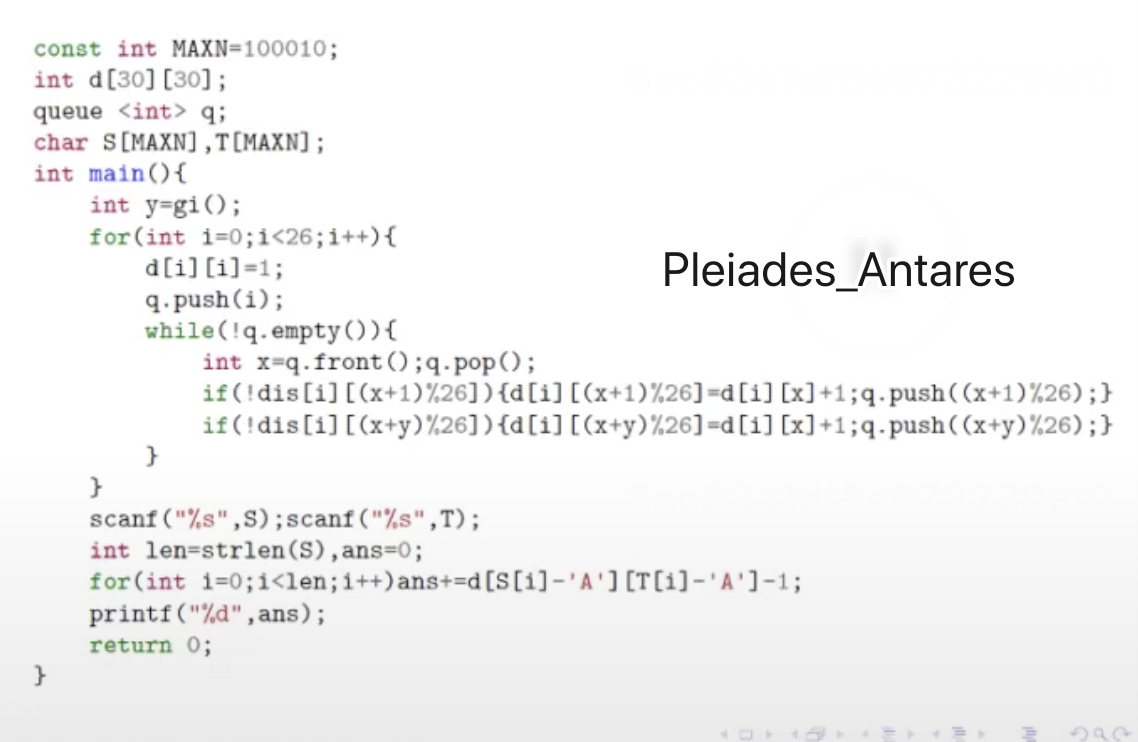
第三题

代码

第四题

毒瘤极了wodema
据说原来数据是50%那里的，但是出题人z某灵机一动加到了1000orz
于是很多人自然而然地想到了状压DP
普及组是到不了这个难度的，主要是z某他太坏了
50分做法（状压）

正解的100分正法并非毒瘤状压qwq

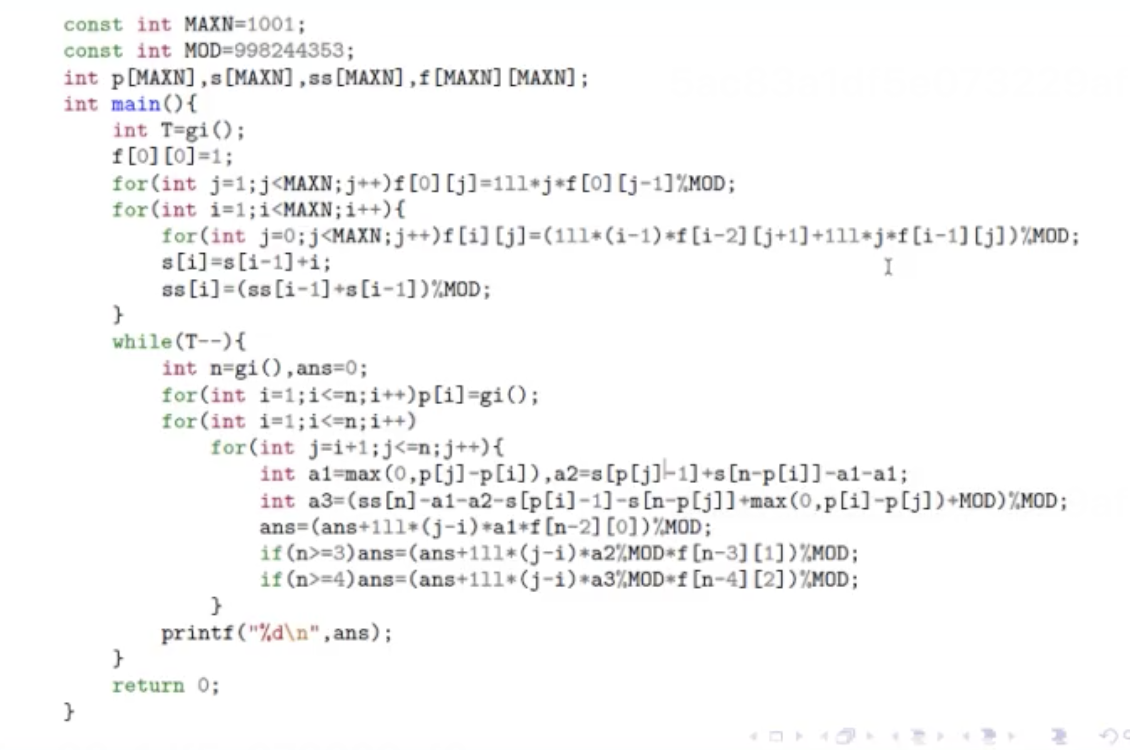
（有人说爆搜能骗40分？！）

讲评者

XD

TG

还是放一道TG第三题压压惊好了

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
typedef long long int LL;
const int Max_N(100050);
const int Max_M(100050);
const int Max_Q(100050);

template<typename Type>
void gi(Type &Ret)
{
    Ret = 0;
    char ch;
    while (ch = getchar(), ch > '9' || ch < '0')
        ;
    do
    {
        (Ret *= 10) += ch - '0';
    }
    while (ch = getchar(), ch >= '0' && ch <= '9');
}

inline int Abs(const int &x)
{
    return x >= 0 ? x : -x;
}

int N, M, Q, X1[Max_N + Max_Q], Y1[Max_N + Max_Q], X2[Max_N + Max_Q], Y2[Max_N + Max_Q];
int L[Max_N + Max_Q], R[Max_N + Max_Q], D[Max_N + Max_Q], U[Max_N + Max_Q], Anc[60][Max_N];
LL T[Max_N + Max_Q], Sum[60][Max_N];

#define LEFT  (segt[cur].l)
#define RIGHT (segt[cur].r)
#define MID   (segt[cur].mid)
#define COV   (segt[cur].Cov)
#define TAG   (segt[cur].Tag)
#define LCH   (cur << 1)
#define RCH   ((cur << 1) | 1)

struct node
{
    int l, r, mid, Cov, Tag;
};
node segt[Max_M << 2];
int C[Max_M];

void build_tree(const int &cur, const int &l, const int &r)
{
    LEFT = l, RIGHT = r, MID = l + ((r - l) >> 1), COV = TAG = 0;
    if (l == r)
        return;
    build_tree(LCH, l, MID), build_tree(RCH, MID + 1, r);
}

inline void cover(const int &cur, const int &v)
{
    COV = TAG = v;
}

inline void pushdown(const int &cur)
{
    if (TAG)
        cover(LCH, TAG), cover(RCH, TAG), TAG = 0;
}

void cover(const int &cur, const int &l, const int &r, const int &v)
{
    if (LEFT == l && RIGHT == r)
    {
        cover(cur, v);
        return;
    }
    pushdown(cur);
    if (r <= MID)
        cover(LCH, l, r, v);
    else
        if (l > MID)
            cover(RCH, l, r, v);
        else
            cover(LCH, l, MID, v), cover(RCH, MID + 1, r, v);
}

int query(const int &cur, const int &pos)
{
    if (LEFT == RIGHT)
        return COV;
    pushdown(cur);
    if (pos <= MID)
        return query(LCH, pos);
    else
        return query(RCH, pos);
}

inline bool compL(const int &a, const int &b)
{
    return min(X1[a], X2[a]) < min(X1[b], X2[b]);
}

void goL()
{
    build_tree(1, 0, M), memset(C, 0, sizeof(C));
    sort(L + 1, L + 1 + L[0], compL);
    sort(R + 1, R + 1 + R[0], compL);
    sort(D + 1, D + 1 + D[0], compL);
    sort(U + 1, U + 1 + U[0], compL);
    for (int l = 1, r = 1, d = 1, u = 1, a, b, p;l <= L[0];++l)
    {
        p = L[l];
        while (r <= R[0] && X1[R[r]] <= X2[p])
        {
            if (R[r] <= N)
                C[Y2[R[r]]] = R[r];
            ++r;
        }
        while ((d <= D[0] && X2[D[d]] <= X2[p]) || (u <= U[0] && X2[U[u]] <= X2[p]))
            if ((d <= D[0]) && (u > U[0] || X2[D[d]] <= X2[U[u]]))
            {
                if (D[d] <= N)
                    cover(1, Y2[D[d]], Y1[D[d]], D[d]);
                ++d;
            }
            else
            {
                if (U[u] <= N)
                    cover(1, Y1[U[u]], Y2[U[u]], U[u]);
                ++u;
            }
        a = query(1, Y2[p]), b = C[Y2[p]];
        if (p <= N)
        {
            if (a == 0 && b == 0)
                Anc[0][p] = -1;
            else
                if (a && (b == 0 || X2[p] - X2[a] < X2[p] - X2[b]))
                    Anc[0][p] = a, Sum[0][p] = (X2[p] - X2[a]) + Abs(Y2[p] - Y2[a]);
                else
                    Anc[0][p] = b, Sum[0][p] = X2[p] - X2[b];
        }
        else
        {
            if (a == 0 && b == 0)
                X2[p] = max(0LL, X2[p] - T[p]), T[p] = 0LL;
            else
                if (a && (b == 0 || X2[p] - X2[a] < X2[p] - X2[b]))
                    if (T[p] <= X2[p] - X2[a])
                        X2[p] -= T[p], T[p] = 0LL;
                    else
                    {
                        T[p] -= X2[p] - X2[a], X2[p] = X2[a];
                        if (T[p] <= Abs(Y2[p] - Y2[a]))
                        {
                            if (Y2[a] <= Y2[p])
                                Y2[p] -= T[p];
                            else
                                Y2[p] += T[p];
                            T[p] = 0LL;
                        }
                        else
                            T[p] -= Abs(Y2[p] - Y2[a]), X2[p] = a;
                    }
                else
                    if (T[p] <= Abs(X2[p] - X2[b]))
                    {
                        if (X2[b] <= X2[p])
                            X2[p] -= T[p];
                        else
                            X2[p] += T[p];
                        T[p] = 0LL;
                    }
                    else
                        T[p] -= Abs(X2[p] - X2[b]), X2[p] = b;
        }
    }
}

inline int getR(const int &x)
{
    return max(X1[x], X2[x]);
}

inline bool compR(const int &a, const int &b)
{
    return getR(a) > getR(b);
}

void goR()
{
    build_tree(1, 0, M), memset(C, 0, sizeof(C));
    sort(L + 1, L + 1 + L[0], compR);
    sort(R + 1, R + 1 + R[0], compR);
    sort(D + 1, D + 1 + D[0], compR);
    sort(U + 1, U + 1 + U[0], compR);
    for (int l = 1, r = 1, d = 1, u = 1, a, b, p;r <= R[0];++r)
    {
        p = R[r];
        while (l <= L[0] && getR(L[l]) >= getR(p))
        {
            if (L[l] <= N)
                C[Y2[L[l]]] = L[l];
            ++l;
        }
        while ((d <= D[0] && getR(D[d]) >= getR(p)) || (u <= U[0] && getR(U[u]) >= getR(p)))
            if ((d <= D[0]) && (u > U[0] || getR(D[d]) >= getR(U[u])))
            {
                if (D[d] <= N)
                    cover(1, Y2[D[d]], Y1[D[d]], D[d]);
                ++d;
            }
            else
            {
                if (U[u] <= N)
                    cover(1, Y1[U[u]], Y2[U[u]], U[u]);
                ++u;
            }
        a = query(1, Y2[p]), b = C[Y2[p]];
        if (p <= N)
        {
            if (a == 0 && b == 0)
                Anc[0][p] = -1;
            else
                if (a && (b == 0 || X2[a] - X2[p] < X2[b] - X2[p]))
                    Anc[0][p] = a, Sum[0][p] = (X2[a] - X2[p]) + Abs(Y2[p] - Y2[a]);
                else
                    Anc[0][p] = b, Sum[0][p] = X2[b] - X2[p];
        }
        else
        {
            if (a == 0 && b == 0)
                X2[p] = min(M * 1LL, X2[p] + T[p]), T[p] = 0LL;
            else
                if (a && (b == 0 || X2[a] - X2[p] < X2[b] - X2[p]))
                    if (T[p] <= X2[a] - X2[p])
                        X2[p] += T[p], T[p] = 0LL;
                    else
                    {
                        T[p] -= X2[a] - X2[p], X2[p] = X2[a];
                        if (T[p] <= Abs(Y2[p] - Y2[a]))
                        {
                            if (Y2[a] <= Y2[p])
                                Y2[p] -= T[p];
                            else
                                Y2[p] += T[p];
                            T[p] = 0LL;
                        }
                        else
                            T[p] -= Abs(Y2[p] - Y2[a]), X2[p] = a;
                    }
                else
                    if (T[p] <= Abs(X2[b] - X2[p]))
                    {
                        if (X2[b] <= X2[p])
                            X2[p] -= T[p];
                        else
                            X2[p] += T[p];
                        T[p] = 0LL;
                    }
                    else
                        T[p] -= Abs(X2[b] - X2[p]), X2[p] = b;
        }
    }
}

inline int getD(const int &x)
{
    return min(Y1[x], Y2[x]);
}

inline bool compD(const int &a, const int &b)
{
    return getD(a) < getD(b);
}

void goD()
{
    build_tree(1, 0, M), memset(C, 0, sizeof(C));
    sort(L + 1, L + 1 + L[0], compD);
    sort(R + 1, R + 1 + R[0], compD);
    sort(D + 1, D + 1 + D[0], compD);
    sort(U + 1, U + 1 + U[0], compD);
    for (int l = 1, r = 1, d = 1, u = 1, a, b, p;d <= D[0];++d)
    {
        p = D[d];
        while (u <= U[0] && getD(U[u]) <= getD(p))
        {
            if (U[u] <= N)
                C[X2[U[u]]] = U[u];
            ++u;
        }
        while ((l <= L[0] && getD(L[l]) <= getD(p)) || (r <= R[0] && getD(R[r]) <= getD(p)))
            if ((l <= L[0]) && (r > R[0] || getD(L[l]) <= getD(R[r])))
            {
                if (L[l] <= N)
                    cover(1, X2[L[l]], X1[L[l]], L[l]);
                ++l;
            }
            else
            {
                if (R[r] <= N)
                    cover(1, X1[R[r]], X2[R[r]], R[r]);
                ++r;
            }
        a = query(1, X2[p]), b = C[X2[p]];
        if (p <= N)
        {
            if (a == 0 && b == 0)
                Anc[0][p] = -1;
            else
                if (a && (b == 0 || Y2[p] - Y2[a] < Y2[p] - Y2[b]))
                    Anc[0][p] = a, Sum[0][p] = (Y2[p] - Y2[a]) + Abs(X2[p] - X2[a]);
                else
                    Anc[0][p] = b, Sum[0][p] = Y2[p] - Y2[b];
        }
        else
        {
            if (a == 0 && b == 0)
                Y2[p] = max(0LL, Y2[p] - T[p]), T[p] = 0LL;
            else
                if (a && (b == 0 || Y2[p] - Y2[a] < Y2[p] - Y2[b]))
                    if (T[p] <= Y2[p] - Y2[a])
                        Y2[p] -= T[p], T[p] = 0LL;
                    else
                    {
                        T[p] -= Y2[p] - Y2[a], Y2[p] = Y2[a];
                        if (T[p] <= Abs(X2[p] - X2[a]))
                        {
                            if (X2[a] <= X2[p])
                                X2[p] -= T[p];
                            else
                                X2[p] += T[p];
                            T[p] = 0LL;
                        }
                        else
                            T[p] -= Abs(X2[p] - X2[a]), X2[p] = a;
                    }
                else
                    if (T[p] <= Abs(Y2[p] - Y2[b]))
                    {
                        if (Y2[b] <= Y2[p])
                            Y2[p] -= T[p];
                        else
                            Y2[p] += T[p];
                        T[p] = 0LL;
                    }
                    else
                        T[p] -= Abs(Y2[p] - Y2[b]), X2[p] = b;
        }
    }
}

inline int getU(const int &x)
{
    return max(Y1[x], Y2[x]);
}

inline bool compU(const int &a, const int &b)
{
    return getU(a) > getU(b);
}

void goU()
{
    build_tree(1, 0, M), memset(C, 0, sizeof(C));
    sort(L + 1, L + 1 + L[0], compU);
    sort(R + 1, R + 1 + R[0], compU);
    sort(D + 1, D + 1 + D[0], compU);
    sort(U + 1, U + 1 + U[0], compU);
    for (int l = 1, r = 1, d = 1, u = 1, a, b, p;u <= U[0];++u)
    {
        p = U[u];
        while (d <= D[0] && getU(D[d]) >= getU(p))
        {
            if (D[d] <= N)
                C[X2[D[d]]] = D[d];
            ++d;
        }
        while ((l <= L[0] && getU(L[l]) >= getU(p)) || (r <= R[0] && getU(R[r]) >= getU(p)))
            if ((l <= L[0]) && (r > R[0] || getU(L[l]) >= getU(R[r])))
            {
                if (L[l] <= N)
                    cover(1, X2[L[l]], X1[L[l]], L[l]);
                ++l;
            }
            else
            {
                if (R[r] <= N)
                    cover(1, X1[R[r]], X2[R[r]], R[r]);
                ++r;
            }
        a = query(1, X2[p]), b = C[X2[p]];
        if (p <= N)
        {
            if (a == 0 && b == 0)
                Anc[0][p] = -1;
            else
                if (a && (b == 0 || Y2[a] - Y2[p] < Y2[b] - Y2[p]))
                    Anc[0][p] = a, Sum[0][p] = (Y2[a] - Y2[p]) + Abs(X2[p] - X2[a]);
                else
                    Anc[0][p] = b, Sum[0][p] = Y2[b] - Y2[p];
        }
        else
        {
            if (a == 0 && b == 0)
                Y2[p] = min(M * 1LL, Y2[p] + T[p]), T[p] = 0LL;
            else
                if (a && (b == 0 || Y2[a] - Y2[p] < Y2[b] - Y2[p]))
                    if (T[p] <= Y2[a] - Y2[p])
                        Y2[p] += T[p], T[p] = 0LL;
                    else
                    {
                        T[p] -= Y2[a] - Y2[p], Y2[p] = Y2[a];
                        if (T[p] <= Abs(X2[p] - X2[a]))
                        {
                            if (X2[a] <= X2[p])
                                X2[p] -= T[p];
                            else
                                X2[p] += T[p];
                            T[p] = 0LL;
                        }
                        else
                            T[p] -= Abs(X2[p] - X2[a]), X2[p] = a;
                    }
                else
                    if (T[p] <= Abs(Y2[b] - Y2[p]))
                    {
                        if (Y2[b] <= Y2[p])
                            Y2[p] -= T[p];
                        else
                            Y2[p] += T[p];
                        T[p] = 0LL;
                    }
                    else
                        T[p] -= Abs(Y2[b] - Y2[p]), X2[p] = b;
        }
    }
}

void get(const int &i, const int &u)
{
    if (X2[u] < X1[u])
        X2[i] = max(0LL, X2[i] - T[i]);
    if (X2[u] > X1[u])
        X2[i] = min(M * 1LL, X2[i] + T[i]);
    if (Y2[u] < Y1[u])
        Y2[i] = max(0LL, Y2[i] - T[i]);
    if (Y2[u] > Y1[u])
        Y2[i] = min(M * 1LL, Y2[i] + T[i]);
}

int main()
{

    gi(N), gi(M);
    for (int i = 1;i <= N;++i)
    {
        gi(X1[i]), gi(Y1[i]), gi(X2[i]), gi(Y2[i]);
        if (X2[i] < X1[i])
            L[++L[0]] = i;
        if (X2[i] > X1[i])
            R[++R[0]] = i;
        if (Y2[i] < Y1[i])
            D[++D[0]] = i;
        if (Y2[i] > Y1[i])
            U[++U[0]] = i;
    }
    gi(Q);
    for (int i = 1;i <= Q;++i)
    {
        gi(X2[N + i]), gi(Y2[N + i]), X1[N + i] = X2[N + i], Y1[N + i] = Y2[N + i];
        char op[5];
        scanf("%s", op);
        if (*op == 'L')
            L[++L[0]] = N + i;
        if (*op == 'R')
            R[++R[0]] = N + i;
        if (*op == 'D')
            D[++D[0]] = N + i;
        if (*op == 'U')
            U[++U[0]] = N + i;
        gi(T[N + i]);
    }
    goL(), goR(), goD(), goU();
    for (int j = 1;j <= 59;++j)
        for (int i = 1;i <= N;++i)
            if (Anc[j - 1][i] == -1)
                Anc[j][i] = -1;
            else
            {
                Anc[j][i] = Anc[j - 1][Anc[j - 1][i]];
                Sum[j][i] = Sum[j - 1][i] + Sum[j - 1][Anc[j - 1][i]];
                Sum[j][i] = min(Sum[j][i], 1000000000000000LL + 1LL);
            }
    for (int i = N + 1, u;i <= N + Q;++i)
    {
        if (T[i])
        {
            u = X2[i];
            for (int j = 59;j >= 0;--j)
                if (Anc[j][u] != -1 && Sum[j][u] <= T[i])
                    T[i] -= Sum[j][u], u = Anc[j][u];
            X2[i] = X2[u], Y2[i] = Y2[u];
            if (Anc[0][u] == -1)
                get(i, u);
            else
            {
                if (X2[u] < X1[u])
                    if (T[i] <= X2[i] - X2[Anc[0][u]])
                        get(i, u);
                    else
                        T[i] -= X2[i] - X2[Anc[0][u]], X2[i] = X2[Anc[0][u]], get(i, Anc[0][u]);
                if (X2[u] > X1[u])
                    if (T[i] <= X2[Anc[0][u]] - X2[i])
                        get(i, u);
                    else
                        T[i] -= X2[Anc[0][u]] - X2[i], X2[i] = X2[Anc[0][u]], get(i, Anc[0][u]);
                if (Y2[u] < Y1[u])
                    if (T[i] <= Y2[i] - Y2[Anc[0][u]])
                        get(i, u);
                    else
                        T[i] -= Y2[i] - Y2[Anc[0][u]], Y2[i] = Y2[Anc[0][u]], get(i, Anc[0][u]);
                if (Y2[u] > Y1[u])
                    if (T[i] <= Y2[Anc[0][u]] - Y2[i])
                        get(i, u);
                    else
                        T[i] -= Y2[Anc[0][u]] - Y2[i], Y2[i] = Y2[Anc[0][u]], get(i, Anc[0][u]);
            }
        }
        printf("%d %d
", X2[i], Y2[i]);
    }
    return 0;