1、背景
有了强大的log-linear模型，连水槽都能拿来做分类特征了，当然要想办法用一下试试了。log-linear模型的输入是一系列几乎接近自然语言的特征方程，这种抽象的东西拿来做语义识别自然是再好不过了。语义识别有一个重要的步骤，叫做 ”给句子贴标签“，简而言之，就是给定一个句子，通过识别其中一些特征：比如存在人名，地名，日期，商品名称，从而判断这个句子的属性（做交易，下任务，更改设置等。） 能够准确的识别句子中的这些 tag 可以有助于理解一个句子。但是要怎样来确定某个单词是不是地名或者人名呢？光靠首字母是否大小写或者和对应的库去匹配显然是不够好的。
为了更好的完成任务，引入上下文成了一个有意义的手段。对自然语言或者大部分信号而言，在某信号之前的上个信号有着重要的意义（比如我使用了重要的，那么下个词多半是名词）。所以构建了以相邻信号作为特征方程的模型，成为条件随机场。
普通的log-linear模型长这样：
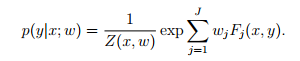
如果把上下文考虑进特征方程，那么它的特征方程大概长这样：
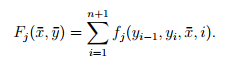
(x-) 代表整个句子，(y-)代表标签序列。一个n个词（x的长度）的句子显然有m个标签（tag的容量）。因为句子的长度一般都不同，但“标签”的集合却可以是相同的（词性总归就那么几个），所以，我们需要恒定数目的特征方程（一般情况下特征方程的数目是m*n).
故考虑设计了上述形式的子特征方程，以 y_i-1 （这表示某标签序列的第i-1个标签）以及第i个标签形成的子特征方程遍历整个句子。最后将子特征方程遍历的结果求和，作为总特征方程的返回值。子特征方程可以是以下形式（如果符合则返回1，否则返回0）
f1.前面为名词，则后面一个词开头为M
f2.前面为副词，则后面一个词是形容词
f3.前面为形容词，则后面一个词以y结尾
...
显然对于一般情况下的句子而言，上述子特征方程求和后会给 F_j 一个比较大的值（因为符合语法规则）。注意每个 f_ 里都只能有两个词性。当我们有很多这样的规则时，正确的规则（名次后面接动词）会被训练成较高的权重，而错误的规则则会被赋予较低的权重，最后得到的词性序列会有较高的正确性。
2、CRF 模型的数学分析
拿到CRF模型后，我们要想办法能够通过训练得到 一组合适的参数w_j，以实现分类器的构造。但是在拿到参数之前，还是需要做些准备工作，比如：获得各阶导数的表达式。ok，由于我们引入了 子特征方程 f_ 并且 F_与f_ 存在求和关系，所以这里的算法会比较复杂。
整体的表达式长这样：
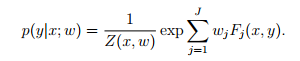
如果把 f_j 带入，表达式长这样：
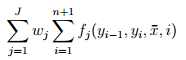（外围部分被忽略了）
最终目标也就变成了：
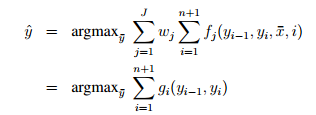
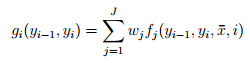
这里做了一个乘法结合律，把wj和fj放在了一起，总结成了一个g函数。是不是 “一个” g函数呢？这倒是不一定。。。。。。。
对于任意一个 i ，gi 都是不同的方程。和 gi 有关的参数是两个，这两个参数都是tag。那么假设 tag的集合里有m个元素，则gi的总个数是 m^2（所有的tag组合都要遍历）。也就是说，对长度为n的一个句子，都要算 n*m^2 次（此处可能有误）。。。。
计算次数这么多显然有点问题。故考虑设计一种递归的算法，来减小计算的规模。这里不详细讲述。
3.模型迭代所使用的梯度
要对 log-linear 模型进行标定，当然是要想办法使模型参数最符合训练集合了。最符合训练集合的意思就是要想办法使得在某组参数下，训练集发生的概率达到最大。不妨对概率取对数，使得式子线性化。
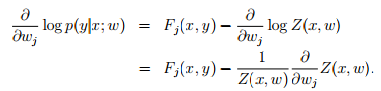
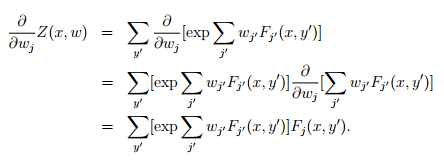
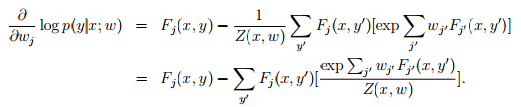
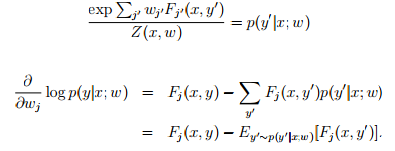
ok，到此为止，已经求出了各个参数导数的表达形式，F_j(x,y)是很容易求的，对任意训练集这都是已知的。而后面的E求起来却比较麻烦，它需要把所有可行的标签带入Fj中，并且乘以p(这里p也好求，给定wj，p就是已知的）但是这样子梯度的计算量就非常大。相当于每一次迭代都需要对 标签集 进行遍历，计算量很大，不过机智的计算机科学家设计了算法通过预测p的分布，来描述E。具体的算法不再赘述，总之，条件随机场模型是一种可考虑多因素，对物体进行多标签分类的模型。其训练过程需要有监督学习，对机器人视觉来说，有监督学习并不是一件简单的事情。物体的外形也很难和物体的标签联系起来（圆的是杯子还是茶叶罐？）所以条件随机场对计算机视觉会更有效，基于纹理颜色形状等信息的二维图像更适合去探究其意义。