概率图模型G(V,E)由节点V和边E构成。在之前马尔科夫模型相关的博客中，我谈到马尔科夫模型的本质是当两个人交流后，其意见（两个随机变量）同意0与不同意1的概率组合。而势函数表达的是两个意见相同或者相左的程度。
我们搞的那么麻烦，最后想要得到的不就是每个意见正确与否（随机变量取不同值的概率）吗？与其采用解析的方法去算，去把所有其他的变量边际掉，那干脆采用模拟的方法，让这个消息传递跑起来，把系统迭代N次以后的结果拿出来分析。这种朴素（Naive）的想法，就是 Message Passing 算法。
1. 聚类图
在执行消息传递之前，我们需要指定两件事情：1.掌握消息的人有哪些，手里都有哪些消息。2.他把这个消息告诉了谁。为了解答这两个问题，需要从我们手里仅有的材料去构造。
P(ABCD) = P(AB)*P(BC)*P(CD)*P(DA) ------- 这里的P是未归一化的概率。 通过这个联合概率计算式，我们获得一种叫做聚类图的全新图模型。从概率图到聚类图如下所示。
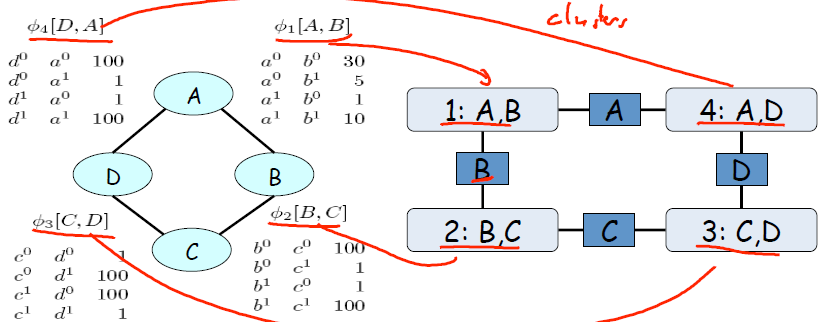
其中，聚类图中存在 Cluster 和 Edge. Cluster 就是掌握消息的人，Cluster 里的内容就是人所掌握的消息。Edge 连接了两个交互消息的人，Edge上是两个人交换的消息。当然，聚类图不仅仅是这么简单的结构。还有更复杂的聚类图如下.
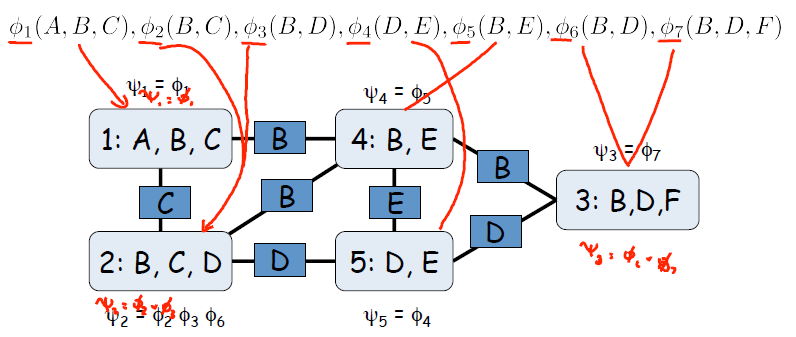
势函数表达的是两个人意见相同或者相左的程度，两个势函数相乘则会表达多个消息相同或相左的程度。多个势函数相乘可以成为某个人的消息函数。
对于聚类图，有以下性质：
1.C(Clusters)由节点组成。2. 边上传递的消息，是两个C的交集（必须要两个人同时知道的消息才能交流）。3.消息函数是势函数的乘积。
总结一下：消息是随机变量，并且都是相关的。人掌握消息之间的关系。人和人之间可以传递消息。
我们假设消息A:明天下雨 B:明天下雪 C:地上有水 那么人们一般都会认为 A1B1C1的可能性肯定大于A1B1C0。而E有可能是明天有洒水车。总之，不同的人掌握着不同的消息。消息与消息之间会相互影响。
2.消息传递
有了消息之后，两个都知道同一件事情的人就会交流和这件事有关的内容，比如 2 会告诉 1 关于C(地上有没有水)的事情，这会改变1对消息C的看法（概率）。我们把消息传递写成以下形式。
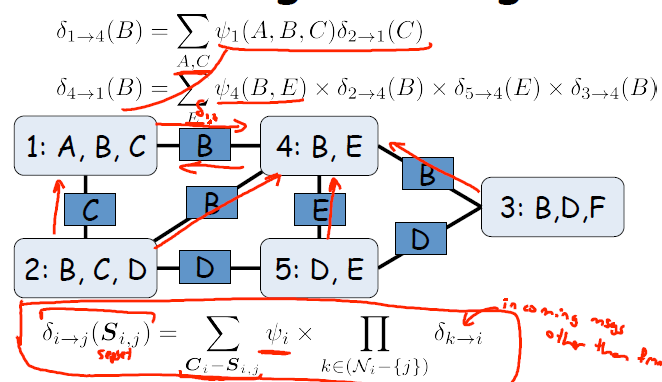
i->j 表示消息从 i 传递到 j。Sij表示被传递的消息。通式的物理意义有以下三点：
1.消息从 i 传递到 j， i 会综合所有人给他说的信息（把所有的δ 相乘）
2.加上自己对消息组合的认知（把 δ 相乘 的结果乘以消息之间的关系）
3.去除掉不需要传递的部分 （把其他变量边际掉）
以上循环一定次数后，达到某种稳定状态。
最终计算某个人对所有消息的看法Belief （所有稳态输入消息δ 乘以消息关系）
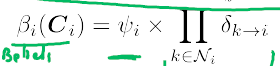
这种算法会和精确解法存在一定偏差，故此仅为一种近似算法。
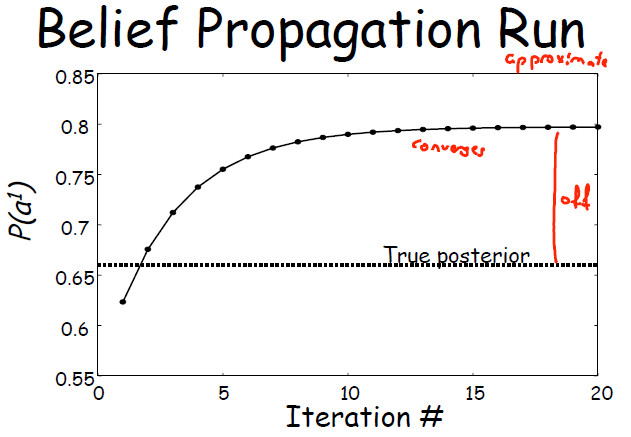
3.聚类图的性质
不是随便一幅图都可以作为聚类图。聚类图有3个基本要素：
1.每个势函数都被使用，且被使用一次。
2.聚类图中消息传递不能形成环。
3.每个消息如果存在两个知道的人，这两个人必须要有交流途径
关于第一点，势函数描述了消息之间的关系，如果漏了，则失去了消息之间的某个信息，如果重复使用，则某种关系被多余的加强了。
第二点则比较有意思，其实际上描述的是一个正反馈的情况。假设有个人，编了一个谎话：明天会下雨。并且把这个谎话告诉了A，然后A又告诉B，B->C,C-D。如果恰好编这个谎话的人正好和D认识，又正好交流了明天是否会下雨的情况。那么就“谎话到最后自己都信了”。这就对“明天下雨”这个随机变量的概率产生较大的估计偏差。简而言之就是，消息不能成环。
第三点要表达的是，如果甲乙两个人都知道一件事情A，那么他们一定要有交流途径，无论直接交流还是通过其他人转达，总之消息A一定要有在甲乙两人之间联通的路径。
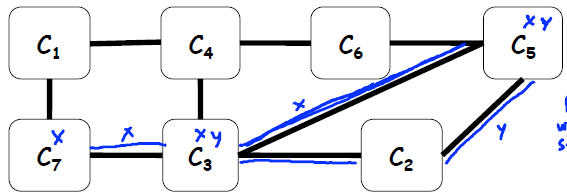
值得注意的一点是，明天下雨A和地上有水C之间可能存在较强的相关性，就算A没有形成环，却通过C形成了环，最终也会对结果产生较大影响。比如图中，xy强相关时，消息传递算法的表现并不好。
有一种一定能够满足上诉性质的聚类图成为Bethe Clusters Graph。在使用消息传递算法时，优先考虑构造此聚类图。该聚类图中有两种不同的人，一种掌握多个消息，一种掌握单种消息。这样的聚类图一定不会存在环。其形式如下所示:
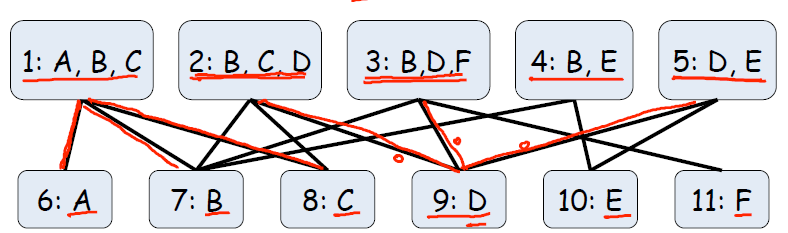
4. 传播算法的性质
一群人交换意见，如果大家最后意见都相同了。比如 甲乙都认为明天下雨的概率是0.6，乙丙都认为明天地上有水的概率是0.7.........这种情况称为聚类图校准了。
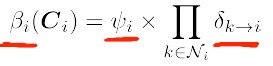
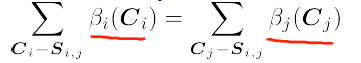
公式表示，边际掉无关量，两个人对交流消息的看法是一致的。
意见相同还有一个说法，就是交流过程稳定，也就是说，在经过无数次迭代后，消息收敛了。
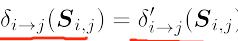
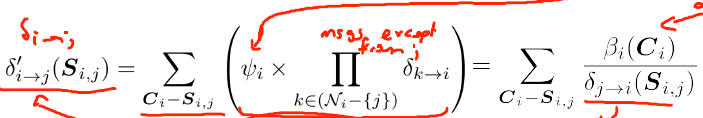——————消息传递公式
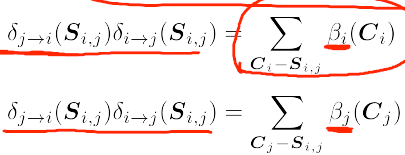————————δj-i与求和无关，因为不在求和域内，故可以乘出去。发现i,j是对称轮换的
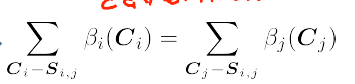——————————最终得出收敛和校准是等价的
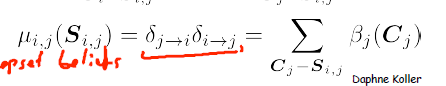——————————一种新的符号
————此式证明了，消息传递算法无论如何运行，初始设定都没有引入新的信息
5.总结
消息传递算法是一种朴素的模拟推断算法，用于求解随机变量的给定依赖条件下的概率。这种算法的计算结果是有偏的，但该算法却可以大幅降低推断所需要的计算量。