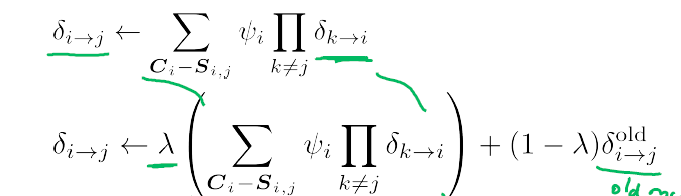在之前的消息传递算法中,谈到了聚类图模型的一些性质。其中就有消息不能形成闭环,否则会导致“假消息传到最后我自己都信了”。为了解决这种问题,引入了一种称为团树(clique tree)的数据结构,树模型没有图模型中的环,所以此模型要比图模型更健壮,更容易收敛。
1.团树模型
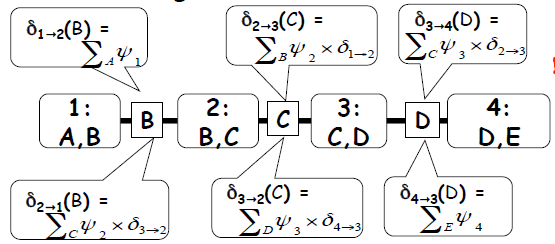
链模型是一种最简单的树模型,其结构如下图所示,假设信息从最左端传入则有以下式子。
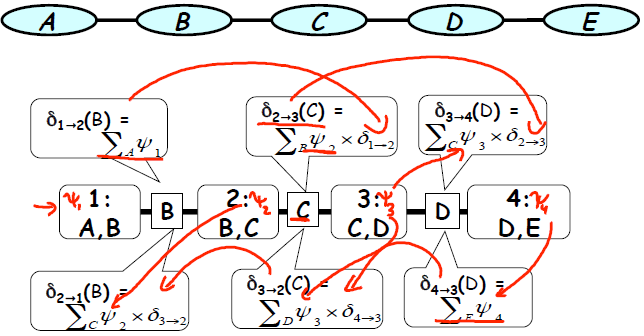
假设要对变量 CD 进行推断,则应该求 Belief(3) = deta 2->3 *deta 4->3 * phi(3).
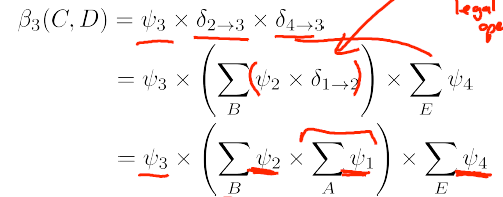
从这里可以看出,团树算法是一种精确推断算法。它和变量消除算法在理论推导上是等价的。
上面的例子只是一种非常简单的团树,团树的本质还是聚类图,只不过是一种特殊的聚类图。对于更一般的概率图,也可以生成团树图。
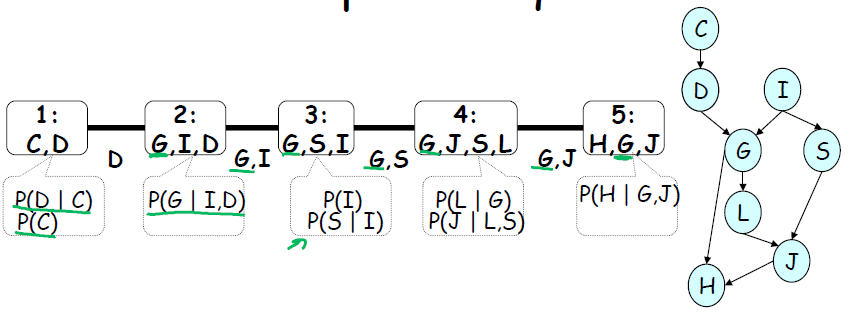
其中,每个cluster都是变量消除诱导图中的一个最小map。
2.团树模型的计算
从上面分析可知,团树模型本质上和变量消除算法还有说不清道不明的关系(团树模型也是精确推理模型)。但是这个算法的优势在于,它可以利用消息传递机制达到收敛。之前提过,聚类图模型中的收敛指的是消息不变。除此之外,聚类图的本质是一种数据结构,它可以储存很多中间计算结果。如果我们有很多变量 ABCDEF,那么我们想知道P(A),则需要执行一次变量消除。如果要计算P(B)又要执行一次变量消除。如果中途得到了某个变量的观测,又会对算法全局产生影响。但是使用团树模型可以巧妙的避免这些问题。
首先,一旦模型迭代收敛之后。所有的消息都是不变的,每个消息都是可以被读取的。
每个团的belief,实际上就是未归一划的联合概率,要算单个变量的概率,只需要把其他的变量边际掉就行。这样一来,只需要一次迭代收敛,每个变量的概率都是可算的。并且算起来方便。
其次,如果对模型引入先验知识比如 A = a 时, 我们需要对 D 的概率进行估计。按照变量消除的思路又要从头来一次。但是如果使用团树结构则不用,因为 A的取值只影响 deta1->2以及左向传递的消息,对右向传递的消息则毫无影响,可以保留原先对右向传递消息的计算值,只重新计算左向传递结果即可。
总而言之,使用团树算法相对于变量消除算法,可以大幅降低计算规模,也便于对任意一个随机变量进行查询。
3.团树算法与独立性
聚类图是由概率图分析得到的。同样,聚类图中也继承了概率图在独立性方面的某些特性。团树图有以下性质:
如果能观测到edge上的变量,则edge两端的变量的独立的。
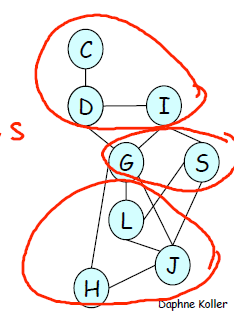
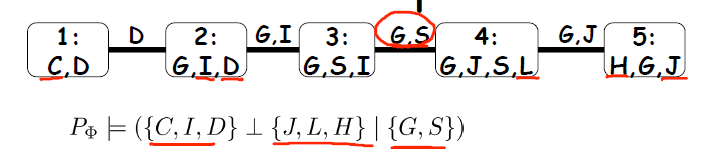
显然,如果给定 GS , CDI 与 HJL 就是独立的。
4.团树算法与VE算法的联系
之前提到团树算法和VE算法都是精确推理的算法。本质上他们之间存在对应关系。
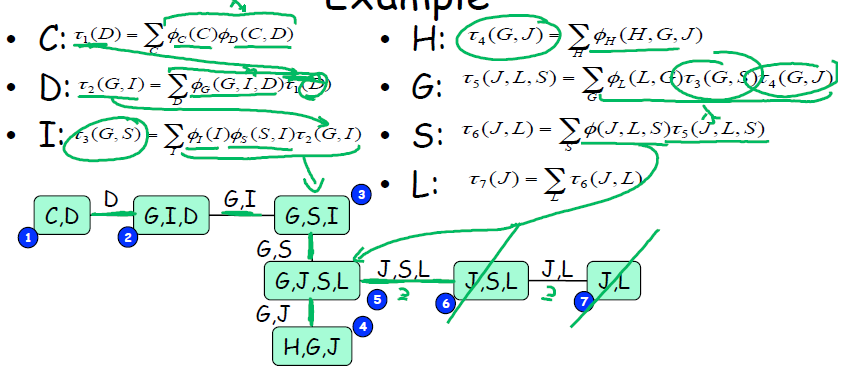
1.团树传递的消息实际上是两个cluster之间共同变量。从1 - > 2 消除了1 中2 不包含的变量。这与VE算法中把 势函数边际成 τ 是一样的。也就是说 deta ---> tau.
2.团树的cluster 是多个 phi相乘得到的。多个phi相乘是VE算法构造初始的因子相乘。
利用团树算法和VE算法之间的关系,我们可以利用模拟VE算法运行,来生成团树图。也就是说,假设我在执行VE算法(顺序由概率图决定),用VE算法生成团树图,再利用团树结构简化VE的计算,最终达到变量推断的目的。图中显示了一个简单的例子。
5.实际置信传播算法的操作
在之前的分析中,我们已经得到了消息传递算法的性质,执行机制等。但是如果把它编程成代码的时候,我们会遇到以下几个问题:
1.如果cluster很多,我每次只传递一条消息,那么大部分节点都处于无所事事状态,这样好么
2.迭代一定次数以后一定会收敛吗
3.收敛了结果一定对吗
4.怎样才能尽可能收敛
针对第一个问题,计算机科学家采用的往往是并行消息传递,并行消息传递又分同时传递与非对称传递(主要针对网格聚类图),结果是非同时传递的效果往往更好。此外,还可以在图中选出一棵团树,尽量在这棵团树上达到收敛,以保证尽可能多的节点收敛。本身只有形成环的时候才会不收敛。
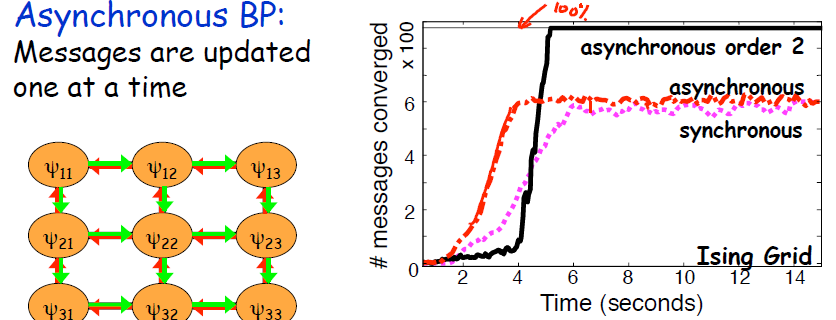
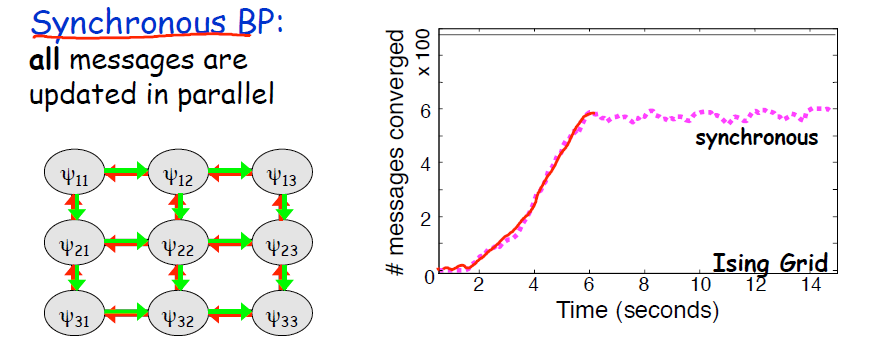
第二个问题,是不是一定会收敛,答案是不是的,奇怪的是有些消息会收敛,有些消息却不会。实际上在传递的过程中,有些消息已经达成平衡,在平衡状态下和其他不收敛的消息解耦了。此外,消息传递顺序对收敛性影响也很大。
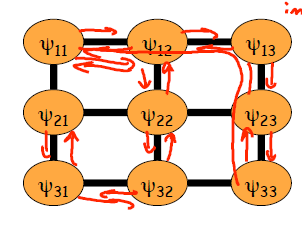
第三个问题,结果不一定对。本来这就是蒙特卡洛算法,不能保证一定收敛到正确值。
第四个问题,增加阻尼可以增加收敛的可能性,简而言之,就是把之前的值考虑进去,让下一个值和之前的值尽可能靠近。把新的值”拖住“。